Primjer 1 Zadana funkcija f(x) = 3x 2 + 4x– 5. Napišimo jednadžbu tangente na graf funkcije f(x) u točki grafa s apscisom x 0 = 1.

Odluka. Derivat funkcije f(x) postoji za bilo koji x R . Nađimo ga:

= (3x 2 + 4x– 5)′ = 6 x + 4.

Zatim f(x 0) = f(1) = 2; (x 0) = = 10. Tangentna jednadžba ima oblik:

y = (x 0) (x – x 0) + f(x 0),

y = 10(x – 1) + 2,

y = 10x – 8.

Odgovor. y = 10x – 8.

Primjer 2 Zadana funkcija f(x) = x 3 – 3x 2 + 2x+ 5. Napišimo jednadžbu tangente na graf funkcije f(x), paralelno s pravom y = 2x – 11.

Odluka. Derivat funkcije f(x) postoji za bilo koji x R . Nađimo ga:

= (x 3 – 3x 2 + 2x+ 5)′ = 3 x 2 – 6x + 2.

Budući da je tangenta na graf funkcije f(x) u točki s apscisom x 0 je paralelno s pravom y = 2x– 11, tada je njegov nagib 2, tj. ( x 0) = 2. Nađi ovu apscisu iz uvjeta da je 3 x– 6x 0 + 2 = 2. Ova jednakost vrijedi samo za x 0 = 0 i x 0 = 2. Budući da u oba slučaja f(x 0) = 5, zatim pravac y = 2x + b dodiruje graf funkcije ili u točki (0; 5) ili u točki (2; 5).

U prvom slučaju vrijedi numerička jednakost 5 = 2×0 + b, gdje b= 5, au drugom slučaju brojčana jednakost vrijedi 5 = 2 × 2 + b, gdje b = 1.

Dakle, postoje dvije tangente y = 2x+ 5 i y = 2x+ 1 na graf funkcije f(x) paralelno s pravom y = 2x – 11.

Odgovor. y = 2x + 5, y = 2x + 1.

Primjer 3 Zadana funkcija f(x) = x 2 – 6x+ 7. Napišimo jednadžbu tangente na graf funkcije f(x) prolazeći kroz točku A (2; –5).

Odluka. Kao f(2) –5, zatim točka A ne pripada grafu funkcije f(x). Neka bude x 0 - apscisa dodirne točke.

Derivat funkcije f(x) postoji za bilo koji x R . Nađimo ga:

= (x 2 – 6x+ 1)′ = 2 x – 6.

Zatim f(x 0) = x– 6x 0 + 7; (x 0) = 2x 0 - 6. Tangentna jednadžba ima oblik:

y = (2x 0 – 6)(x – x 0) + x– 6x+ 7,

y = (2x 0 – 6)x– x+ 7.

Od točke A pripada tangenti, tada je brojčana jednakost istinita

–5 = (2x 0 – 6)×2– x+ 7,

gdje x 0 = 0 ili x 0 = 4. To znači da kroz točku A moguće je nacrtati dvije tangente na graf funkcije f(x).

Ako je a x 0 = 0, tada tangentna jednadžba ima oblik y = –6x+ 7. Ako x 0 = 4, tada tangentna jednadžba ima oblik y = 2x – 9.

Odgovor. y = –6x + 7, y = 2x – 9.

Primjer 4 Zadane funkcije f(x) = x 2 – 2x+ 2 i g(x) = –x 2 - 3. Napišimo jednadžbu zajedničke tangente na grafove ovih funkcija.

Odluka. Neka bude x 1 - apscisa dodirne točke željene linije s grafom funkcije f(x), a x 2 - apscisa dodirne točke istog pravca s grafom funkcije g(x).

Derivat funkcije f(x) postoji za bilo koji x R . Nađimo ga:

= (x 2 – 2x+ 2)′ = 2 x – 2.

Zatim f(x 1) = x– 2x 1 + 2; (x 1) = 2x 1 - 2. Tangentna jednadžba ima oblik:

y = (2x 1 – 2)(x – x 1) + x– 2x 1 + 2,

y = (2x 1 – 2)x – x+ 2. (1)

Nađimo derivaciju funkcije g(x):

= (–x 2 – 3)′ = –2 x.

U članku se detaljno objašnjavaju definicije, geometrijsko značenje izvedenice s grafičke oznake. Na primjerima će se razmotriti jednadžba tangente, naći će se jednadžbe tangente na krivulje 2. reda.

Yandex.RTB R-A-339285-1 Definicija 1

Kut nagiba ravne crte y \u003d k x + b naziva se kut α, koji se mjeri od pozitivnog smjera osi x do ravne crte y = k x + b u pozitivnom smjeru.

Na slici je smjer vola označen zelenom strelicom i zelenim lukom, a kut nagiba crvenim lukom. Plava linija se odnosi na ravnu liniju.

Definicija 2

Nagib ravne crte y \u003d k x + b naziva se numerički koeficijent k.

Nagib je jednak nagibu ravne, drugim riječima k = t g α .

• Kut nagiba ravne je 0 samo ako je o x paralelan, a nagib je nula, jer je tangent nule 0. Dakle, oblik jednadžbe će biti y = b.
• Ako je kut nagiba ravne y = k x + b oštar, tada su uvjeti 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение nagib k se smatra pozitivnim brojem, jer vrijednost tangente zadovoljava uvjet t g α > 0, a graf se povećava.
• Ako je α \u003d π 2, tada je mjesto pravca okomito na x. Jednakost je određena jednakošću x = c pri čemu je vrijednost c realan broj.
• Ako je kut nagiba ravne y = k x + b tup, onda odgovara uvjetima π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает negativno značenje, a graf se smanjuje.

Definicija 3

Sekansa je pravac koja prolazi kroz 2 točke funkcije f (x). Drugim riječima, sekansa je ravna crta koja prolazi kroz bilo koje dvije točke na grafu zadane funkcije.

Slika pokazuje da je A B sekansa, a f (x) crna krivulja, α crveni luk, koji označava kut nagiba sekante.

Kada je nagib ravne crte jednak tangenti kuta nagiba, jasno je da se tangenta iz pravokutnog trokuta A B C može naći u odnosu na suprotni krak susjednom.

Definicija 4

Dobivamo formulu za pronalaženje sekansa oblika:

k = t g α = B C A C = f (x B) - f x A x B - x A , gdje su apscise točaka A i B vrijednosti x A , x B i f (x A) , f (x B) su funkcije vrijednosti u tim točkama.

Očito je nagib sekante definiran pomoću jednakosti k \u003d f (x B) - f (x A) x B - x A ili k \u003d f (x A) - f (x B) x A - x B, a jednadžba se mora napisati kao y = f (x B) - f (x A) x B - x A x - x A + f (x A) ili
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekanta vizualno dijeli graf na 3 dijela: lijevo od točke A, od A do B, desno od B. Slika ispod pokazuje da postoje tri sekante koje se smatraju istim, tj. postaviti pomoću slične jednadžbe.

Po definiciji je jasno da se pravac i njezin sekans u ovom slučaju podudaraju.

Sekansa može više puta presijecati graf zadane funkcije. Ako postoji jednadžba oblika y \u003d 0 za sekantu, tada je broj točaka presjeka sa sinusoidom beskonačan.

Definicija 5

Tangenta na graf funkcije f (x) u točki x 0 ; f (x 0) naziva se ravna linija koja prolazi kroz danu točku x 0; f (x 0) , uz prisutnost segmenta koji ima mnogo x vrijednosti blizu x 0 .

Primjer 1

Pogledajmo pobliže primjer u nastavku. Tada se može vidjeti da se pravac zadana funkcijom y = x + 1 smatra tangentom na y = 2 x u točki s koordinatama (1 ; 2). Radi jasnoće, potrebno je razmotriti grafove s vrijednostima bliskim (1; 2). Funkcija y = 2 x označena je crnom bojom, plava linija je tangenta, crvena točka je točka presjeka.

Očito, y = 2 x spaja se s linijom y = x + 1.

Da bismo odredili tangentu, treba razmotriti ponašanje tangente A B dok se točka B beskonačno približava točki A. Radi jasnoće predstavljamo sliku.

Sekansa A B, označena plavom linijom, teži položaju same tangente, a kut nagiba sekante α počet će težiti kutu nagiba same tangente α x.

Definicija 6

Tangenta na graf funkcije y \u003d f (x) u točki A je granični položaj sekante A B u B koja teži A, odnosno B → A.

Sada prelazimo na razmatranje geometrijskog značenja derivacije funkcije u točki.

Prijeđimo na razmatranje sekante A B za funkciju f (x), gdje su A i B s koordinatama x 0, f (x 0) i x 0 + ∆ x, f (x 0 + ∆ x), i ∆ x se označava kao prirast argumenta. Sada će funkcija poprimiti oblik ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Radi jasnoće, uzmimo sliku kao primjer.

Razmotrite rezultat pravokutni trokut A B C. Za rješenje koristimo definiciju tangente, odnosno dobivamo omjer ∆ y ∆ x = t g α . Iz definicije tangente slijedi da je lim ∆ x → 0 ∆ y ∆ x = t g α x . Prema pravilu derivacije u točki, imamo da se derivacija f (x) u točki x 0 naziva granicom omjera prirasta funkcije i prirasta argumenta, gdje je ∆ x → 0, tada označeno kao f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Iz toga slijedi da je f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, gdje je k x označen kao nagib tangente.

To jest, dobivamo da f ' (x) može postojati u točki x 0 i, poput tangente na zadani graf funkcije u točki dodira jednakoj x 0 , f 0 (x 0) , gdje je vrijednost nagiba tangente u točki jednaka je derivaciji u točki x 0 . Tada dobivamo da je k x = f "(x 0) .

Geometrijsko značenje derivacije funkcije u točki je da je dan koncept postojanja tangente na graf u istoj točki.

Za pisanje jednadžbe bilo koje ravne linije u ravnini potrebno je imati nagib s točkom kroz koju ona prolazi. Njegova oznaka se uzima kao x 0 na raskrižju.

Jednadžba tangente na graf funkcije y \u003d f (x) u točki x 0, f 0 (x 0) ima oblik y \u003d f "(x 0) x - x 0 + f (x 0) .

To znači da konačna vrijednost derivacije f"(x 0) može odrediti položaj tangente, odnosno okomito pod uvjetom lim x → x 0 + 0 f" (x) = ∞ i lim x → x 0 - 0 f "(x ) = ∞ ili odsutnost uopće pod uvjetom lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) .

Položaj tangente ovisi o vrijednosti njenog nagiba k x \u003d f "(x 0). Kada je paralelno s osi o x, dobivamo da je k k = 0, kada je paralelno s o y - k x \u003d ∞, a oblik tangentne jednadžbe x \u003d x 0 raste s k x > 0 , smanjuje se kao k x< 0 .

Primjer 2

Sastavite jednadžbu tangente na graf funkcije y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 u točki s koordinatama (1; 3) s definicijom kuta nagib.

Odluka

Prema pretpostavci, imamo da je funkcija definirana za sve realni brojevi. Dobivamo da je točka s koordinatama određenim uvjetom (1; 3) dodirna točka, tada je x 0 = - 1 , f (x 0) = - 3 .

Potrebno je pronaći derivaciju u točki s vrijednošću - 1 . Shvaćamo to

y "= e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" = = e x + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = e x + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Vrijednost f’ (x) u točki dodira je nagib tangente, koji je jednak tangentu nagiba.

Tada je k x = t g α x = y "(x 0) = 3 3

Slijedi da je α x = a r c t g 3 3 = π 6

Odgovor: tangentna jednadžba poprima oblik

y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

Radi jasnoće dajemo primjer na grafičkoj ilustraciji.

Crna boja se koristi za prikaz izvorne funkcije, plava boja- slika tangente, crvena točka - dodirna točka. Slika s desne strane prikazuje uvećani prikaz.

Primjer 3

Saznati postojanje tangente na graf zadane funkcije
y = 3 x - 1 5 + 1 u točki s koordinatama (1 ; 1) . Napišite jednadžbu i odredite kut nagiba.

Odluka

Pod pretpostavkom imamo da je domena zadane funkcije skup svih realnih brojeva.

Prijeđimo na traženje izvedenice

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Ako je x 0 = 1 , tada f ' (x) nije definirano, ali su granice zapisane kao lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ i lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , što znači postojanje vertikalne tangente na točka (1; 1) .

Odgovor: jednadžba će imati oblik x \u003d 1, gdje će kut nagiba biti jednak π 2.

Nacrtajmo ga grafikonom radi jasnoće.

Primjer 4

Pronađite točke grafa funkcija y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , gdje je

1. Tangenta ne postoji;
2. Tangenta je paralelna s x;
3. Tangenta je paralelna s pravcem y = 8 5 x + 4 .

Odluka

Potrebno je obratiti pozornost na domenu definicije. Pod pretpostavkom imamo da je funkcija definirana na skupu svih realnih brojeva. Proširite modul i riješite sustav s intervalima x ∈ - ∞ ; 2 i [-2; +∞) . Shvaćamo to

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

Funkciju treba razlikovati. mi to imamo

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

Kada je x = - 2, tada derivacija ne postoji jer jednostrane granice nisu jednake u toj točki:

lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Izračunavamo vrijednost funkcije u točki x \u003d - 2, gdje to dobivamo

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, odnosno tangenta na točka (- 2; - 2) neće postojati.
2. Tangenta je paralelna s x kada je nagib nula. Tada je k x \u003d t g α x \u003d f "(x 0). To jest, potrebno je pronaći vrijednosti takvog x kada ga derivacija funkcije okrene na nulu. To jest, vrijednosti f '(x) i bit će dodirne točke, gdje je tangenta paralelna oko x.

Kada je x ∈ - ∞ ; - 2 , zatim - 1 5 (x 2 + 12 x + 35) = 0 , a za x ∈ (- 2 ; + ∞) dobivamo 1 5 (x 2 - 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Izračunavamo odgovarajuće vrijednosti funkcije

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Dakle - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 smatraju se željenim točkama grafa funkcije.

Razmotrimo grafički prikaz rješenja.

Crna linija je graf funkcije, crvene točke su dodirne točke.

1. Kada su linije paralelne, nagibi su jednaki. Zatim je potrebno tražiti točke grafa funkcije, gdje će nagib biti jednak vrijednosti 8 5 . Da biste to učinili, morate riješiti jednadžbu oblika y "(x) = 8 5. Zatim, ako je x ∈ - ∞; - 2, dobivamo da je - 1 5 (x 2 + 12 x + 35) = 8 5, a ako je x ∈ ( - 2 ; + ∞) , tada je 1 5 (x 2 - 4 x + 3) = 8 5 .

Prva jednadžba nema korijen jer je diskriminant manji od nule. Zapišimo to

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Druga jednadžba, dakle, ima dva realna korijena

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Prijeđimo na traženje vrijednosti funkcije. Shvaćamo to

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Bodovi s vrijednostima - 1; 4 15, 5; 8 3 su točke u kojima su tangente paralelne s pravcem y = 8 5 x + 4 .

Odgovor: crna linija - graf funkcije, crvena linija - graf y \u003d 8 5 x + 4, plava linija - tangente u točkama - 1; 4 15, 5; 8 3 .

Moguće je postojanje beskonačnog broja tangenata za zadane funkcije.

Primjer 5

Napišite jednadžbe svih dostupnih tangenta funkcije y = 3 cos 3 2 x - π 4 - 1 3 , koje su okomite na pravac y = - 2 x + 1 2 .

Odluka

Za izradu jednadžbe tangente potrebno je pronaći koeficijent i koordinate dodirne točke, na temelju uvjeta okomitosti pravaca. Definicija zvuči ovako: umnožak nagiba koji su okomiti na ravne je jednak - 1, odnosno zapisuje se kao k x · k ⊥ = - 1. Iz uvjeta imamo da je nagib okomit na pravu i jednak k ⊥ = - 2, tada je k x = - 1 k ⊥ = - 1 - 2 = 1 2 .

Sada moramo pronaći koordinate dodirnih točaka. Trebate pronaći x, nakon čega je njegova vrijednost za danu funkciju. Imajte na umu da iz geometrijskog značenja derivacije u točki
x 0 dobivamo da je k x \u003d y "(x 0) . Iz ove jednakosti nalazimo x vrijednosti za dodirne točke.

Shvaćamo to

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ k x \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ sin 3 π 2 x 0 - 4 = - 1 9

Ovo je trigonometrijska jednadžba koristit će se za izračunavanje ordinata dodirnih točaka.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk ili 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk ili 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk ili x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z je skup cijelih brojeva.

Pronađeno x dodirnih točaka. Sada morate ići na traženje y vrijednosti:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 ili y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 ili y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 ili y 0 = - 4 5 + 1 3

Odavde dobivamo da je 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 su dodirne točke.

Odgovor: potrebne jednadžbe bit će zapisane kao

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Za vizualni prikaz, razmotrite funkciju i tangentu na koordinatnoj liniji.

Slika pokazuje da je mjesto funkcije na intervalu [-10; 10 ] , gdje je crna linija graf funkcije, plave linije su tangente koje su okomite na zadanu liniju oblika y = - 2 x + 1 2 . Crvene točke su dodirne točke.

Kanonske jednadžbe krivulja 2. reda nisu jednovrijedne funkcije. Tangentne jednadžbe za njih se sastavljaju prema dobro poznatim shemama.

Tangenta na kružnicu

Postaviti kružnicu sa središtem u točki x c e n t e r ; y c e n t e r i polumjer R, koristi se formula x - x c e n t e r 2 + y - y c e n t e r 2 = R 2.

Ova se jednakost može zapisati kao unija dviju funkcija:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Prva funkcija je na vrhu, a druga na dnu, kao što je prikazano na slici.

Sastaviti jednadžbu kružnice u točki x 0 ; y 0 , koji se nalazi u gornjem ili donjem polukrugu, trebali biste pronaći jednadžbu grafa funkcije oblika y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r ili y \u003d - R e 2 - x - x 2 + e y c e n t e r na navedenoj točki.

Kada je u točkama x c e n t e r ; y c e n t e r + R i x c e n t e r ; y c e n t e r - R tangente mogu se dati jednadžbama y = y c e n t e r + R i y = y c e n t e r - R , a u točkama x c e n t e r + R ; y c e n t e r i
x c e n t e r - R ; y c e n t e r će biti paralelan oko y, tada ćemo dobiti jednadžbe oblika x = x c e n t e r + R i x = x c e n t e r - R .

Tangenta na elipsu

Kad je elipsa u središtu na x c e n t e r; y c e n t e r s poluosama a i b , tada se može dati pomoću jednadžbe x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .

Elipsa i krug mogu se označiti kombiniranjem dviju funkcija, odnosno gornje i donje poluelipse. Onda to dobivamo

y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

Ako se tangente nalaze na vrhovima elipse, tada su paralelne oko x ili oko y. Radi jasnoće, razmotrite donju sliku.

Primjer 6

Napišite jednadžbu tangente na elipsu x - 3 2 4 + y - 5 2 25 = 1 u točkama s x vrijednostima jednakim x = 2 .

Odluka

Potrebno je pronaći dodirne točke koje odgovaraju vrijednosti x = 2. Napravimo zamjenu u postojećoj jednadžbi elipse i dobijemo je

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Zatim 2; 5 3 2 + 5 i 2 ; - 5 3 2 + 5 su tangente koje pripadaju gornjoj i donjoj poluelipsi.

Prijeđimo na pronalaženje i rješavanje jednadžbe elipse s obzirom na y. Shvaćamo to

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Očito je da je gornja poluelipsa specificirana pomoću funkcije oblika y = 5 + 5 2 4 - x - 3 2 , a donja y = 5 - 5 2 4 - x - 3 2 .

Primjenjujemo standardni algoritam kako bismo formulirali jednadžbu tangente na graf funkcije u točki. Zapisujemo da je jednadžba za prvu tangentu u točki 2; 5 3 2 + 5 će izgledati

y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Dobivamo da je jednadžba druge tangente s vrijednošću u točki
2; - 5 3 2 + 5 postaje

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafički se tangente označavaju na sljedeći način:

Tangenta na hiperbolu

Kada hiperbola ima središte u točki x c e n t e r; y c e n t e r i vrhovi x c e n t e r + α ; y c e n t e r i x c e n t e r - α ; y c e n t e r , dana je nejednakost x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 ako je s vrhovima x c e n t e r ; y c e n t e r + b i x c e n t e r ; y c e n t e r - b tada je dan nejednakošću x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbola se može predstaviti kao dvije kombinirane funkcije oblika

y = b a (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 - a 2 + y c e n t e r ili y = b a (x - x c t e r - c e 2 + e 2 + ) 2 + a 2 + y c e n t e r

U prvom slučaju imamo da su tangente paralelne s y, au drugom paralelne s x.

Iz toga slijedi da je za pronalaženje jednadžbe tangente na hiperbolu potrebno saznati kojoj funkciji pripada točka tangente. Da bi se to utvrdilo, potrebno je izvršiti zamjenu u jednadžbama i provjeriti njihovu identičnost.

Primjer 7

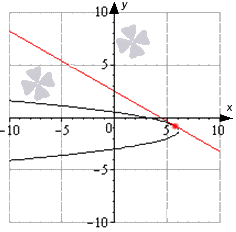
Napišite jednadžbu tangente na hiperbolu x - 3 2 4 - y + 3 2 9 = 1 u točki 7; - 3 3 - 3 .

Odluka

Potrebno je transformirati zapis rješenja nalaženja hiperbole pomoću 2 funkcije. Shvaćamo to

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 ili y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Potrebno je saznati kojoj funkciji pripada data točka s koordinatama 7; - 3 3 - 3 .

Očito, da biste provjerili prvu funkciju, trebate y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , tada točka ne pripada grafu, budući da jednakost nije zadovoljena.

Za drugu funkciju imamo da je y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , što znači da točka pripada zadanom grafu. Odavde biste trebali pronaći koeficijent nagiba.

Shvaćamo to

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Odgovor: tangentna jednadžba se može predstaviti kao

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Vizualizira se na sljedeći način:

Tangenta na parabolu

Da biste sastavili jednadžbu tangente na parabolu y \u003d a x 2 + b x + c u točki x 0, y (x 0) , morate koristiti standardni algoritam, tada će jednadžba poprimiti oblik y \u003d y " (x 0) x - x 0 + y ( x 0) Takva tangenta na vrhu je paralelna s x.

Parabolu x = a y 2 + b y + c treba definirati kao uniju dviju funkcija. Stoga moramo riješiti jednadžbu za y. Shvaćamo to

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Grafičkijmo to kao:

Da biste saznali pripada li točka x 0 , y (x 0) funkciji, nježno slijedite standardni algoritam. Takva tangenta bit će paralelna s y s obzirom na parabolu.

Primjer 8

Napišite jednadžbu tangente na graf x - 2 y 2 - 5 y + 3 kada imamo nagib tangente od 150°.

Odluka

Rješenje započinjemo predstavljanjem parabole kao dvije funkcije. Shvaćamo to

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Vrijednost nagiba jednaka je vrijednosti derivacije u točki x 0 ove funkcije i jednaka je tangenti nagiba.

dobivamo:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

Odavde određujemo vrijednost x za dodirne točke.

Prva funkcija bit će napisana kao

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Očito, nema pravih korijena, jer smo dobili negativnu vrijednost. Zaključujemo da za takvu funkciju ne postoji tangenta s kutom od 150°.

Druga funkcija će biti zapisana kao

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Imamo da dodirne točke - 23 4 ; - 5 + 3 4 .

Odgovor: tangentna jednadžba poprima oblik

y = - 1 3 x - 23 4 + - 5 + 3 4

Grafičkijmo to ovako:

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Ovaj matematički program pronalazi jednadžbu tangente na graf funkcije \(f(x) \) u točki koju je odredio korisnik \(a \).

Program ne samo da prikazuje tangentnu jednadžbu, već prikazuje i proces rješavanja problema.

Ovaj online kalkulator može biti koristan srednjoškolcima općeobrazovne škole u pripremi za kontrolni rad i ispite, prilikom provjere znanja prije ispita, roditelji kontroliraju rješavanje mnogih zadataka iz matematike i algebre. Ili vam je možda preskupo angažirati učitelja ili kupiti nove udžbenike? Ili jednostavno želite to učiniti što je prije moguće? domaća zadaća matematika ili algebra? U tom slučaju možete koristiti i naše programe s detaljnim rješenjem.

Na taj način možete provoditi vlastitu obuku i/ili obuku svoje mlađe braće ili sestara, a povećava se razina edukacije u području zadataka koje treba rješavati.

Ako trebate pronaći derivaciju funkcije, onda za to imamo zadatak Pronađi derivaciju.

Ako niste upoznati s pravilima za uvođenje funkcija, preporučujemo da se s njima upoznate.

Unesite izraz funkcije \(f(x)\) i broj \(a\)

f(x)=
a=

Pronađite jednadžbu tangente

Utvrđeno je da neke skripte potrebne za rješavanje ovog zadatka nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.

JavaScript vam je onemogućen u pregledniku.
JavaScript mora biti omogućen da bi se rješenje pojavilo.
Ovdje su upute kako omogućiti JavaScript u svom pregledniku.

Jer Ima puno ljudi koji žele riješiti problem, vaš zahtjev je u redu.
Nakon nekoliko sekundi, rješenje će se pojaviti ispod.
Molim pričekajte sek...

Ako ti uočio grešku u rješenju, onda o tome možete pisati u Obrascu za povratne informacije.
Ne zaboravi naznačiti koji zadatak ti odlučuješ što unesite u polja.

Naše igre, zagonetke, emulatori:

Malo teorije.

Nagib ravne linije

Podsjetimo da je graf linearne funkcije \(y=kx+b\) ravna linija. Poziva se broj \(k=tg \alpha \). nagib ravne linije, a kut \(\alpha \) je kut između ove linije i osi Ox

Ako je \(k>0\), tada \(0 If \(kJednadžba tangente na graf funkcije

Ako točka M (a; f (a)) pripada grafu funkcije y \u003d f (x) i ako je u ovoj točki moguće povući tangentu na graf funkcije koja nije okomita na x-osi, onda iz geometrijskog značenja derivacije proizlazi da je nagib tangente jednak f "(a). Zatim ćemo razviti algoritam za sastavljanje jednadžbe tangente na graf bilo koje funkcije.

Neka su dana funkcija y \u003d f (x) i točka M (a; f (a)) na grafu ove funkcije; neka bude poznato da f "(a) postoji. Sastavimo jednadžbu tangente na graf dane funkcije u danoj točki. Ova jednadžba, poput jednadžbe bilo koje ravne linije koja nije paralelna s y-osi , ima oblik y \u003d kx + b, pa je zadatak pronaći vrijednosti koeficijenata k i b.

Sve je jasno s nagibom k: poznato je da je k \u003d f "(a). Za izračunavanje vrijednosti b koristimo činjenicu da željena ravna linija prolazi kroz točku M (a; f (a)) To znači da ako zamijenimo koordinate točke M u jednadžbu ravne, dobivamo točnu jednakost: \ (f (a) \u003d ka + b \), tj. \ (b \u003d f (a) ) - ka \).

Ostaje zamijeniti pronađene vrijednosti koeficijenata k i b u jednadžbu ravne:

$$ y=kx+b $$ $$ y=kx+ f(a) - ka $$ $$ y=f(a)+ k(x-a) $$ $$ y=f(a)+ f"(a )(x-a) $$

Primili smo jednadžba tangente na graf funkcije\(y = f(x) \) u točki \(x=a \).

Algoritam za pronalaženje jednadžbe tangente na graf funkcije \(y=f(x)\)
1. Označite apscisu dodirne točke slovom \ (a \)
2. Izračunajte \(f(a)\)
3. Pronađite \(f"(x) \) i izračunajte \(f"(a) \)
4. Zamijenite pronađene brojeve \ (a, f (a), f "(a) \) u formulu \ (y \u003d f (a) + f "(a) (x-a) \)

Knjige (udžbenici) Sažeci Jedinstvenog državnog ispita i OGE testova online Igre, zagonetke Grafički prikaz funkcija Pravopisni rječnik ruskog jezika Rječnik slenga mladih Katalog ruskih škola Katalog srednjih škola u Rusiji Katalog ruskih sveučilišta Popis zadataka Pronalaženje GCD i LCM Pojednostavljivanje polinoma (množenje polinoma)

Neka je dana funkcija f koja u nekoj točki x 0 ima konačan izvod f (x 0). Tada pravac koji prolazi točkom (x 0; f (x 0)), koja ima nagib f '(x 0), naziva se tangenta.

Ali što se događa ako derivacija u točki x 0 ne postoji? Postoje dvije opcije:

1. Tangenta na graf također ne postoji. Klasičan primjer je funkcija y = |x | u točki (0; 0).
2. Tangenta postaje okomita. To vrijedi, na primjer, za funkciju y = arcsin x u točki (1; π /2).

Jednadžba tangente

Svaka neokomita ravna crta dana je jednadžbom oblika y = kx + b, gdje je k nagib. Tangenta nije iznimka, a da bi se sastavila njena jednadžba u nekoj točki x 0, dovoljno je znati vrijednost funkcije i derivacije u ovoj točki.

Dakle, neka je funkcija data y = f (x), koja ima derivaciju y = f '(x) na segmentu. Tada se u bilo kojoj točki x 0 ∈ (a; b) može povući tangenta na graf ove funkcije, koja je dana jednadžbom:

y \u003d f '(x 0) (x - x 0) + f (x 0)

Ovdje je f ’(x 0) vrijednost derivacije u točki x 0, a f (x 0) je vrijednost same funkcije.

Zadatak. Zadana je funkcija y = x 3 . Napišite jednadžbu za tangentu na graf ove funkcije u točki x 0 = 2.

Jednadžba tangente: y \u003d f '(x 0) (x - x 0) + f (x 0). Točka x 0 = 2 nam je dana, ali će se morati izračunati vrijednosti f (x 0) i f '(x 0).

Prvo, pronađimo vrijednost funkcije. Ovdje je sve jednostavno: f (x 0) = f (2) = 2 3 = 8;
Sada pronađimo derivaciju: f '(x) = (x 3) ' = 3x 2;
Zamjena u izvodu x 0 = 2: f '(x 0) = f '(2) = 3 2 2 = 12;
Tako dobivamo: y = 12 (x - 2) + 8 = 12x - 24 + 8 = 12x - 16.
Ovo je jednadžba tangente.

Zadatak. Sastavite jednadžbu tangente na graf funkcije f (x) \u003d 2sin x + 5 u točki x 0 \u003d π / 2.

Ovaj put nećemo detaljno opisivati ​​svaku radnju - samo ćemo naznačiti ključne korake. Imamo:

f (x 0) \u003d f (π / 2) \u003d 2sin (π / 2) + 5 = 2 + 5 \u003d 7;
f '(x) \u003d (2sin x + 5) ' \u003d 2cos x;
f '(x 0) \u003d f '(π / 2) \u003d 2cos (π / 2) \u003d 0;

Tangentna jednadžba:

y = 0 (x − π /2) + 7 ⇒ y = 7

U potonjem slučaju, linija se pokazala vodoravnom, jer njegov nagib k = 0. U tome nema ništa loše - upravo smo naišli na točku ekstrema.

Uputa

Određujemo nagib tangente na krivulju u točki M.
Krivulja koja predstavlja graf funkcije y = f(x) je kontinuirana u nekom susjedstvu točke M (uključujući samu točku M).

Ako vrijednost f‘(x0) ne postoji, tada ili nema tangente, ili prolazi okomito. S obzirom na to, prisutnost derivacije funkcije u točki x0 posljedica je postojanja nevertikalne tangente koja je u kontaktu s grafom funkcije u točki (x0, f(x0)). U ovom slučaju, nagib tangente će biti jednak f "(x0). Dakle, geometrijsko značenje derivacije postaje jasno - izračunavanje nagiba tangente.

Pronađite vrijednost apscise dodirne točke, koja je označena slovom "a". Ako se podudara s danom tangentnom točkom, tada će "a" biti njena x-koordinata. Odredite vrijednost funkcije f(a), zamjenjujući u jednadžbu funkcije veličina apscise.

Odredite prvi izvod jednadžbe funkcije f'(x) i u nju zamijeniti vrijednost točke "a".

Uzmite opću tangentnu jednadžbu, koja je definirana kao y = f (a) = f (a) (x - a), i zamijenite pronađene vrijednosti a, f (a), f "( a) u nju. Kao rezultat, rješenje grafa će biti pronađeno i tangentno.

Zadatak riješite na drugačiji način ako se zadana tangentna točka ne poklapa s tangentnom točkom. U tom slučaju potrebno je umjesto brojeva u jednadžbi tangente zamijeniti "a". Nakon toga, umjesto slova "x" i "y", zamijenite vrijednost koordinata zadanu točku. Riješi rezultirajuću jednadžbu u kojoj je "a" nepoznanica. Dobivenu vrijednost stavite u jednadžbu tangente.

Napišite jednadžbu za tangentu sa slovom "a", ako je jednadžba data u uvjetu zadatka funkcije te jednadžba paralelnog pravca s obzirom na željenu tangentu. Nakon toga treba vam izvedenica funkcije