Formules de la théorie des probabilités et exemples d'examens. Théorie des probabilités

Événement aléatoire Tout événement qui peut ou non se produire à la suite d'une expérience.

Probabilité d'événement R est égal au rapport du nombre de résultats favorables k parmi toutes les issues possibles. n, c'est à dire.

p=\frac(k)(n)

Formules d'addition et de multiplication de la théorie des probabilités

événement \bar(A) appelé opposé à l'événement A, si l'événement A ne s'est pas produit.

Somme des probabilités événements opposés est égal à un, c'est-à-dire

P(\bar(A)) + P(A) =1

• La probabilité d'un événement ne peut pas être supérieure à 1.
• Si la probabilité d'un événement est de 0, alors il ne se produira pas.
• Si la probabilité d'un événement est de 1, alors il se produira.

Théorème d'addition de probabilité :

"La probabilité de la somme de deux événements incompatibles est égale à la somme des probabilités de ces événements."

P(A+B) = P(A) + P(B)

Probabilité les montants deux événements communs est égal à la somme des probabilités de ces événements sans tenir compte de leur occurrence conjointe :

P(A+B) = P(A) + P(B) - P(AB)

Théorème de multiplication de probabilité

"La probabilité du produit de deux événements est égale au produit des probabilités de l'un d'eux par la probabilité conditionnelle de l'autre, calculée sous la condition que le premier ait eu lieu."

P(AB)=P(A)*P(B)

Développements appelé incompatible, si l'apparition de l'un d'eux exclut l'apparition des autres. C'est-à-dire qu'un seul événement particulier peut se produire, ou un autre.

Développements appelé découper, à moins que la survenance de l'un d'eux n'empêche la survenance de l'autre.

Deux événements aléatoires A et B sont appelés indépendant, si l'occurrence de l'un d'eux ne change pas la probabilité d'occurrence de l'autre. Sinon, les événements A et B sont dits dépendants.

Probabilité. Tâches de l'examen de profil en mathématiques.

Préparé par un professeur de mathématiques au MBOU "Lyceum No. 4", Ruzaevka

Ovchinnikova T.V.

Définition de la probabilité

Probabilité événements A appeler le rapport du nombre m résultats favorables à cet événement au nombre total n tous les événements incompatibles également possibles qui peuvent survenir à la suite d'un seul test ou d'une seule observation :

m

n

Laisser k - le nombre de lancers de pièces, puis le nombre de résultats possibles : n=2 k .

Laisser k - le nombre de lancers de dés, puis le nombre de résultats possibles : n=6 k .

Dans une expérience aléatoire, une pièce de monnaie symétrique est lancée deux fois. Trouvez la probabilité que face tombe exactement une fois.

La solution.

Seulement 4 options : sur; oh oh ; p p; p p; sur .

Favorable 2 : sur; R et R; sur .

La probabilité est 2/4 = 1/2 = 0,5 .

Réponse : 0,5.

Dans une expérience aléatoire, deux dés sont lancés. Trouvez la probabilité d'obtenir 8 points au total. Arrondis le résultat au centième près.

La solution.

Les dés sont des dés à 6 faces. Le premier dé peut obtenir 1, 2, 3, 4, 5 ou 6 points. Chaque option de score correspond à 6 options de score sur le second dé.

Ceux. Total diverses options 6x6=36.

Les options (résultats de l'expérience) seront les suivantes :

1; 1 1; 2 1; 3 1; 4 1; 5 1; 6

2; 1 2; 2 2; 3 2; 4 2; 5 2; 6

etc. ...............................................

6; 1 6; 2 6; 3 6; 4 6; 5 6; 6

Comptons le nombre de résultats (options) dans lesquels la somme des points de deux dés est 8.

2; 6 3; 5; 4; 4 5; 3 6; 2.

Seulement 5 options.

Trouvons la probabilité : 5/36 = 0,138 ≈ 0,14.

Réponse : 0,14.

Il y a au total 55 tickets dans la collection de tickets de biologie, 11 d'entre eux contiennent une question sur la botanique. Trouvez la probabilité qu'un étudiant reçoive une question sur la botanique dans un ticket d'examen sélectionné au hasard.

La solution:

La probabilité qu'un étudiant reçoive une question sur la botanique dans un ticket d'examen sélectionné au hasard est de 11/55 = 1/5 = 0,2.

Réponse : 0,2.

20 athlètes participent au championnat de gymnastique : 8 de Russie, 7 des États-Unis, le reste de Chine. L'ordre de passage des gymnastes est déterminé par tirage au sort. Trouvez la probabilité que l'athlète qui concourt en premier soit originaire de Chine.

La solution.

Il y a 20 athlètes au total.

dont 20 - 8 - 7 = 5 athlètes chinois.

La probabilité que l'athlète qui concourt en premier soit originaire de Chine est de 5/20 = 1/4 = 0,25.

Réponse : 0,25.

La conférence scientifique se tient dans 5 jours. Au total, 75 rapports sont prévus - les trois premiers jours, 17 rapports chacun, les autres sont répartis également entre les quatrième et cinquième jours. L'ordre des rapports est déterminé par un tirage au sort. Quelle est la probabilité que le rapport du professeur M. soit programmé pour le dernier jour de la conférence ?

La solution:

Le dernier jour de la conférence est prévu

(75 - 17 × 3) : 2 = 12 rapports.

La probabilité que le rapport du professeur M. soit programmé pour le dernier jour de la conférence est de 12/75 = 4/25 = 0,16.

Réponse : 0,16.

Avant le début du premier tour du championnat de badminton, les participants sont répartis au hasard en paires de jeu par tirage au sort. Au total, 26 joueurs de badminton participent au championnat, dont 10 participants de Russie, dont Ruslan Orlov. Trouvez la probabilité qu'au premier tour, Ruslan Orlov joue avec n'importe quel joueur de badminton de Russie ?

La solution:

Il convient de noter que Ruslan Orlov doit jouer avec un joueur de badminton russe. Et Ruslan Orlov lui-même est également originaire de Russie.

La probabilité qu'au premier tour Ruslan Orlov joue avec n'importe quel joueur de badminton russe est de 9/25 = 36/100 = 0,36.

Réponse : 0,36.

Dasha lance les dés deux fois. Elle a marqué 8 points au total. Trouvez la probabilité d'obtenir 2 au premier lancer.

La solution.

Au total, les deux dés devraient rapporter 8 points. Ceci est possible s'il existe les combinaisons suivantes :

Seulement 5 options. Comptons le nombre de résultats (options) dans lesquels 2 points sont tombés au premier lancer.

Cette option est 1.

Trouvez la probabilité : 1/5 = 0,2.

Réponse : 0,2.

Il y a 20 équipes participant au championnat du monde. Avec l'aide de lots, ils doivent être divisés en cinq groupes de quatre équipes chacun. Dans la boîte se trouvent des cartes mixtes avec des numéros de groupe :

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.

Les capitaines d'équipe piochent chacun une carte. Quelle est la probabilité que l'équipe russe soit dans le troisième groupe.

La solution:

Il y a 20 équipes au total, 5 groupes.

Chaque groupe comporte 4 équipes.

Donc, au total, nous avons obtenu 20 résultats, nous en avions besoin de 4, ce qui signifie que la probabilité que le résultat souhaité tombe est de 4/20 = 0,2.

Réponse : 0,2.

Deux usines produisent le même verre pour les phares des voitures. La première usine produit 45% de ces verres, la seconde - 55%. La première usine produit 3% de verres défectueux et la seconde - 1%. Trouvez la probabilité qu'un verre acheté accidentellement dans un magasin soit défectueux.

La solution:

La probabilité que le verre ait été acheté à la première usine et qu'il soit défectueux :

R 1 = 0,45 0,03 = 0,0135.

La probabilité que le verre ait été acheté à la deuxième usine et qu'il soit défectueux :

R 2 = 0,55 0,01 = 0,0055.

Par conséquent, selon la formule de probabilité totale, la probabilité qu'un verre acheté accidentellement dans un magasin soit défectueux est

p = p 1 +p 2 = 0,0135 + 0,0055 = 0,019.

Réponse : 0,019.

Si le grand maître A. joue blanc, alors il gagne le grand maître B. avec une probabilité de 0,52. Si A. joue noir, alors A. bat B. avec une probabilité de 0,3.

Les grands maîtres A. et B. jouent deux jeux, et dans le deuxième jeu, ils changent la couleur des pièces. Trouvez la probabilité que A. gagne les deux fois.

La solution:

Les chances de gagner les premier et deuxième jeux sont indépendantes l'une de l'autre. La probabilité de produire des événements indépendants est égale au produit de leurs probabilités :

p = 0,52 0,3 = 0,156.

Réponse : 0,156.

Le biathlète tire cinq fois sur les cibles. La probabilité d'atteindre la cible d'un seul coup est de 0,8. Trouvez la probabilité que le biathlète atteigne les cibles les trois premières fois et rate les deux dernières. Arrondis le résultat au centième près.

La solution:

Le résultat de chaque tir suivant ne dépend pas des précédents. Par conséquent, les événements « touché au premier coup », « touché au deuxième coup », etc. indépendant.

La probabilité de chaque succès est de 0,8. La probabilité d'un échec est donc de 1 - 0,8 = 0,2.

1 coup : 0,8

2 coups : 0,8

3 coups : 0,8

4 coups : 0,2

5 coups : 0,2

D'après la formule de multiplication des probabilités d'événements indépendants, on trouve que la probabilité recherchée est égale à :

0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.

Réponse : 0,02.

Le magasin dispose de deux machines de paiement. Chacun d'eux peut être défectueux avec une probabilité de 0,05, quel que soit l'autre automate. Trouver la probabilité qu'au moins un automate soit utilisable.

La solution:

Trouvez la probabilité que les deux automates soient défectueux.

Ces événements sont indépendants, la probabilité de leur produit est égale au produit des probabilités de ces événements :

0,05 0,05 = 0,0025.

Un événement consistant dans le fait qu'au moins un automate est utilisable est l'inverse.

Par conséquent, sa probabilité est

1 − 0,0025 = 0,9975.

Réponse : 0,9975.

Cowboy John frappe une mouche sur le mur avec une probabilité de 0,9 s'il tire avec un revolver à tir. Si John tire un revolver non tiré, il touche une mouche avec une probabilité de 0,2. Il y a 10 revolvers sur la table, dont seulement 4 sont tirés. Cowboy John voit une mouche sur le mur, attrape au hasard le premier revolver qu'il rencontre et tire sur la mouche. Trouvez la probabilité que John manque.

La solution:

La probabilité que John rate s'il attrape un coup de revolver est :

0,4 (1 - 0,9) = 0,04

La probabilité que John rate s'il attrape un revolver non tiré est :

0,6 (1 - 0,2) = 0,48

Ces événements sont incompatibles, la probabilité de leur somme est égale à la somme des probabilités de ces événements :

0,04 + 0,48 = 0,52.

Réponse : 0,52.

Lors d'un tir d'artillerie système automatique tire sur la cible. Si la cible n'est pas détruite, le système se déclenche à nouveau. Les tirs sont répétés jusqu'à ce que la cible soit détruite. La probabilité de détruire une certaine cible avec le premier tir est de 0,4, et avec chaque tir suivant, elle est de 0,6. Combien de tirs seront nécessaires pour s'assurer que la probabilité de détruire la cible est d'au moins 0,98 ?

La solution:

Vous pouvez résoudre le problème "par des actions", en calculant la probabilité de survivre après une série d'échecs successifs :

P(1) = 0,6 ;

P(2) = P(1) 0,4 = 0,24 ;

P(3) = P(2) 0,4 = 0,096 ;

P(4) = P(3) 0,4 = 0,0384 ;

P(5) = P(4) 0,4 = 0,01536.

La dernière probabilité est inférieure à 0,02, donc cinq tirs sur la cible sont suffisants.

Réponse : 5.

Il y a 26 personnes dans la classe, dont deux jumeaux - Andrey et Sergey. La classe est divisée au hasard en deux groupes de 13 personnes chacun. Trouvez la probabilité qu'Andrey et Sergey soient dans le même groupe.

La solution:

Que l'un des jumeaux soit dans un groupe.

Avec lui, 12 personnes sur les 25 camarades restants feront partie du groupe.

La probabilité que le deuxième jumeau soit parmi ces 12 personnes est égale à

P=12:25=0,48.

Réponse : 0,48.

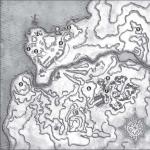
La photo montre un labyrinthe. L'araignée rampe dans le labyrinthe au point "Entrée". L'araignée ne peut pas faire demi-tour et ramper en arrière, donc, à chaque bifurcation, l'araignée choisit l'un des chemins qu'elle n'a pas encore rampé. En supposant que le choix du chemin ultérieur est purement aléatoire, déterminez avec quelle probabilité l'araignée viendra à la sortie D.

La solution:

A chacune des quatre fourches marquées, l'araignée peut choisir soit le chemin menant à la sortie D, soit un autre chemin avec une probabilité de 0,5. Ce sont des événements indépendants, la probabilité de leur produit (l'araignée atteint la sortie D) est égale au produit des probabilités de ces événements. Par conséquent, la probabilité d'arriver à la sortie D est (0,5) 4 = 0,0625.

Les événements qui se produisent dans la réalité ou dans notre imagination peuvent être divisés en 3 groupes. Ce sont certains événements qui doivent se produire, des événements impossibles et des événements aléatoires. La théorie des probabilités étudie les événements aléatoires, c'est-à-dire événements qui peuvent ou non se produire. Cet article sera présenté dans sommaire des formules de théorie des probabilités et des exemples de résolution de problèmes en théorie des probabilités, qui seront dans la tâche 4 de l'USE en mathématiques (niveau profil).

Pourquoi avons-nous besoin de la théorie des probabilités

Historiquement, la nécessité d'étudier ces problèmes est apparue au XVIIe siècle en lien avec le développement et la professionnalisation des jeux d'argent et l'avènement du casino. C'était un phénomène réel qui nécessitait son étude et ses recherches.

Jouer aux cartes, aux dés, à la roulette créait des situations où n'importe lequel d'un nombre fini d'événements également probables pouvait se produire. Il était nécessaire de donner des estimations numériques de la possibilité de survenance d'un événement.

Au XXe siècle, il est devenu clair que cette science apparemment frivole joue un rôle important dans la compréhension des processus fondamentaux se produisant dans le microcosme. A été créé théorie moderne probabilités.

Concepts de base de la théorie des probabilités

L'objet d'étude de la théorie des probabilités est les événements et leurs probabilités. Si l'événement est complexe, alors il peut être décomposé en éléments simples, dont les probabilités sont faciles à trouver.

La somme des événements A et B est appelée événement C, qui consiste dans le fait que soit l'événement A, soit l'événement B, soit les événements A et B se sont produits en même temps.

Le produit des événements A et B est l'événement C, qui consiste dans le fait que l'événement A et l'événement B se sont produits.

Les événements A et B sont dits incompatibles s'ils ne peuvent pas se produire en même temps.

Un événement A est dit impossible s'il ne peut pas se produire. Un tel événement est désigné par le symbole .

Un événement A est dit certain s'il va certainement se produire. Un tel événement est désigné par le symbole .

Attribuons à chaque événement A un numéro P(A). Ce nombre P(A) est appelé la probabilité de l'événement A si les conditions suivantes sont satisfaites avec une telle correspondance.

Un cas particulier important est la situation où il existe des issues élémentaires également probables, et arbitraires de ces issues des événements A. Dans ce cas, la probabilité peut être introduite par la formule . La probabilité ainsi introduite est appelée probabilité classique. On peut prouver que les propriétés 1 à 4 sont vérifiées dans ce cas.

Les problèmes de la théorie des probabilités, que l'on retrouve à l'examen de mathématiques, sont principalement liés à la probabilité classique. Ces tâches peuvent être très simples. Les problèmes de la théorie des probabilités sont particulièrement simples dans versions de démonstration. Il est facile de calculer le nombre de résultats favorables, le nombre de tous les résultats est écrit directement dans la condition.

Nous obtenons la réponse selon la formule.

Un exemple d'une tâche de l'examen en mathématiques pour déterminer la probabilité

Il y a 20 tartes sur la table - 5 avec du chou, 7 avec des pommes et 8 avec du riz. Marina veut prendre une tarte. Quelle est la probabilité qu'elle prenne le gâteau de riz ?

La solution.

Il y a 20 résultats élémentaires équiprobables au total, c'est-à-dire que Marina peut prendre n'importe laquelle des 20 tartes. Mais nous devons estimer la probabilité que Marina prenne la galette de riz, c'est-à-dire où A est le choix de la galette de riz. Cela signifie que nous avons un total de 8 résultats favorables (choisir des tartes au riz), puis la probabilité sera déterminée par la formule :

Événements indépendants, opposés et arbitraires

Cependant, dans la banque ouverte de tâches, plus de tâches difficiles. Attirons donc l'attention du lecteur sur d'autres questions étudiées en théorie des probabilités.

Les événements A et B sont dits indépendants si la probabilité de chacun d'eux ne dépend pas de la survenance ou non de l'autre événement.

L'événement B consiste dans le fait que l'événement A ne s'est pas produit, c'est-à-dire l'événement B est opposé à l'événement A. La probabilité de l'événement opposé est égale à un moins la probabilité de l'événement direct, c'est-à-dire .

Théorèmes d'addition et de multiplication, formules

Pour des événements arbitraires A et B, la probabilité de la somme de ces événements est égale à la somme de leurs probabilités sans la probabilité de leur événement conjoint, c'est-à-dire .

Pour les événements indépendants A et B, la probabilité du produit de ces événements est égale au produit de leurs probabilités, c'est-à-dire dans ce cas .

Les 2 derniers énoncés sont appelés les théorèmes d'addition et de multiplication des probabilités.

Ne pas toujours compter le nombre de résultats est si simple. Dans certains cas, il est nécessaire d'utiliser des formules combinatoires. Le plus important est de compter le nombre d'événements qui remplissent certaines conditions. Parfois, ces calculs peuvent devenir des tâches indépendantes.

De combien de façons peut-on asseoir 6 élèves sur 6 sièges vides ? Le premier étudiant prendra l'une des 6 places. Chacune de ces options correspond à 5 façons de placer le deuxième élève. Pour le troisième étudiant il y a 4 places libres, pour le quatrième - 3, pour le cinquième - 2, le sixième occupera la seule place restante. Pour trouver le nombre de toutes les options, vous devez trouver le produit, qui est désigné par le symbole 6 ! et lisez "six factoriel".

Dans le cas général, la réponse à cette question est donnée par la formule du nombre de permutations de n éléments : dans notre cas, .

Considérons maintenant un autre cas avec nos étudiants. De combien de façons peut-on asseoir 2 élèves sur 6 sièges vides ? Le premier étudiant prendra l'une des 6 places. Chacune de ces options correspond à 5 façons de placer le deuxième élève. Pour trouver le nombre de toutes les options, vous devez trouver le produit.

Dans le cas général, la réponse à cette question est donnée par la formule du nombre de placements de n éléments par k éléments

Dans notre cas .

Et le dernier de cette série. Combien y a-t-il de façons de choisir 3 élèves sur 6 ? Le premier étudiant peut être choisi de 6 manières, le deuxième de 5 manières et le troisième de 4 manières. Mais parmi ces options, les trois mêmes élèves se présentent 6 fois. Pour trouver le nombre de toutes les options, vous devez calculer la valeur : . Dans le cas général, la réponse à cette question est donnée par la formule du nombre de combinaisons d'éléments par éléments :

Dans notre cas .

Exemples de résolution de problèmes de l'examen en mathématiques pour déterminer la probabilité

Tâche 1. De la collection, éd. Iachtchenko.

Il y a 30 tartes dans une assiette : 3 à la viande, 18 au chou et 9 aux cerises. Sasha choisit au hasard une tarte. Trouvez la probabilité qu'il se retrouve avec une cerise.

.

Réponse : 0,3.

Problème 2. De la collection, éd. Iachtchenko.

Dans chaque lot de 1000 ampoules, une moyenne de 20 défectueuses. Trouver la probabilité qu'une ampoule choisie au hasard dans un lot soit bonne.

Solution : Le nombre d'ampoules utilisables est de 1000-20=980. Alors la probabilité qu'une ampoule prise au hasard dans le lot soit utilisable est :

Réponse : 0,98.

La probabilité que l'élève U. résolve correctement plus de 9 problèmes lors d'un test de mathématiques est de 0,67. La probabilité que U. résolve correctement plus de 8 problèmes est de 0,73. Trouvez la probabilité que U. résolve correctement exactement 9 problèmes.

Si nous imaginons une droite numérique et marquons les points 8 et 9 dessus, alors nous verrons que la condition "U. résoudre correctement exactement 9 problèmes » est inclus dans la condition « U. résoudre correctement plus de 8 problèmes », mais ne s'applique pas à la condition « W. résoudre correctement plus de 9 problèmes.

Cependant, la condition "U. résoudre correctement plus de 9 problèmes » est contenu dans la condition « U. résoudre correctement plus de 8 problèmes. Ainsi, si nous désignons des événements : « W. résoudre correctement exactement 9 problèmes" - à A, "U. résoudre correctement plus de 8 problèmes" - à B, "U. résoudre correctement plus de 9 problèmes ”via C. Ensuite, la solution ressemblera à ceci:

Réponse : 0,06.

Dans l'examen de géométrie, l'étudiant répond à une question de la liste des questions d'examen. La probabilité qu'il s'agisse d'une question de trigonométrie est de 0,2. La probabilité qu'il s'agisse d'une question sur les coins extérieurs est de 0,15. Il n'y a pas de questions liées à ces deux sujets en même temps. Trouvez la probabilité que l'étudiant obtienne une question sur l'un de ces deux sujets à l'examen.

Réfléchissons aux événements que nous avons. On nous donne deux événements incompatibles. Autrement dit, soit la question portera sur le sujet "Trigonométrie", soit sur le sujet "Angles externes". D'après le théorème des probabilités, la probabilité d'événements incompatibles est égale à la somme des probabilités de chaque événement, il faut trouver la somme des probabilités de ces événements, soit :

Réponse : 0,35.

La salle est éclairée par une lanterne à trois lampes. La probabilité qu'une lampe brûle en un an est de 0,29. Trouvez la probabilité qu'au moins une lampe ne grille pas en un an.

Considérons les événements possibles. Nous avons trois ampoules, dont chacune peut ou non griller indépendamment de toute autre ampoule. Ce sont des événements indépendants.

Ensuite, nous indiquerons les variantes de tels événements. Nous acceptons la notation : - l'ampoule est allumée, - l'ampoule est grillée. Et immédiatement après, nous calculons la probabilité d'un événement. Par exemple, la probabilité d'un événement dans lequel trois événements indépendants « ampoule grillée », « ampoule allumée », « ampoule allumée » se sont produits : .

Planifier un atelier pour les professeurs de mathématiques de l'établissement d'enseignement de la ville de Tula sur le thème «Résoudre des tâches USE en mathématiques à partir des sections: combinatoire, théorie des probabilités. Méthodes d'enseignement"

Passer du temps: 12 00 ; 15 00

Emplacement: MBOU "Lycée n°1", salle. N° 8

JE. Résolution de problèmes pour les probabilités

1. Résoudre des problèmes sur la définition classique de la probabilité

En tant qu'enseignants, nous savons déjà que les principaux types de tâches de l'USE en théorie des probabilités sont basés sur définition classique probabilités. Rappelez-vous ce qu'on appelle la probabilité d'un événement ?

Probabilité d'un événement est le rapport du nombre de résultats qui favorisent un événement donné au nombre total de résultats.

Dans notre association scientifique et méthodologique des professeurs de mathématiques, un régime général résolution de problèmes pour les probabilités. Je voudrais le présenter à votre attention. Soit dit en passant, nous avons partagé notre expérience de travail, et dans les documents que nous avons portés à votre attention pour une discussion commune sur la résolution de problèmes, nous avons donné ce schéma. Cependant, je veux l'exprimer.

À notre avis, ce schéma permet de tout mettre rapidement et logiquement sur les étagères, et après cela, la tâche peut être résolue beaucoup plus facilement pour l'enseignant et les élèves.

Donc, je veux analyser en détail le problème du contenu suivant.

Je voulais parler avec vous afin d'expliquer la méthodologie sur la façon de transmettre une telle solution aux gars, au cours de laquelle les gars comprendraient cette tâche typique, et plus tard ils comprendraient eux-mêmes ces tâches.

Qu'est-ce qu'une expérience aléatoire dans ce problème ? Maintenant, nous devons isoler l'événement élémentaire dans cette expérience. Quel est cet événement élémentaire ? Listons-les.

Des questions?

Chers collègues, vous aussi, vous avez manifestement réfléchi aux problèmes de probabilité avec les dés. Je pense qu'il faut le démonter, car il y a quelques nuances. Analysons ce problème selon le schéma que nous vous avons proposé. Puisqu'il y a un nombre de 1 à 6 sur chaque face du cube, les événements élémentaires sont les nombres 1, 2, 3, 4, 5, 6. Nous avons trouvé que nombre totalévénements élémentaires est égal à 6. Déterminons quels événements élémentaires favorisent l'événement. Seuls deux événements favorisent cet événement - 5 et 6 (puisqu'il découle de la condition que 5 et 6 points doivent tomber).

Expliquez que tous les événements élémentaires sont également possibles. Quelles seront les questions sur la tâche ?

Comment comprendre que la pièce est symétrique ? Soyons clairs, parfois certaines phrases provoquent des malentendus. Comprenons ce problème conceptuellement. Traitons avec vous dans cette expérience, qui est décrite, quels peuvent être les résultats élémentaires. Pouvez-vous imaginer où est la tête, où est la queue ? Quelles sont les options de retombées ? Y a-t-il d'autres événements ? Quel est le nombre total d'événements ? Selon le problème, on sait que les têtes sont tombées exactement une fois. Alors cet événementévénements élémentaires de ces quatre faveurs OR et RO, cela ne peut pas déjà se produire deux fois. Nous utilisons la formule par laquelle la probabilité d'un événement est trouvée. Rappelez-vous que les réponses de la partie B doivent être soit un nombre entier soit un nombre décimal.

Afficher sur le tableau blanc interactif. Nous lisons la tâche. Quel est le résultat élémentaire de cette expérience ? Précisez que la paire est ordonnée - c'est-à-dire que le nombre est tombé sur le premier dé et sur le deuxième dé. Dans toute tâche, il y a des moments où il faut choisir des méthodes rationnelles, des formulaires et présenter la solution sous forme de tableaux, schémas, etc. Dans ce problème, il est commode d'utiliser une telle table. je te donne déjà clé en main, mais au cours de la résolution, il s'avère que dans ce problème, il est rationnel d'utiliser la solution sous la forme d'un tableau. Expliquez ce que signifie le tableau. Vous comprenez pourquoi les colonnes indiquent 1, 2, 3, 4, 5, 6.

Dessinons un carré. Les lignes correspondent aux résultats du premier lancer - il y en a six, car le dé a six faces. Tout comme les colonnes. Dans chaque cellule, nous écrivons la somme des points perdus. Montrez le tableau rempli. Colorons les cellules où la somme est égale à huit (comme requis dans la condition).

Je crois que le problème suivant, après avoir analysé les précédents, peut être confié aux gars pour qu'ils le résolvent eux-mêmes.

Dans les problèmes suivants, il n'est pas nécessaire d'écrire tous les résultats élémentaires. Il suffit juste de compter leur nombre.

(Sans solution) J'ai donné aux gars de résoudre ce problème par eux-mêmes. Algorithme de résolution du problème

1. Déterminez ce qu'est une expérience aléatoire et ce qu'est un événement aléatoire.

2. Trouvez le nombre total d'événements élémentaires.

3. Nous trouvons le nombre d'événements qui favorisent l'événement spécifié dans la condition du problème.

4. Trouvez la probabilité d'un événement en utilisant la formule.

On peut poser une question aux étudiants, si 1000 batteries sont mises en vente, et parmi elles 6 sont défectueuses, alors la batterie sélectionnée est déterminée comme ? Qu'en est-il de notre tâche ? Ensuite, je pose une question sur la recherche de ce qui est utilisé ici comme nombreet je propose de le trouverNuméro. Alors je demande, quel est l'événement ici? Combien d'accumulateurs favorisent la réalisation de l'événement ? Ensuite, en utilisant la formule, nous calculons cette probabilité.

Ici, les enfants peuvent se voir proposer une seconde solution. Discutons de ce que cette méthode peut être?

1. Quel événement peut être considéré maintenant ?

2. Comment trouver la probabilité d'un événement donné ?

Il faut parler aux enfants de ces formules. Ils sont à côté

La huitième tâche peut être proposée aux enfants seuls, puisqu'elle est similaire à la sixième tâche. Il peut leur être proposé comme travail indépendant, ou sur une carte au tableau.

Ce problème peut être résolu par rapport à l'Olympiade, qui se déroule actuellement. Malgré le fait que différents événements participent aux tâches, cependant, les tâches sont typiques.

2. Les règles et formules les plus simples pour calculer les probabilités (événements opposés, somme d'événements, produit d'événements)

C'est une tâche de UTILISER la collection. Nous mettons la solution au tableau. Quelles questions devrions-nous poser aux élèves pour analyser ce problème.

1. Combien y avait-il de mitrailleuses ? Une fois deux automates, il y a déjà deux événements. Je demande aux enfants quel sera l'événement? Quel sera le deuxième événement ?

2. est la probabilité de l'événement. Nous n'avons pas besoin de le calculer, puisqu'il est donné dans la condition. Selon l'état du problème, la probabilité qu'"il n'y ait plus de café dans les deux machines" est de 0,12. Il y a eu un événement A, il y a eu un événement B. Et un nouvel événement apparaît ? Je pose aux enfants la question - quoi? Il s'agit d'un événement lorsque les deux distributeurs automatiques sont à court de café. Dans ce cas, dans la théorie des probabilités, il s'agit d'un nouvel événement, qui est appelé l'intersection de deux événements A et B et est noté de cette manière.

Utilisons la formule d'addition de probabilité. La formule est la suivante

Nous vous le donnons dans le matériel de référence et les gars peuvent donner cette formule. Il vous permet de trouver la probabilité de la somme des événements. On nous a demandé la probabilité de l'événement opposé, dont la probabilité est trouvée par la formule.

Le problème 13 utilise le concept d'un produit d'événements, dont la formule pour trouver la probabilité est donnée en annexe.

3. Tâches pour l'utilisation de l'arbre choix

Selon l'état du problème, il est facile d'établir un schéma et de trouver les probabilités indiquées.

Avec quelle aide matériel théorique Avez-vous travaillé avec des étudiants pour résoudre des problèmes de ce genre? Avez-vous utilisé un arbre des possibilités ou avez-vous utilisé d'autres méthodes pour résoudre ces problèmes ? Avez-vous donné le concept de graphes? En cinquième ou sixième année, les gars ont de tels problèmes, dont l'analyse donne le concept de graphiques.

J'aimerais vous demander si vous et vos élèves avez envisagé d'utiliser un arbre des possibilités pour résoudre des problèmes de probabilité ? Le fait est que non seulement l'USE a de telles tâches, mais des tâches plutôt complexes sont apparues, que nous allons maintenant résoudre.

Discutons avec vous de la méthodologie pour résoudre de tels problèmes - si cela coïncide avec ma méthodologie, comme je l'explique aux gars, il me sera alors plus facile de travailler avec vous, sinon, je vous aiderai à résoudre ce problème.

Discutons des événements. Quels événements du problème 17 peuvent être identifiés ?

Lors de la construction d'un arbre sur un plan, un point est désigné, appelé racine de l'arbre. Ensuite, nous commençons à considérer les événementset. Nous allons construire un segment (en théorie des probabilités, on l'appelle une branche). La condition dit que la première usine produit 30% téléphones portables cette marque (quoi? Celle qu'ils produisent), donc dans ce moment Je demande aux étudiants, quelle est la probabilité que la première usine produise des téléphones de cette marque, ceux qu'ils produisent ? Étant donné que l'événement est la sortie du téléphone à la première usine, la probabilité de cet événement est de 30 % ou 0,3. Les téléphones restants sont produits dans la deuxième usine - nous construisons le deuxième segment et la probabilité de cet événement est de 0,7.

On pose aux étudiants la question - quel type de téléphone peut être produit par la première usine ? Avec ou sans défaut. Quelle est la probabilité que le téléphone produit par la première usine présente un défaut ? Selon la condition, on dit qu'il est égal à 0,01. Question : Quelle est la probabilité que le téléphone produit par la première usine ne présente pas de défaut ? Puisque cet événement est opposé à celui donné, sa probabilité est égale.

Il est nécessaire de trouver la probabilité que le téléphone soit défectueux. Cela peut provenir de la première usine ou de la seconde. Ensuite, nous utilisons la formule d'addition des probabilités et nous obtenons que la probabilité entière est la somme des probabilités que le téléphone soit défectueux de la première usine et que le téléphone soit défectueux de la deuxième usine. La probabilité que le téléphone ait un défaut et ait été produit dans la première usine est trouvée par la formule du produit des probabilités, qui est donnée en annexe.

4. L'un des plus tâches difficiles de la banque USE pour la probabilité

Analysons, par exemple, le n° 320199 du FIPI Task Bank. C'est l'une des tâches les plus difficiles en B6.

Pour entrer à l'institut de spécialité "Linguistique", le candidat Z. doit obtenir au moins 70 points à l'examen d'État unifié dans chacune des trois matières - mathématiques, langue russe et langue étrangère. Pour entrer dans la spécialité "Commerce", vous devez obtenir au moins 70 points dans chacune des trois matières - mathématiques, langue russe et études sociales.

La probabilité que le candidat Z. reçoive au moins 70 points en mathématiques est de 0,6, en russe - 0,8, en une langue étrangère- 0,7 et en études sociales - 0,5.

Trouver la probabilité que Z. puisse entrer dans au moins une des deux spécialités citées.

Notez que le problème ne demande pas si un candidat nommé Z. étudiera à la fois la linguistique et le commerce et recevra deux diplômes. Ici, nous devons trouver la probabilité que Z. puisse entrer dans au moins une de ces deux spécialités - c'est-à-dire qu'il gagnera quantité requise points.

Pour entrer dans au moins une des deux spécialités, Z. doit obtenir au moins 70 points en mathématiques. Et en russe. Et pourtant - sciences sociales ou étrangères.

La probabilité de marquer 70 points en mathématiques pour lui est de 0,6.

La probabilité de marquer des points en mathématiques et en russe est égale.

Parlons des études étrangères et sociales. Les options nous conviennent lorsque le candidat a marqué des points en études sociales, en langue étrangère ou dans les deux. L'option ne convient pas lorsqu'il n'a pas marqué de points ni en langue ni en « société ». Cela signifie que la probabilité de réussir des études sociales ou étrangères est égale à au moins 70 points. En conséquence, la probabilité de réussir des études mathématiques, russes et sociales ou étrangères est égale à

C'est la réponse.

II . Résolution de problèmes combinatoires

1. Nombre de combinaisons et factorielles

Analysons brièvement le matériel théorique.

Expressionn ! se lit "en-factorial" et désigne le produit de tous nombres naturels de 1 àn compris:n ! = 1 2 3 ...n .

De plus, en mathématiques, par définition, on considère que 0 ! = 1. Une telle expression est rare, mais se produit toujours dans les problèmes de théorie des probabilités.

Définition

Soit des objets (crayons, bonbons, peu importe) parmi lesquels il faut choisir des objets exactement différents. Alors le nombre d'options pour un tel choix est appelénombre de combinaisons à partir des éléments. Ce nombre est indiqué et calculé selon une formule spéciale.

La désignation

Que nous donne cette formule ? En fait, presque aucune tâche sérieuse ne peut être résolue sans elle.

Pour mieux comprendre, analysons quelques problèmes combinatoires simples :

Une tâche

Le barman propose 6 variétés de thé vert. Pour la cérémonie du thé, vous devez soumettre thé vert exactement 3 différentes variétés. De combien de manières un barman peut-il terminer une commande ?

La solution

Tout est simple ici : il y an = 6 variétés au choixk = 3 variétés. Le nombre de combinaisons peut être trouvé par la formule :

Réponse

Substitut dans la formule. Nous ne pouvons pas résoudre tous les problèmes, mais tâches typiques nous avons écrit, ils sont présentés à votre attention.

Une tâche

Dans un groupe de 20 étudiants, 2 représentants doivent être sélectionnés pour prendre la parole lors de la conférence. De combien de manières cela peut-il être fait ?

La solution

Encore une fois, tout ce que nous avonsn = 20 élèves, mais il faut choisirk = 2 élèves. Trouver le nombre de combinaisons :

Veuillez noter que les facteurs inclus dans les différents factoriels sont marqués en rouge. Ces multiplicateurs peuvent être réduits sans douleur et ainsi réduire considérablement le nombre total de calculs.

Réponse

190

Une tâche

17 serveurs avec divers défauts ont été amenés à l'entrepôt, ce qui coûte 2 fois moins cher que les serveurs normaux. Le directeur a acheté 14 serveurs de ce type pour l'école et a dépensé l'argent économisé d'un montant de 200 000 roubles pour l'achat d'autres équipements. De combien de manières un directeur peut-il choisir des serveurs défectueux ?

La solution

Il y a beaucoup de données supplémentaires dans la tâche, ce qui peut prêter à confusion. Plus faits importants: il y a toutn = 17 serveurs, et le réalisateur a besoink = 14 serveurs. On compte le nombre de combinaisons :

La couleur rouge indique à nouveau les multiplicateurs qui sont réduits. Au total, il s'est avéré 680 combinaisons. En général, le réalisateur a l'embarras du choix.

Réponse

680

Cette tâche est capricieuse, car il y a des données supplémentaires dans cette tâche. Ils confondent de nombreux étudiants bonne décision. Il y avait 17 serveurs au total, et le directeur devait en choisir 14. En remplaçant dans la formule, nous obtenons 680 combinaisons.

2. Loi de multiplication

Définition

loi de multiplication en combinatoire : le nombre de combinaisons (voies, combinaisons) dans des ensembles indépendants est multiplié.

En d'autres termes, qu'il y aitUN manières d'effectuer une action etB façons d'effectuer une autre action. Le chemin aussi ces actions sont indépendantes, c'est-à-dire en aucun cas lié. Ensuite, vous pouvez trouver le nombre de façons d'effectuer la première et la deuxième action par la formule :C = UN · B .

Une tâche

Petya a 4 pièces de 1 rouble chacune et 2 pièces de 10 roubles chacune. Petya, sans regarder, a sorti de sa poche 1 pièce d'une valeur nominale de 1 rouble et une autre pièce d'une valeur nominale de 10 roubles pour acheter un stylo à 11 roubles. De combien de manières peut-il choisir ces pièces ?

La solution

Donc, Petya obtient d'abordk = 1 pièce den = 4 pièces disponibles d'une valeur nominale de 1 rouble. Le nombre de façons de le faire estC 4 1 = ... = 4.

Puis Petya fouille à nouveau dans sa poche et en sortk = 1 pièce den = 2 pièces disponibles d'une valeur nominale de 10 roubles. Ici, le nombre de combinaisons estC 2 1 = ... = 2.

Comme ces actions sont indépendantes, le nombre total d'options estC = 4 2 = 8.

Réponse

Une tâche

Il y a 8 boules blanches et 12 noires dans un panier. De combien de façons pouvez-vous obtenir 2 boules blanches et 2 boules noires de ce panier ?

La solution

Total dans le paniern = 8 boules blanches au choixk = 2 balles. Ça peut être faitC 8 2 = ... = 28 façons différentes.

De plus, le panier contientn = 12 boules noires à choisir à nouveauk = 2 balles. Le nombre de façons de le faire estC 12 2 = ... = 66.

Le choix de la boule blanche et le choix de la noire étant des événements indépendants, le nombre total de combinaisons est calculé selon la loi de multiplication :C = 28 66 = 1848. Comme vous pouvez le voir, il peut y avoir pas mal d'options.

Réponse

1848

La loi de la multiplication montre de combien de manières vous pouvez effectuer une action complexe composée de deux actions simples ou plus - à condition qu'elles soient toutes indépendantes.

3. Loi d'addition

Si la loi de la multiplication opère sur des événements « isolés » qui ne dépendent pas les uns des autres, alors dans la loi de l'addition c'est le contraire qui est vrai. Il traite d'événements mutuellement exclusifs qui ne se produisent jamais en même temps.

Par exemple, "Pierre a sorti 1 pièce de sa poche" et "Pierre n'a pas sorti une seule pièce de sa poche" sont des événements mutuellement exclusifs, puisqu'il est impossible de sortir une pièce sans en sortir aucune.

De même, les événements "Balle sélectionnée au hasard - blanche" et "Balle sélectionnée au hasard - noire" s'excluent également mutuellement.

Définition

Loi d'addition en combinatoire : si deux actions mutuellement exclusives peuvent être réaliséesUN etB façons, respectivement, ces événements peuvent être combinés. Cela va générer un nouvel événement qui peut être exécutéX = UN + B façons.

En d'autres termes, lors de la combinaison d'actions mutuellement exclusives (événements, options), le nombre de leurs combinaisons s'additionne.

On peut dire que la loi d'addition est un "OU" logique en combinatoire, lorsque l'une des options mutuellement exclusives nous convient. A l'inverse, la loi de multiplication est un "ET" logique, dans lequel on s'intéresse à l'exécution simultanée de la première et de la seconde actions.

Une tâche

Il y a 9 boules noires et 7 boules rouges dans un panier. Le garçon sort 2 balles de la même couleur. De combien de manières peut-il le faire ?

La solution

Si les balles sont de la même couleur, il y a peu d'options : les deux sont soit noires, soit rouges. Évidemment, ces options s'excluent mutuellement.

Dans le premier cas, le garçon doit choisirk = 2 boules noires den = 9 disponibles. Le nombre de façons de le faire estC 9 2 = ... = 36.

De même, dans le second cas, nous choisissonsk = 2 boules rouges den = 7 possibles. Le nombre de voies estC 7 2 = ... = 21.

Il reste à trouver le nombre total de voies. Comme les variantes avec boules noires et rouges s'excluent mutuellement, selon la loi d'addition on a :X = 36 + 21 = 57.

Réponse57

Une tâche

Le stand vend 15 roses et 18 tulipes. Un élève de 9e veut acheter 3 fleurs pour son camarade de classe, et toutes les fleurs doivent être identiques. De combien de façons peut-il faire un tel bouquet ?

La solution

Selon la condition, toutes les fleurs doivent être identiques. Ainsi, nous achèterons soit 3 roses soit 3 tulipes. De toute façon,k = 3.

Dans le cas des roses, vous devrez choisir parmin = 15 options, donc le nombre de combinaisons estC 15 3 = ... = 455. Pour les tulipesn = 18, et le nombre de combinaisons -C 18 3 = ... = 816.

Puisque les roses et les tulipes sont des options mutuellement exclusives, nous travaillons selon la loi de l'addition. Obtenir le nombre total d'optionsX = 455 + 816 = 1271. C'est la réponse.

Réponse

1271

Conditions et restrictions supplémentaires

Très souvent, dans le texte du problème, il existe des conditions supplémentaires qui imposent des restrictions importantes sur les combinaisons qui nous intéressent. Comparez deux phrases :

Il y a un ensemble de 5 stylos Couleurs différentes. De combien de manières les poignées à 3 temps peuvent-elles être sélectionnées ?

Il y a un ensemble de 5 stylos de différentes couleurs. De combien de manières peut-on choisir des poignées 3 temps si l'une d'elles doit être rouge ?

Dans le premier cas, nous avons le droit de prendre toutes les couleurs que nous aimons - il n'y a pas de restrictions supplémentaires. Dans le second cas, tout est plus compliqué, puisqu'il faut choisir une poignée rouge (on suppose qu'elle est dans le jeu d'origine).

De toute évidence, toute restriction réduit considérablement le nombre total d'options. Alors, comment trouvez-vous le nombre de combinaisons dans ce cas? Rappelez-vous juste règle suivante:

Soit un ensemble den éléments au choixk éléments. Avec l'introduction de restrictions supplémentaires sur le nombren etk diminuer du même montant.

En d'autres termes, si vous devez choisir 3 stylos sur 5, et que l'un d'eux doit être rouge, alors vous devrez choisir parmin = 5 − 1 = 4 éléments park = 3 − 1 = 2 éléments. Ainsi, au lieu deC 5 3 doit être pris en compteC 4 2 .

Voyons maintenant comment cette règle fonctionne pour exemples concrets:

Une tâche

Dans un groupe de 20 étudiants, dont 2 excellents étudiants, vous devez choisir 4 personnes pour participer à la conférence. De combien de manières ces quatre peuvent-elles être choisies si les excellents étudiants doivent se rendre à la conférence ?

La solution

Il existe donc un groupe den = 20 élèves. Mais tu n'as qu'à choisirk = 4 d'entre eux. S'il n'y avait pas de restrictions supplémentaires, le nombre d'options était égal au nombre de combinaisonsC 20 4 .

Cependant, on nous a donné condition supplémentaire: 2 honneurs doivent figurer parmi ces quatre. Ainsi, selon la règle ci-dessus, nous réduisons les nombresn etk par 2. Nous avons :

Réponse

153

Une tâche

Petya a 8 pièces dans sa poche, dont 6 pièces en roubles et 2 pièces de 10 roubles. Petya déplace trois pièces dans une autre poche. De combien de manières Petya peut-elle le faire si l'on sait que les deux pièces de 10 roubles se sont retrouvées dans une autre poche ?

La solution

il y a doncn = 8 pièces. Petya changek = 3 pièces, dont 2 de dix roubles. Il s'avère que sur 3 pièces qui seront transférées, 2 sont déjà fixées, donc les numérosn etk doit être diminué de 2. Nous avons :

Réponse

III . Résolution de problèmes combinés sur l'utilisation de formules de combinatoire et de théorie des probabilités

Une tâche

Petya avait 4 roubles et 2 roubles dans sa poche. Petya, sans regarder, a déplacé trois pièces dans une autre poche. Trouvez la probabilité que les deux pièces de deux roubles soient dans la même poche.

La solution

Supposons que les deux pièces de deux roubles se retrouvent réellement dans la même poche, alors 2 options sont possibles : soit Petya ne les a pas du tout décalées, soit il a décalé les deux en même temps.

Dans le premier cas, lorsque des pièces de deux roubles n'étaient pas transférées, des pièces de 3 roubles devraient être transférées. Puisqu'il y a 4 de ces pièces au total, le nombre de façons de le faire est égal au nombre de combinaisons de 4 par 3 :C 4 3 .

Dans le second cas, lorsque les deux pièces de deux roubles ont été transférées, une pièce de rouble supplémentaire devra être transférée. Il doit être choisi parmi 4 existants, et le nombre de façons de le faire est égal au nombre de combinaisons de 4 à 1 :C 4 1 .

Trouvons maintenant le nombre total de façons de déplacer les pièces. Puisqu'il y a 4 + 2 = 6 pièces au total, et que seulement 3 d'entre elles doivent être choisies, le nombre total d'options est égal au nombre de combinaisons de 6 à 3 :C 6 3 .

Il reste à trouver la probabilité :

Réponse

0,4

Afficher sur le tableau blanc interactif. Faites attention au fait que, selon l'état du problème, Petya, sans regarder, a déplacé trois pièces dans une poche. En répondant à cette question, nous pouvons supposer que deux pièces de deux roubles sont réellement restées dans une poche. Reportez-vous à la formule pour ajouter des probabilités. Montrez à nouveau la formule.

Une tâche

Petya avait 2 pièces de 5 roubles et 4 pièces de 10 roubles dans sa poche. Petya, sans regarder, a déplacé quelques 3 pièces dans une autre poche. Trouvez la probabilité que des pièces de cinq roubles se trouvent maintenant dans des poches différentes.

La solution

Pour que les pièces de cinq roubles se trouvent dans différentes poches, vous n'avez besoin d'en déplacer qu'une seule. Le nombre de façons de faire est égal au nombre de combinaisons de 2 par 1 :C 2 1 .

Puisque Petya a transféré 3 pièces au total, il devra transférer 2 autres pièces de 10 roubles chacune. Petya a 4 de ces pièces, donc le nombre de façons est égal au nombre de combinaisons de 4 à 2 :C 4 2 .

Reste à trouver combien d'options il y a pour décaler 3 pièces sur 6 disponibles. Ce nombre, comme dans le problème précédent, est égal au nombre de combinaisons de 6 à 3 :C 6 3 .

Trouver la probabilité :

Dans la dernière étape, nous avons multiplié le nombre de façons de choisir des pièces de deux roubles et le nombre de façons de choisir des pièces de dix roubles, puisque ces événements sont indépendants.

Réponse

0,6

Ainsi, les problèmes avec les pièces ont leur propre formule de probabilité. Il est si simple et si important qu'il peut être formulé comme un théorème.

Théorème

Laisse tomber la piècen une fois que. Alors la probabilité que face tombe exactementk les temps peuvent être trouvés en utilisant la formule:

OùC n k - nombre de combinaisons den éléments park , qui est calculé par la formule :

Ainsi, pour résoudre le problème des pièces, deux nombres sont nécessaires : le nombre de lancers et le nombre de faces. Le plus souvent, ces numéros sont donnés directement dans le texte du problème. De plus, peu importe ce qu'il faut compter exactement: les queues ou les aigles. La réponse sera la même.

A première vue, le théorème semble trop lourd. Mais cela vaut un peu de pratique - et vous ne voulez plus revenir à l'algorithme standard décrit ci-dessus.

La pièce est lancée quatre fois. Trouvez la probabilité que face sorte exactement trois fois.

La solution

Selon l'état du problème, le nombre total de lancers étaitn = 4. Nombre de têtes requis :k = 3. Remplaçantn etk dans la formule :

Avec le même succès, vous pouvez compter le nombre de queues :k = 4 − 3 = 1. La réponse sera la même.

Réponse

0,25

Une tâche [ Cahier« USE 2012 en mathématiques. Tâches B6»]

La pièce est lancée trois fois. Trouvez la probabilité qu'il n'y ait jamais pile.

La solution

Ecrire à nouveau les chiffresn etk . Comme la pièce est lancée 3 fois,n = 3. Et puisqu'il ne devrait pas y avoir de pile,k = 0. Il reste à substituer les nombresn etk dans la formule :

Permettez-moi de vous rappeler que 0 ! = 1 par définition. C'est pourquoiC 3 0 = 1.

Réponse

0,125

Une tâche [ UTILISATION d'essai en mathématiques 2012. Irkoutsk]

Dans une expérience aléatoire, une pièce de monnaie symétrique est lancée 4 fois. Trouvez la probabilité que pile tombe plus de fois que pile.

La solution

Pour qu'il y ait plus de pile que de pile, ils doivent tomber soit 3 fois (alors il y aura 1 pile) ou 4 (alors il n'y aura pas de pile du tout). Trouvons la probabilité de chacun de ces événements.

Laisserp 1 - la probabilité que face tombe 3 fois. Alorsn = 4, k = 3. Nous avons :

Trouvons maintenantp 2 - la probabilité que face tombe toutes les 4 fois. Dans ce casn = 4, k = 4. Nous avons :

Pour obtenir la réponse, il reste à additionner les probabilitésp 1 etp 2 . N'oubliez pas : vous ne pouvez ajouter des probabilités que pour des événements mutuellement exclusifs. Nous avons:

p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125

Réponse

0,3125

Afin de gagner du temps lors de la préparation avec les gars de l'examen d'État unifié et du GIA, nous avons présenté des solutions à de nombreuses autres tâches que vous pouvez choisir et résoudre avec les gars.

Matériaux du GIA, examen d'État unifié de différentes années, manuels et sites.

IV. Matériel de référence

Leçon-conférence sur le thème "théorie des probabilités"

Tâche numéro 4 de l'examen 2016.

niveau profil.

1 Groupe : affectations sur l'utilisation de la formule de probabilité classique.

• Exercice 1. La compagnie de taxi a 60 disponibles voitures; 27 d'entre eux sont noirs avec des inscriptions jaunes sur les côtés, les autres sont couleur jaune avec lettrage noir. Trouvez la probabilité qu'une voiture jaune avec des inscriptions noires arrive à un appel aléatoire.

• Tâche 2. Misha, Oleg, Nastya et Galya ont tiré au sort - qui devrait commencer le match. Trouvez la probabilité que Galya ne démarre pas la partie.

• Tâche 3. En moyenne, sur 1 000 pompes de jardin vendues, 7 fuient. Trouvez la probabilité qu'une pompe choisie au hasard ne fuie pas.

• Tâche 4. Il n'y a que 15 tickets dans la collection de tickets en chimie, dans 6 d'entre eux il y a une question sur le thème "Acides". Trouvez la probabilité qu'un élève reçoive une question sur le sujet "Acides" dans un ticket sélectionné au hasard lors de l'examen.

• Tâche 5. 45 athlètes participent au championnat de plongeon, dont 4 plongeurs espagnols et 9 plongeurs américains. L'ordre des représentations est déterminé par tirage au sort. Trouvez la probabilité que le vingt-quatrième sauteur provienne des États-Unis.

• Tâche 6. La conférence scientifique se tient sur 3 jours. Au total, 40 signalements sont prévus - 8 signalements le premier jour, les autres sont répartis équitablement entre le deuxième et le troisième jour. L'ordre des rapports est déterminé par un tirage au sort. Quelle est la probabilité que le rapport du professeur M. soit programmé pour le dernier jour de la conférence ?

• Exercice 1. Avant le début du premier tour du championnat de tennis, les participants sont répartis au hasard en paires de jeu par tirage au sort. Au total, 26 joueurs de tennis participent au championnat, dont 9 participants de Russie, dont Timofey Trubnikov. Trouvez la probabilité qu'au premier tour, Timofey Troubnikov affronte n'importe quel joueur de tennis russe.

• Tâche 2. Avant le début du premier tour du championnat de badminton, les participants sont répartis au hasard en paires de jeu par tirage au sort. Au total, 76 joueurs de badminton participent au championnat, dont 22 athlètes russes, dont Viktor Polyakov. Trouvez la probabilité qu'au premier tour Victor Polyakov joue avec n'importe quel joueur de badminton de Russie.

• Tâche 3. Il y a 16 élèves dans la classe, dont deux amis - Oleg et Mikhail. La classe est divisée au hasard en 4 groupes égaux. Trouvez la probabilité qu'Oleg et Mikhail soient dans le même groupe.

• Tâche 4. Il y a 33 élèves dans la classe, dont deux amis - Andrey et Mikhail. Les élèves sont répartis au hasard en 3 groupes égaux. Trouvez la probabilité qu'Andrey et Mikhail soient dans le même groupe.

• Exercice 1 : A l'usine de vaisselle en céramique, 20% des assiettes produites sont défectueuses. Lors du contrôle qualité des produits, 70% des plaques défectueuses sont détectées. Le reste des assiettes est à vendre. Trouver la probabilité qu'une assiette choisie au hasard au moment de l'achat ne présente aucun défaut. Arrondissez votre réponse au centième près.

• Tâche 2. A l'usine de vaisselle en céramique, 30% des assiettes produites sont défectueuses. Lors du contrôle qualité des produits, 60% des plaques défectueuses sont détectées. Le reste des assiettes est à vendre. Trouver la probabilité qu'une assiette choisie au hasard au moment de l'achat soit défectueuse. Arrondissez votre réponse au centième près.

• Tâche 3 : Deux usines produisent le même verre pour les phares des voitures. La première usine produit 30% de ces verres, la seconde - 70%. La première usine produit 3% de verres défectueux et la seconde - 4%. Trouvez la probabilité qu'un verre acheté accidentellement dans un magasin soit défectueux.

2 Groupe : trouver la probabilité de l'événement opposé.

• Exercice 1. La probabilité d'atteindre le centre de la cible à une distance de 20 m pour un tireur professionnel est de 0,85. Trouvez la probabilité de ne pas toucher le centre de la cible.

• Tâche 2. Lors de la fabrication de roulements d'un diamètre de 67 mm, la probabilité que le diamètre diffère de celui spécifié de moins de 0,01 mm est de 0,965. Trouvez la probabilité qu'un roulement aléatoire ait un diamètre inférieur à 66,99 mm ou supérieur à 67,01 mm.

3 Groupe : Trouver la probabilité d'occurrence d'au moins un des événements incompatibles. Formule d'addition de probabilité.

• Exercice 1. Trouvez la probabilité qu'un dé obtienne 5 ou 6.

• Tâche 2. Il y a 30 boules dans une urne : 10 rouges, 5 bleues et 15 blanches. Trouver la probabilité de tirer une boule colorée.

• Tâche 3. Le tireur tire sur une cible divisée en 3 zones. La probabilité de toucher la première zone est de 0,45, la seconde de 0,35. Trouvez la probabilité que le tireur touche la première ou la deuxième zone d'un seul coup.

• Tâche 4. Un bus relie quotidiennement le centre du district au village. La probabilité que lundi il y ait moins de 18 passagers dans le bus est de 0,95. La probabilité qu'il y ait moins de 12 passagers est de 0,6. Trouvez la probabilité que le nombre de passagers soit compris entre 12 et 17.

• Tâche 5. La probabilité que le nouveau Bouilloire électrique servira plus d'un an, est égal à 0,97. La probabilité qu'il dure plus de deux ans est de 0,89. Trouvez la probabilité qu'elle dure moins de deux ans mais plus d'un an.

• Tâche 6. La probabilité que l'élève U. résolve correctement plus de 9 tâches d'un test de biologie est de 0,61. La probabilité que U. résolve correctement plus de 8 problèmes est de 0,73. Trouvez la probabilité que U. résolve correctement exactement 9 problèmes.

4 Groupe: Probabilité d'occurrence simultanée d'événements indépendants. Formule de multiplication de probabilité.

• Exercice 1. La salle est éclairée par une lanterne à deux lampes. La probabilité qu'une lampe brûle en un an est de 0,3. Trouvez la probabilité qu'au moins une lampe ne grille pas en un an.

• Tâche 2. La salle est éclairée par une lanterne à trois lampes. La probabilité qu'une lampe brûle en un an est de 0,3. Trouvez la probabilité qu'au moins une lampe ne grille pas en un an.

• Tâche 3. Il y a deux vendeurs dans le magasin. Chacun d'eux est occupé avec un client avec une probabilité de 0,4. Trouvez la probabilité qu'à un moment aléatoire dans le temps les deux vendeurs soient occupés en même temps (en supposant que les clients entrent indépendamment l'un de l'autre).

• Tâche 4. Il y a trois vendeurs dans le magasin. Chacun d'eux est occupé avec un client avec une probabilité de 0,2. Trouvez la probabilité qu'à un moment aléatoire, les trois vendeurs soient occupés en même temps (en supposant que les clients entrent indépendamment les uns des autres).

• Tâche 5 : Selon les avis des clients, Mikhail Mikhailovich a apprécié la fiabilité de deux magasins en ligne. La probabilité que article désiré livré du magasin A est de 0,81. La probabilité que ce produit soit livré depuis le magasin B est de 0,93. Mikhail Mikhailovich a commandé les marchandises immédiatement dans les deux magasins. En supposant que les magasins en ligne fonctionnent indépendamment les uns des autres, trouvez la probabilité qu'aucun des magasins ne livre les marchandises.

• Tâche 6 : Si le grand maître A. joue blanc, alors il gagne le grand maître B. avec une probabilité de 0,6. Si A. joue noir, alors A. bat B. avec une probabilité de 0,4. Les grands maîtres A. et B. jouent deux jeux, et dans le deuxième jeu, ils changent la couleur des pièces. Trouvez la probabilité que A. gagne les deux fois.

5 Groupe: Tâches pour l'application des deux formules.

• Exercice 1 : Tous les patients suspects d'hépatite font un test sanguin. Si le test révèle une hépatite, le résultat du test est dit positif. Chez les patients atteints d'hépatite, l'analyse donne résultat positif avec une probabilité de 0,9. Si le patient n'a pas d'hépatite, le test peut donner un résultat faussement positif avec une probabilité de 0,02. On sait que 66 % des patients admis avec suspicion d'hépatite ont en réalité une hépatite. Trouvez la probabilité que le résultat du test d'un patient admis à la clinique avec une suspicion d'hépatite soit positif.

• Tâche 2. Cowboy John frappe une mouche sur le mur avec une probabilité de 0,9 s'il tire avec un revolver à tir. Si John tire un revolver non viseur, il touche une mouche avec une probabilité de 0,2. Il y a 10 revolvers sur la table, dont seulement 4 sont tirés. Cowboy John voit une mouche sur le mur, attrape au hasard le premier revolver qu'il rencontre et tire sur la mouche. Trouvez la probabilité que John manque.

Tâche 3 :

Dans certaines régions, les observations ont montré :

1. Si le matin de juin est clair, la probabilité de pluie ce jour-là est de 0,1. 2. Si le matin de juin est nuageux, la probabilité de pluie pendant la journée est de 0,4. 3. La probabilité qu'un matin de juin soit couvert est de 0,3.

Trouvez la probabilité qu'il ne pleuve pas un jour aléatoire en juin.

Tâche 4. Pendant le tir d'artillerie, le système automatique tire sur la cible. Si la cible n'est pas détruite, le système se déclenche à nouveau. Les tirs sont répétés jusqu'à ce que la cible soit détruite. La probabilité de détruire une certaine cible avec le premier tir est de 0,3, et avec chaque tir suivant, elle est de 0,9. Combien de tirs seront nécessaires pour s'assurer que la probabilité de détruire la cible est d'au moins 0,96 ?