Kaip išspręsti sudoku būdus. Loginiai galvosūkiai

• pamoka

1. Pagrindai

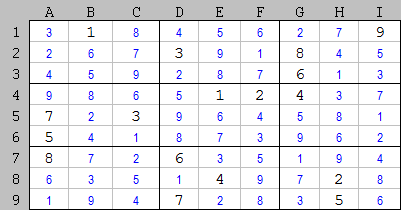
Daugelis iš mūsų, įsilaužėlių, žino, kas yra sudoku. Nekalbėsiu apie taisykles, o iškart pereisiu prie metodų.
Norint išspręsti galvosūkį, nesvarbu, koks sudėtingas ar paprastas, iš pradžių ieškoma langelių, kurias akivaizdu užpildyti.

1.1 „Paskutinis herojus“

Apsvarstykite septintąją aikštę. Tik keturios laisvos ląstelės, todėl ką nors galima greitai užpildyti.
"8 " ant D3 blokelių paminkštinimas H3 Ir J3; panašus " 8 " ant G5 užsidaro G1 Ir G2
Su ramia sąžine mes įdėjome " 8 " ant H1

1.2 „Paskutinis herojus“ iš eilės

Peržiūrėję kvadratus ir ieškodami akivaizdžių sprendimų, pereikite prie stulpelių ir eilučių.
Apsvarstykite " 4 “ Aikštėje. Aišku, kad tai bus kažkur ties linija A .
Mes turime " 4 " ant G3 kad apima A3, valgyk " 4 " ant F7, valymas A7. Ir dar vienas" 4 “ antroje aikštėje draudžia jį kartoti A4 Ir A6.
„Paskutinis herojus“ mūsų „ 4 “ tai A2

1.3 „Nėra pasirinkimo“

Kartais yra keletas priežasčių konkrečioje vietoje. "4 "į J8 būtų puikus pavyzdys.
Mėlyna rodyklės rodo, kad tai paskutinis galimas skaičius kvadratu. Raudona Ir mėlyna rodyklės nurodo paskutinį stulpelio skaičių 8 . Žalieji rodyklės nurodo paskutinį įmanomą skaičių eilutėje J.
Kaip matote, mes neturime kito pasirinkimo, kaip tik pateikti tai " 4 "vietoje.

1.4 "O kas, jei ne aš?"

Skaičius užpildyti lengviau naudojant aukščiau aprašytus metodus. Tačiau patikrinus skaičių kaip paskutinę įmanomą reikšmę, taip pat gaunami rezultatai. Metodas turėtų būti naudojamas tada, kai atrodo, kad visi skaičiai yra, bet kažko trūksta.
"5 "į B1 yra nustatytas remiantis tuo, kad visi skaičiai iš " 1 "prieš" 9 “, išskyrus „ 5 “ yra eilutėje, stulpelyje ir kvadrate (pažymėta žalia spalva).

Žargonu tai yra " nuogas vienišius". Jei užpildysite lauką su galimomis reikšmėmis​​(kandidatais), tada langelyje toks skaičius bus vienintelis galimas. Kurdami šią techniką galite ieškoti " pasislėpę vienišiai“ – unikalūs konkrečios eilutės, stulpelio ar kvadrato skaičiai.

2. „Nuoga mylia“

2.1 Nuogos poros

"„Nuoga“ pora“ – dviejų kandidatų rinkinys, esantis dviejuose langeliuose, priklausančiuose vienam bendram blokui: eilutėje, stulpelyje, kvadrate.
Aišku, kad teisingi sprendimai galvosūkiai bus tik šiose ląstelėse ir tik su šiomis reikšmėmis, o visi kiti kandidatai iš bendro bloko gali būti pašalinti.


Šiame pavyzdyje yra kelios „nuogos poros“.
raudona eilėje BET ląstelės yra paryškintos A2 Ir A3, abiejuose yra " 1 "Ir" 6 ". Dar tiksliai nežinau, kaip jie čia yra, bet visus kitus galiu drąsiai pašalinti" 1 "Ir" 6 “ iš stygos A(pažymėta geltona spalva). Taip pat A2 Ir A3 priklauso bendram kvadratui, todėl pašaliname " 1 "iš C1.

2.2 "Trys"

„Nuogos trijulės“- sudėtinga „nuogų porų“ versija.
Bet kuri trijų langelių grupė viename bloke, kurioje yra iš viso yra trys kandidatai "nuoga trijulė". Kai randama tokia grupė, šie trys kandidatai gali būti pašalinti iš kitų bloko langelių.

Kandidatų deriniai už "nuoga trijulė" gali buti taip:

// trys skaičiai trijose ląstelėse.
// bet kokie deriniai.
// bet kokie deriniai.

Šiame pavyzdyje viskas gana akivaizdu. Penktajame langelio kvadrate E4, E5, E6 yra [ 5,8,9 ], [5,8 ], [5,9 ] atitinkamai. Pasirodo, kad apskritai šios trys ląstelės turi [ 5,8,9 ], ir ten gali būti tik šie skaičiai. Tai leidžia pašalinti juos iš kitų blokavimo kandidatų. Šis triukas suteikia mums sprendimą " 3 "ląstelei E7.

2.3 „Nuostabus ketvertas“

„Nuogos keturios“ labai retas dalykas, ypač in pilna forma, ir vis tiek duoda rezultatų, kai randama. Sprendimo logika yra tokia pati kaip "nuogi trynukai".

Aukščiau pateiktame pavyzdyje pirmajame langelio kvadrate A1, B1, B2 Ir C1 paprastai yra [ 1,5,6,8 ], todėl šie skaičiai užims tik tuos langelius, o ne kitus. Geltona spalva pažymėtus kandidatus pašaliname.

3. „Viskas, kas paslėpta, tampa aišku“

3.1 Paslėptos poros

Puikus būdas atverti lauką yra paieška paslėptos poros. Šis metodas leidžia pašalinti nereikalingus kandidatus iš ląstelės ir sukurti įdomesnes strategijas.

Šiame galvosūkyje mes tai matome 6 Ir 7 yra pirmame ir antrame langeliuose. Be to 6 Ir 7 yra stulpelyje 7 . Sujungus šias sąlygas, galime teigti, kad ląstelėse A8 Ir A9 bus tik šios vertės, o mes pašalinsime visus kitus kandidatus.


Įdomesnis ir sudėtingesnis pavyzdys paslėptos poros. Pora [ 2,4 ] in D3 Ir E3, valymas 3 , 5 , 6 , 7 iš šių ląstelių. Raudonai paryškintos dvi paslėptos poros, susidedančios iš [ 3,7 ]. Viena vertus, jie yra unikalūs dviem ląstelėms 7 stulpelyje, kita vertus – eilutei E. Geltona spalva pažymėti kandidatai pašalinami.

3.1 Paslėpti trynukai

Galime vystytis paslėptos poros prieš paslėpti trynukai ar net paslėptas ketvertas. Paslėpti trys susideda iš trijų skaičių porų, esančių viename bloke. Tokie kaip ir. Tačiau, kaip ir tuo atveju "nuogi trynukai", kiekviename iš trijų langelių neturi būti trijų skaičių. dirbs Iš viso trys skaičiai trijose ląstelėse. Pavyzdžiui , , . Paslėpti trynukai bus užmaskuoti kitų kandidatų kamerose, todėl pirmiausia turite tuo įsitikinti trejetas taikomas konkrečiam blokui.


Tuo sudėtingas pavyzdys yra du paslėpti trynukai. Pirmasis, pažymėtas raudonai, stulpelyje BET. Ląstelė A4 yra [ 2,5,6 ], A7 - [2,6 ] ir langelį A9 -[2,5 ]. Šios trys ląstelės yra vienintelės, kuriose gali būti 2, 5 arba 6, todėl jos ten bus vienintelės. Todėl pašaliname nereikalingus kandidatus.

Antra, stulpelyje 9 . [4,7,8 ] yra būdingi tik ląstelėms B9, C9 Ir F9. Remdamiesi ta pačia logika, pašaliname kandidatus.

3.1 Paslėpti ketvertukai

Tobulas pavyzdys paslėptas ketvertas. [1,4,6,9 ] penktame kvadrate gali būti tik keturiose ląstelėse D4, D6, F4, F6. Vadovaudamiesi savo logika, pašaliname visus kitus kandidatus (pažymėtus geltonai).

4. „Ne guminis“

Jei kuris nors iš skaičių tame pačiame bloke (eilutė, stulpelis, kvadratas) pasirodo du ar tris kartus, galime pašalinti tą skaičių iš konjuguoto bloko. Yra keturi poravimo tipai:

1. Pora arba trys kvadrate - jei jie yra vienoje eilutėje, galite pašalinti visas kitas panašias reikšmes iš atitinkamos eilutės.
2. Pora arba Trys kvadrate – jei jie yra viename stulpelyje, visas kitas panašias reikšmes galite pašalinti iš atitinkamo stulpelio.
3. Pora arba trys iš eilės – jei jie yra tame pačiame kvadrate, visas kitas panašias reikšmes galite pašalinti iš atitinkamo kvadrato.
4. Pora arba Trys stulpelyje - jei jie yra tame pačiame kvadrate, galite pašalinti visas kitas panašias reikšmes iš atitinkamo kvadrato.

4.1 Rodyklės poros, trynukai

Leiskite parodyti jums šį galvosūkį kaip pavyzdį. Trečioje aikštėje 3 "yra tik viduje B7 Ir B9. Po pareiškimo №1 , pašaliname kandidatus iš B1, B2, B3. Taip pat, " 2 “ pašalina iš aštuntos aikštės galima prasmė iš G2.


Speciali dėlionė. Labai sunku išspręsti, bet jei atidžiai pažiūrėsite, galite pamatyti keletą rodyklių poros. Akivaizdu, kad ne visada būtina juos visus rasti, kad būtų pasiektas sprendimas, tačiau kiekvienas toks radinys palengvina mūsų užduotį.

4.2 Neredukuojamo mažinimas

Ši strategija apima kruopštų eilučių ir stulpelių analizavimą ir palyginimą su kvadratų turiniu (taisyklės №3 , №4 ).
Apsvarstykite liniją BET. "2 "įmanomi tik A4 Ir A5. laikantis taisyklės №3 , pašalinti " 2 " juos B5, C4, C5.


Ir toliau spręskime galvosūkį. Turime vieną vietą 4 "vieno kvadratinio colio atstumu 8 stulpelyje. Pagal taisyklę №4 , pašaliname nereikalingus kandidatus ir, be to, gauname sprendimą " 2 " dėl C7.

Pirmas dalykas, kuris turėtų būti nustatytas problemų sprendimo metodikoje, yra iš tikrųjų supratimas, ką mes pasiekiame ir galime pasiekti spręsdami problemas. Supratimas paprastai suvokiamas kaip savaime suprantamas dalykas, ir mes pamirštame, kad supratimas turi tam tikrą supratimo pradžios tašką, tik jo atžvilgiu galime teigti, kad supratimas iš tikrųjų vyksta nuo konkretaus mūsų nustatyto momento. Sudoku čia, mūsų nuomone, yra patogus tuo, kad leidžia, remiantis jo pavyzdžiu, tam tikru mastu modeliuoti problemų supratimo ir sprendimo problemas. Tačiau pradėsime nuo kelių kitų ir ne mažiau svarbių pavyzdžių nei Sudoku.

Fizikas, studijuojantis specialųjį reliatyvumą, gali kalbėti apie Einšteino „krištolo skaidrumo“ teiginius. Šią frazę aptikau vienoje iš interneto svetainių. Bet kur prasideda šis „kristalinio aiškumo“ supratimas? Tai prasideda nuo mokymosi matematinis žymėjimas postulatai, iš kurių pagal žinomas ir suprantamas taisykles gali būti pastatytos visos daugiaaukštės SRT matematinės konstrukcijos. Bet fizikas, kaip ir aš, nesupranta, kodėl SRT postulatai veikia taip, o ne kitaip.

Visų pirma, didžioji dauguma diskutuojančių apie šią doktriną nesupranta, kas tiksliai slypi šviesos greičio pastovumo postulate, verčiant nuo jos matematinio pritaikymo prie tikrovės. Ir šis postulatas reiškia šviesos greičio pastovumą visomis įmanomomis ir neįsivaizduojamomis prasmėmis. Šviesos greitis yra pastovus, palyginti su bet kuriais tuo pačiu metu ilsisinčiais ir judančiais objektais. Šviesos pluošto greitis, anot postulato, yra pastovus net artėjančio, skersinio ir tolstančio šviesos pluošto atžvilgiu. Ir tuo pačiu iš tikrųjų mes turime tik matavimus, kurie yra netiesiogiai susiję su šviesos greičiu, interpretuojami kaip jo pastovumas.

Niutono dėsniai fizikui ir net tiems, kurie tiesiog studijuoja fiziką, yra tokie žinomi, kad atrodo taip suprantami kaip savaime suprantamas dalykas, ir kitaip negali būti. Bet, tarkime, įstatymo taikymas gravitacija prasideda jo matematiniu žymėjimu, pagal kurį galima apskaičiuoti net kosminių objektų trajektorijas ir orbitų charakteristikas. Bet kodėl šie įstatymai veikia taip, o ne kitaip – ​​tokio supratimo neturime.

Panašiai ir su Sudoku. Internete galima rasti ne kartą pasikartojančių „pagrindinių“ Sudoku problemų sprendimo būdų aprašymų. Jei prisimenate šias taisykles, galite suprasti, kaip ta ar kita „Sudoku“ problema išsprendžiama taikydami „pagrindines“ taisykles. Bet mano klausimas toks: ar mes suprantame, kodėl šie „pagrindiniai“ metodai veikia taip, o ne kitaip.

Taigi pereiname prie kito rakto padėtis problemų sprendimo metodikoje. Suprasti galima tik remiantis kokiu nors modeliu, kuris suteikia pagrindą šiam supratimui ir gebėjimui atlikti kokį nors natūralų ar minties eksperimentą. Be to, mes galime turėti tik išmoktų atspirties taškų taikymo taisykles: SRT postulatus, Niutono dėsnius arba „pagrindinius“ Sudoku būdus.

Neturime ir iš esmės negalime turėti modelių, kurie tenkintų neribotos šviesos greičio pastovumo postulatą. Mes to nedarome, bet galima sugalvoti neįrodomus modelius, atitinkančius Niutono dėsnius. Ir tokių „niutoniškų“ modelių yra, bet jie kažkaip nežavi produktyviomis galimybėmis atlikti plataus masto ar minties eksperimentą. Tačiau Sudoku suteikia mums galimybių, kurias galime panaudoti norėdami suprasti tikrąsias Sudoku problemas ir iliustruoti modeliavimą kaip bendrą problemų sprendimo būdą.

Vienas iš galimų Sudoku problemų modelių yra darbalapis. Jis sukuriamas tiesiog užpildant visus tuščius užduotyje nurodytos lentelės langelius (ląsteles) skaičiais 123456789. Tada užduotis redukuojama iki nuoseklaus visų papildomų skaitmenų pašalinimo iš langelių, kol bus užpildyti visi lentelės langeliai. su pavieniais (išskirtiniais) skaitmenimis, atitinkančiais problemos sąlygą.

Kuriu tokį darbalapį „Excel“. Pirmiausia pasirenku visus tuščius lentelės langelius (ląsteles). Paspaudžiu F5 - "Pasirinkti" - "Tušti langeliai" - "Gerai". Bendresnis būdas pasirinkti norimus langelius: laikykite nuspaudę Ctrl ir spustelėkite pelę, kad pasirinktumėte šias ląsteles. Tada pasirinktoms ląstelėms aš nustatau mėlyna spalva, 10 dydis (originalas - 12) ir šriftas Arial Narrow. Visa tai daroma tam, kad vėlesni lentelės pakeitimai būtų aiškiai matomi. Toliau aš įeinu tuščios ląstelės numeriai 123456789. Darau taip: užsirašau ir išsaugau šį skaičių atskirame langelyje. Tada paspaudžiu F2, pasirenku ir nukopijuoju šį skaičių su Ctrl + C operacija. Toliau einu į lentelės langelius ir, nuosekliai apeidamas visus tuščius langelius, Ctrl + V operacija įvedu į juos skaičių 123456789, ir darbalapis paruoštas.

Papildomus skaičius, apie kuriuos bus kalbama vėliau, ištrinu taip. Su operacija Ctrl + pelės paspaudimas - aš parenku langelius su papildomu skaičiumi. Tada paspaudžiu Ctrl + H ir viršutiniame atsidariusio lango laukelyje įvedu numerį, kurį norite ištrinti, o apatinis laukas turi būti visiškai tuščias. Tada belieka spustelėti parinktį „Pakeisti viską“ ir papildomas numeris pašalinamas.

Sprendžiant iš to, kad man įprastais „baziniais“ būdais dažniausiai pavyksta atlikti pažangesnį lentelių apdorojimą nei internete pateiktuose pavyzdžiuose, darbalapis yra labiausiai paprastas įrankis sprendžiant Sudoku problemas. Be to, daugelio situacijų, susijusių su sudėtingiausių vadinamųjų „pagrindinių“ taisyklių taikymu, mano darbalapyje tiesiog nebuvo.

Tuo pačiu metu darbalapis taip pat yra modelis, pagal kurį galima atlikti eksperimentus, vėliau nustatant visas „pagrindines“ taisykles ir įvairius jų taikymo niuansus, kylančius iš eksperimentų.

Taigi, prieš jus yra darbalapio fragmentas su devyniais blokais, sunumeruotais iš kairės į dešinę ir iš viršaus į apačią. Šiuo atveju turime ketvirtą bloką, užpildytą skaičiais 123456789. Tai mūsų modelis. Už bloko ribų raudonai paryškinome „suaktyvintus“ (galiausiai apibrėžtus) skaičius, šiuo atveju keturis, kuriuos ketiname pakeisti rengiamoje lentelėje. Mėlynieji penketukai yra skaičiai, kurie dar nėra apibrėžti dėl savo būsimo vaidmens, apie kurį kalbėsime vėliau. Mūsų priskirti aktyvuoti numeriai tarsi išbraukiami, išstumiami, ištrinami – apskritai jie bloke išstumia tuos pačius numerius, todėl ten pavaizduoti blyškia spalva, simbolizuojančia faktą, kad šie blyškūs skaičiai buvo ištrintas. Šią spalvą norėjau padaryti dar blyškesnę, bet tada jos pasižiūrėjus internete galėjo tapti visiškai nematomos.

Dėl to ketvirtame bloke, langelyje E5, buvo vienas, taip pat aktyvuotas, bet paslėptas keturi. „Suaktyvinta“, nes ji savo ruožtu taip pat gali pašalinti papildomus skaitmenis, jei jie yra pakeliui, ir „paslėpta“, nes ji yra tarp kitų skaitmenų. Jei ląstelę E5 užpuola likusieji, išskyrus 4, aktyvuoti numeriai 12356789, tai E5 – 4 atsiras „nuogas“ vienišas.

Dabar pašalinkime vieną aktyvuotą ketvertą, pavyzdžiui, iš F7. Tada užpildytame bloke keturi gali būti jau ir tik langelyje E5 arba F5, o aktyvuoti 5 eilutėje. Jei šioje situacijoje dalyvauja aktyvuoti penketukai, be F7=4 ir F8=5, tai langeliuose E5 ir F5 ten yra bus nuoga arba paslėpta aktyvuota pora 45.

Po to, kai pakankamai pasidarbavote ir supratote skirtingi variantai su nuogais ir pasislėpusiais viengungiais, dviese, trise ir pan. ne tik blokais, bet ir eilutėmis bei stulpeliais galime pereiti prie kito eksperimento. Sukurkime pliką porą 45, kaip darėme anksčiau, o tada sujungsime aktyvuotus F7=4 ir F8=5. Dėl to susiklostys situacija E5=45. Panašios situacijos labai dažnai susidaro apdorojant darbalapį. Ši situacija reiškia, kad vienas iš šių skaitmenų, šiuo atveju 4 arba 5, būtinai turi būti bloke, eilutėje ir stulpelyje, kuriame yra langelis E5, nes visais šiais atvejais turi būti du skaitmenys, o ne vienas iš jų.

Ir, svarbiausia, dabar jau žinome, kaip dažnai pasitaiko tokios situacijos kaip E5=45. Panašiai apibrėšime situacijas, kai viename langelyje atsiranda trigubas skaitmenų ir pan. Ir kai šių situacijų supratimo ir suvokimo laipsnį perkelsime į savaime suprantamą ir paprastumą, tada kitas žingsnis yra, taip sakant, mokslinis situacijų supratimas: tada galėsime atlikti statistinę Sudoku lenteles, identifikuokite modelius ir naudokite sukauptą medžiagą, kad išspręstumėte daugiausiai sunkiausias užduotis.

Taigi, eksperimentuodami su modeliu, gauname vizualų ir net „mokslinį“ paslėptų ar atvirų singlų, porų, trigubų ir kt. Jei apsiribosite operacijomis su aprašytu paprastu modeliu, kai kurios jūsų idėjos pasirodys netikslios ar net klaidingos. Tačiau kai tik pasieksite sprendimą konkrečias užduotis, tuomet greitai išaiškės pirminių idėjų netikslumai, tačiau modelius, kuriais remiantis buvo atlikti eksperimentai, teks permąstyti ir patobulinti. Tai neišvengiamas hipotezių ir patikslinimų kelias sprendžiant bet kokias problemas.

Turiu pasakyti, kad paslėpti ir atviri pavieniai, taip pat atviros poros, trigubai ir net ketvertukai yra dažnos situacijos, kylančios sprendžiant Sudoku problemas su darbalapiu. Paslėptos poros buvo retos. O štai paslėpti trigubai, ketvertukai ir t.t. Aš kažkaip nesusidūriau apdorojant darbalapius, kaip ir internete ne kartą aprašytus „x-wing“ ir „kardžuvės“ kontūrų apėjimo būdus, kuriuose yra „kandidatų“ ištrinti su bet kuriuo iš du alternatyvūs kontūrų apėjimo būdai. Šių metodų prasmė: jei sunaikiname "kandidatą" x1, tai lieka išskirtinis kandidatas x2 ir tuo pačiu kandidatas x3 išbraukiamas, o jei sunaikiname x2, lieka išskirtinis x1, bet šiuo atveju kandidatas x3 taip pat ištrintas, todėl bet kuriuo atveju x3 turėtų būti ištrintas , kol kas tai nepaveiks kandidatų x1 ir x2. Daugiau bendrasis planas, tai ypatinga byla situacijos: jei du alternatyvių būdų pasiekti tą patį rezultatą, tada šis rezultatas gali būti naudojamas sprendžiant Sudoku problemą. Šioje, bendresnėje, situacijoje sutikau situacijų, bet ne „x-wing“ ir „swordfish“ variantuose, o ne sprendžiant Sudoku uždavinius, kuriems pakanka žinių tik apie „bazinius“ metodus.

Darbalapio naudojimo ypatybės gali būti parodytos toliau pateiktame nereikšmingame pavyzdyje. Viename iš sudoku sprendimų forumų http://zforum.net/index.php?topic=3955.25;wap2 aptikau problemą, pateiktą kaip viena iš sudėtingiausių sudoku problemų, kurios negalima išspręsti įprastais būdais, nenaudojant išvardijimo prielaidos apie skaičius, pakeistus langeliuose. Parodykime, kad su darbo lentele galima išspręsti šią problemą be tokio išvardinimo:

Dešinėje – pirminė užduotis, kairėje – darbo lentelė po „ištrynimo“, t.y. įprastinė papildomų skaitmenų pašalinimo operacija.

Pirmiausia susitarkime dėl žymėjimo. ABC4=689 reiškia, kad langeliuose A4, B4 ir C4 yra skaičiai 6, 8 ir 9 – po vieną ar daugiau skaitmenų kiekviename langelyje. Tas pats ir su stygomis. Taigi B56=24 reiškia, kad langeliuose B5 ir B6 yra skaičiai 2 ir 4. Ženklas ">" yra sąlyginio veiksmo ženklas. Taigi D4=5>I4-37 reiškia, kad dėl pranešimo D4=5 langelyje I4 turėtų būti įrašytas skaičius 37. Žinia gali būti atvira – „nuoga“ – ir paslėpta, kuri turėtų būti atskleista. Pranešimo poveikis gali būti nuoseklus (netiesiogiai perduodamas) išilgai grandinės ir lygiagretus (veikti tiesiogiai kitus langelius). Pavyzdžiui:

D3=2; D8=1>A9-1>A2-2>A3-4,G9-3; (D8=1)+(G9=3)>G8-7>G7-1>G5-5

Šis įrašas reiškia, kad D3=2, tačiau šį faktą reikia atskleisti. D8=1 perduoda savo veiksmą grandinėje į A3, o 4 turi būti parašytas į A3; tuo pačiu metu D3=2 veikia tiesiogiai G9, todėl G9-3. (D8=1)+(G9=3)>G8-7 – bendra veiksnių (D8=1) ir (G9=3) įtaka lemia rezultatą G8-7. ir kt.

Įrašuose taip pat gali būti H56/68 tipo derinys. Tai reiškia, kad langeliuose H5 ir H6 draudžiami skaičiai 6 ir 8, t.y. juos reikia pašalinti iš šių ląstelių.

Taigi, pradedame dirbti su lentele ir pradžiai pritaikome gerai išreikštą, pastebimą sąlygą ABC4=689. Tai reiškia, kad visose kitose (išskyrus A4, B4 ir C4) 4 bloko (viduryje, kairėje) ir 4 eilutės langeliuose skaičiai 6, 8 ir 9 turėtų būti ištrinti:

B56=24 taikyti lygiai taip pat. Kartu turime D4=5 ir (po D4=5>I4-37) HI4=37, taip pat (po B56=24>C6-1) C6=1. Taikykime tai darbalapiui:

I89=68paslėptas>I56/68>H56-68: t.y. langeliuose I8 ir I9 yra paslėpta 5 ir 6 skaitmenų pora, kuri draudžia šiems skaitmenims būti I56, todėl gaunamas rezultatas H56-68. Šį fragmentą galime vertinti kitaip, kaip ir eksperimentuodami su darbalapio modeliu: (G23=68)+(AD7=68)>I89-68; (I89=68)+(ABC4=689)>H56-68. Tai yra, dvipusis „ataka“ (G23=68) ir (AD7=68) veda prie to, kad I8 ir I9 gali būti tik skaičiai 6 ir 8. Toliau (I89=68) yra prijungtas prie „ ataka“ prieš H56 kartu su ankstesnėmis sąlygomis, o tai veda į H56-68. Be šios „atakos“ yra prijungtas (ABC4=689), kuris į šis pavyzdys atrodo perteklinis, bet jei dirbtume be darbalapio, tai smūgio koeficientas (ABC4=689) būtų paslėptas, į jį derėtų atkreipti ypatingą dėmesį.

Kitas veiksmas: I5=2>G1-2,G6-9,B6-4,B5-2.

Tikiuosi, jau aišku be komentarų: pakeiskite skaičius, esančius po brūkšnio, nesuklysite:

H7=9>I7-4; D6=8>D1-4,H6-6>H5-8:

Kita veiksmų serija:

D3=2; D8=1>A9-1>A2-2>A3-4,G9-3;

(D8=1)+(G9=3)>G8-7>G7-1>G5-5;

D5=9>E5-6>F5-4:

I=4>C9-4>C7-2>E9-2>EF7-35>B7-7, F89-89,

tai yra, dėl „perbraukimo“ – ištrynus papildomus skaitmenis – langeliuose F8 ir F9 atsiranda atvira, „nuoga“ pora 89, kurią kartu su kitais įraše nurodytais rezultatais taikome lentelei:

H2=4>H3-1>F2-1>F1-6>A1-3>B8-3,C8-5,H1-7>I2-5>I3-3>I4-7>H4-3

Jų rezultatas:

Po to seka gana įprasti, akivaizdūs veiksmai:

H1=7>C1-8>E1-5>F3-7>E2-9>E3-8,C3-9>B3-5>B2-6>C2-7>C4-6>A4-9>B4- 8;

B2=6>B9-9>A8-6>I8-8>F8-9>F9-8>I9-6;

E7=3>F7-5,E6-7>F6-3

Jų rezultatas: galutinis problemos sprendimas:

Vienaip ar kitaip, manysime, kad „pagrindinius“ metodus „Sudoku“ ar kitose intelektualinio pritaikymo srityse išsiaiškinome pagal tam tinkamą modelį ir net išmokome juos taikyti. Tačiau tai tik dalis mūsų pažangos problemų sprendimo metodikos srityje. Be to, kartoju, į tai ne visada atsižvelgiama, bet tai yra būtinas etapas, siekiant palengvinti anksčiau išmoktus metodus. Spręsti pavyzdžius, suvokti šio sprendimo rezultatus ir metodus, permąstyti šią medžiagą remiantis priimtu modeliu, dar kartą apgalvoti visas galimybes, priartinti jų supratimo laipsnį į automatizavimą, kai sprendimas naudojant „pagrindines“ nuostatas tampa įprastas. ir išnyksta kaip problema. Ką tai duoda: kiekvienas turėtų tai pajusti savo patirtimi. O esmė ta, kad probleminei situacijai tapus rutina, intelekto paieškos mechanizmas nukreipiamas į vis sudėtingesnių nuostatų kūrimą sprendžiamų problemų srityje.

O kas yra „sudėtingesnės nuostatos“? Tai tik naujos „pagrindinės“ nuostatos sprendžiant problemą, kurių supratimas, savo ruožtu, taip pat gali būti supaprastintas, jei randamas tam tikslui tinkamas modelis.

Straipsnyje Vasilenko S.L. „Numeric Harmony Sudoku“ randu 18 simetriškų klavišų problemos pavyzdį:

Kalbant apie šią užduotį, teigiama, kad ji gali būti išspręsta naudojant „pagrindinius“ metodus tik iki tam tikros būsenos, kurią pasiekus belieka taikyti paprastą surašymą su bandomuoju pakaitalu į kokio nors tariamo išskirtinio (viengubo, viengubo) ląsteles. ) skaitmenys. Ši būsena (šiek tiek toliau nei Vasilenko pavyzdyje) atrodo taip:

Yra toks modelis. Tai tam tikras identifikuotų ir neatpažintų išskirtinių (vieno) skaitmenų sukimosi mechanizmas. Paprasčiausiu atveju koks nors trigubas išskirtinių skaitmenų sukasi dešine arba kaire kryptimi, eidamas pro šią grupę iš eilutės į eilutę arba iš stulpelio į stulpelį. Apskritai, tuo pačiu metu viena kryptimi sukasi trys skaičių trigubų grupės. Daugiau sunkių atvejų, trys išskirtinių skaitmenų poros sukasi viena kryptimi, o trigubas skaitmenų sukasi priešinga kryptimi. Taigi, pavyzdžiui, išskirtiniai skaitmenys pirmose trijose nagrinėjamos problemos eilutėse yra pasukami. Ir, svarbiausia, tokį sukimąsi galima pamatyti įvertinus skaičių vietą apdorotame darbalapyje. Šios informacijos kol kas pakanka, o kitus sukimosi modelio niuansus suprasime problemos sprendimo procese.

Taigi pirmose (viršutinėse) trijose eilutėse (1, 2 ir 3) galime pastebėti porų (3+8) ir (7+9), taip pat (2+x1) su nežinomu x1 ir singlų trigubas (x2+4+ 1) su nežinomu x2. Tai darydami galime pastebėti, kad kiekvienas iš x1 ir x2 gali būti 5 arba 6.

4, 5 ir 6 eilutėse apžvelgiamos poros (2+4) ir (1+3). Taip pat turėtų būti 3-ioji nežinoma pora ir trigubas singlų, iš kurių žinomas tik vienas skaitmuo 5.

Panašiai žiūrime į 789 eilutes, tada į stulpelių ABC, DEF ir GHI trejetus. Surinktą informaciją surašysime simboline ir, tikiuosi, visai suprantama forma:

Kol kas šios informacijos mums reikia tik bendrai situacijai suprasti. Atidžiai pagalvokite ir tada pereisime prie šios specialiai tam paruoštos lentelės:

Alternatyvas išryškinau spalvomis. Mėlyna reiškia „leidžiama“, o geltona – „draudžiama“. Jei, tarkime, leidžiama A2=79 leidžiama A2=7, tai C2=7 draudžiama. Arba atvirkščiai – leidžiama A2=9, draudžiama C2=9. Ir tada leidimai ir draudimai perduodami logine grandine. Šis dažymas atliekamas tam, kad būtų lengviau peržiūrėti įvairias alternatyvas. Apskritai, tai yra tam tikra analogija su „x-wing“ ir „swordfish“ metodais, minėtais apdorojant lenteles.

Žvelgiant į B6=7 ir atitinkamai B7=9 parinktis, iškart galime rasti du su šia galimybe nesuderinamus taškus. Jei B7=9, tai 789 eilutėse atsiranda sinchroniškai besisukantis trigubas, o tai nepriimtina, nes sinchroniškai (viena kryptimi) gali suktis arba tik trys poros (ir joms asinchroniškai trys pavieniai), arba trys trigubai (be pavienių). Be to, jei B7=9, tai po kelių žingsnių apdorojant darbalapį 7 eilutėje rasime nesuderinamumą: B7=D7=9. Taigi mes pakeičiame vienintelį priimtiną iš dviejų alternatyva B6=9, tada problema išspręsta paprastos priemonėsįprastas apdorojimas be jokio aklo išvardijimo:

Kitas, aš turiu baigtas pavyzdys naudojant sukimosi modelį pasaulio sudoku čempionato problemai išspręsti, bet šį pavyzdį praleidžiu, kad per daug neištempčiau šio straipsnio. Be to, kaip paaiškėjo, ši problema turi tris sprendimus, kurie menkai tinka pirminiam skaitmenų sukimosi modelio kūrimui. Taip pat daug pūpsojau apie Gary'io McGuire'o 17 raktų problemą, ištrauktą iš interneto, kad išspręsčiau jo galvosūkį, kol dar labiau susierzinęs sužinojau, kad ši „dėlionė“ turi daugiau nei 9 tūkstančius sprendimų.

Taigi, norom nenorom tenka pereiti prie Arto Inkalos sukurtos „sunkiausios pasaulyje“ Sudoku problemos, kuri, kaip žinia, turi unikalų sprendimą.

Įvedus du gana akivaizdžius išskirtinius skaičius ir apdorojus darbalapį, užduotis atrodo taip:

Klavišai nustatyti juodai ir didesniu šriftu originali problema. Norėdami eiti į priekį sprendžiant šią problemą, vėl turime pasikliauti tinkamu modeliu, tinkamu šiam tikslui. Šis modelis yra savotiškas skaičių sukimosi mechanizmas. Tai jau ne kartą buvo aptarta šiame ir ankstesniuose straipsniuose, tačiau norint suprasti tolesnę straipsnio medžiagą, šis mechanizmas turėtų būti apgalvotas ir išsamiai išdirbtas. Maždaug taip, lyg su tokiu mechanizmu būtum dirbęs dešimt metų. Bet jūs vis tiek galėsite suprasti šią medžiagą, jei ne iš pirmo skaitymo, tai iš antro ar trečio ir pan. Be to, jei atkakliai atkakliai, šią „sunkiai suprantamą“ medžiagą paversi įprasta ir paprastumo būseną. Šiuo atžvilgiu nėra nieko naujo: kas iš pradžių labai sunku, pamažu tampa nebe taip sunku, o toliau nenutrūkstamai tobulėjant viskas tampa akivaizdžiausia ir nereikalauja protinių pastangų į savo vietą, po kurios gali išlaisvinti savo protą. tolesnės pažangos sprendžiamos problemos ar kitų problemų atveju.

Kruopšti Arto Incal problemos struktūros analizė rodo, kad visa problema paremta trijų sinchroniškai besisukančių porų ir trigubo asinchroniškai besisukančių pavienių porų principu: (x1+x2)+(x3+x4)+(x5+) x6)+(x7+x8+ x9). Sukimo tvarka gali būti, pavyzdžiui, tokia: pirmose trijose eilutėse 123 pirmoji pora (x1+x2) eina iš pirmo bloko pirmos eilutės į antrą antrojo bloko eilutę, tada į trečią eilutę. trečiojo bloko. Antroji pora peršoka iš pirmo bloko antrosios eilės į antrojo bloko trečią eilę, tada šioje sukimosi metu peršoka į trečio bloko pirmąją eilę. Trečioji pora iš trečios pirmojo bloko eilės peršoka į antrojo bloko pirmąją eilutę, o tada ta pačia sukimosi kryptimi peršoka į trečiojo bloko antrąją eilę. Pavienių asmenų trijulė juda panašia sukimosi schema, bet priešinga kryptimi nei poros. Situacija su stulpeliais atrodo panašiai: jei lentelė mintyse (ar iš tikrųjų) pasukta 90 laipsnių, tada eilutės taps stulpeliais, kurių pavienių ir porų judėjimo pobūdis bus toks pat, kaip ir anksčiau eilėms.

Mintyse apversdami šiuos sukimus, susijusius su Arto Incal problema, pamažu suprantame akivaizdžius apribojimus renkantis šio sukimo variantus pasirinktam trigubui eilučių ar stulpelių:

Neturėtų būti sinchroniškai (viena kryptimi) besisukančių trigubų ir porų – tokie trigubai, priešingai nei pavienių trigubai, ateityje bus vadinami trejetais;

Neturėtų būti asinchroninių tarpusavyje porų arba asinchroninių vienas su kitu;

Neturėtų būti ir porų, ir pavienių, besisukančių ta pačia (pavyzdžiui, dešine) kryptimi – tai ankstesnių apribojimų pakartojimas, bet gali atrodyti suprantamiau.

Be to, yra ir kitų apribojimų:

9 eilutėse neturi būti nė vienos poros, kuri atitiktų porą nė viename iš stulpelių, o stulpeliams ir eilutėms – tokia pati. Tai turėtų būti akivaizdu: nes pats faktas, kad du skaičiai yra toje pačioje eilutėje, rodo, kad jie yra skirtinguose stulpeliuose.

Taip pat galima sakyti, kad labai retai pasitaiko porų atitikmenų skirtinguose eilučių trigubuose arba panašios atitikties trijuose stulpelių, taip pat retai pasitaiko pavienių triviečių atitikmenų eilutėse ir (arba) stulpeliuose, bet tai, taip sakant, , tikimybiniai modeliai.

Tyrimo blokai 4,5,6.

4-6 blokuose galimos poros (3+7) ir (3+9). Jei priimame (3+9), tai gauname neteisingą sinchroninį tripleto sukimąsi (3+7+9), taigi turime porą (7+3). Pakeitus šią porą ir vėliau apdorojus lentelę įprastomis priemonėmis, gauname:

Tuo pačiu galime teigti, kad 5 B6=5 gali būti tik vienišas, asinchroninis (7+3), o 6 I5=6 yra parageneratorius, nes yra toje pačioje eilutėje H5=5 šeštoje. blokas, todėl jis negali būti vienas ir gali judėti tik sinchroniškai su (7+3.

ir suskirstė kandidatus į vienišius pagal jų pasirodymų skaičių šioje lentelėje:

Jei priimtume, kad dažniausiai 2, 4 ir 5 yra pavieniai, tai pagal sukimosi taisykles su jais gali būti derinamos tik poros: (7 + 3), (9 + 6) ir (1 + 8) - a. pora (1 + 9) atmesta, nes ji paneigia porą (9 + 6). Be to, pakeitus šias poras ir pavienius ir tolesnis apdorojimas lenteles įprastais metodais gauname:

Pasirodė tokia nepaklusni lentelė – jos nesinori apdoroti iki galo.

Teks pasistengti ir pastebėti, kad ABC stulpeliuose yra pora (7 + 4) ir 6 juda sinchroniškai su 7 šiuose stulpeliuose, todėl 6 yra poravimas, todėl stulpelyje galimi tik deriniai (6 + 3). 4 bloko „C“ +8 arba (6+8)+3. Pirmoji iš šių kombinacijų neveikia, nes tuomet 7-ame bloke stulpelyje „B“ atsiras netinkamas sinchroninis trigubas – tripletas (6 + 3 + 8). Na, o tada, pakeitę variantą (6 + 8) + 3 ir įprastu būdu apdoroję lentelę, pasiekiame sėkmingą užduoties atlikimą.

Antrasis variantas: grįžkime prie lentelės, gautos identifikavus kombinaciją (7 + 3) + 5 456 eilutėse ir pereikime prie stulpelių ABC tyrimo.

Čia galime pastebėti, kad pora (2+9) negali vykti ABC. Kiti deriniai (2+4), (2+7), (9+4) ir (9+7) duoda sinchroninį trigubą – tripletą A4+A5+A6 ir B1+B2+B3, o tai nepriimtina. Lieka viena priimtina pora (7+4). Be to, 6 ir 5 sinchroniškai juda 7, vadinasi, jie yra garą formuojantys, t.y. sudaryti kelias poras, bet ne 5 + 6.

Sudarykime galimų porų ir jų derinių su pavieniais sąrašą:

Derinys (6+3)+8 neveikia, nes kitu atveju viename stulpelyje (6+3+8) susidaro negaliojantis trejetas-tripletas, kuris jau buvo aptartas ir kurį dar kartą galime patikrinti patikrinę visus variantus. Iš kandidatų į vienvietes daugiausiai balų surenka 3 skaičius, o iš visų minėtų kombinacijų greičiausiai: (6 + 8) + 3, t.y. (C4=6 + C5=8) + C6=3, todėl gaunama:

Be to, labiausiai tikėtinas kandidatas į vienišius yra 2 arba 9 (po 6 balus), tačiau bet kuriuo iš šių atvejų 1 kandidatas (4 balai) lieka galioti. Pradėkime nuo (5+29)+1, kur 1 yra asinchroninis su 5, t.y. Įdėkite 1 iš B5=1 kaip asinchroninį vienetą visuose ABC stulpeliuose:

7 bloko A stulpelyje galimi tik variantai (5+9)+3 ir (5+2)+3. Bet geriau atkreipti dėmesį į tai, kad 1-3 eilutėse dabar atsirado poros (4 + 5) ir (8 + 9). Jų pakeitimas lemia greitą rezultatą, t.y. iki užduoties atlikimo po to, kai lentelė buvo apdorota įprastomis priemonėmis.

Na, o dabar, pasipraktikavę su ankstesniais variantais, galime pabandyti išspręsti Arto Incal problemą nenaudodami statistinių įverčių.

Vėl grįžtame į pradinę padėtį:

4-6 blokuose galimos poros (3+7) ir (3+9). Jei priimame (3 + 9), gauname neteisingą sinchroninį tripleto sukimąsi (3 + 7 + 9), todėl lentelėje turime tik parinktį (7 + 3):

5 čia, kaip matome, yra vienišas, 6 yra paraformeris. Galiojančios parinktys ABC5: (2+1)+8, (2+1)+9, (8+1)+9, (8+1)+2, (9+1)+8, (9+1) +2. Bet (2+1) yra asinchroninis su (7+3), todėl yra (8+1)+9, (8+1)+2, (9+1)+8, (9+1)+2. Bet kuriuo atveju 1 yra sinchroninis (7 + 3) ir todėl parageneruojantis. Pakeiskime 1 šioje lentelėje lentelėje:

Skaičius 6 čia yra parageneratorius bl. 4-6, tačiau ryškios poros (6+4) galiojančių porų sąraše nėra. Taigi keturkampis A4 = 4 yra asinchroninis 6:

Kadangi D4+E4=(8+1) ir pagal sukimosi analizę sudaro šią porą, gauname:

Jei langeliai C456=(6+3)+8, tai B789=683, t.y. gauname sinchroninį trigubą-tripletą, todėl lieka parinktis (6+8)+3 ir jos pakeitimo rezultatas:

B2=3 čia yra vienas, C1=5 (asinchroninis 3) yra poravimas, A2=8 taip pat yra poravimas. B3=7 gali būti ir sinchroninis, ir asinchroninis. Dabar galime įrodyti save sudėtingesniais triukais. Išlavinta akimi (ar bent jau tikrinant kompiuteriu) matome, kad esant bet kokiai būsenai B3=7 – sinchroninė ar asinchroninė – gauname tą patį rezultatą A1=1. Todėl mes galime pakeisti šią reikšmę į A1 ir tada atlikti savo, tiksliau Arto Incala, užduotį įprastesnėmis paprastomis priemonėmis:

Vienaip ar kitaip, galėjome apsvarstyti ir net iliustruoti tris bendrus problemų sprendimo būdus: nustatyti problemos supratimo tašką (ne hipotetinį ar aklai deklaruotą, o realų momentą, nuo kurio galima kalbėti apie problemos supratimą). ), pasirinkite modelį, leidžiantį suvokti supratimą per natūralų ar psichinį eksperimentą ir, trečia, šiuo atveju pasiektų rezultatų supratimo ir suvokimo laipsnį perkelti į savaime suprantamą ir paprastumą. Taip pat yra ketvirtasis metodas, kurį aš asmeniškai naudoju.

Kiekvienas žmogus turi būsenų, kai jam kylančios intelektualinės užduotys ir problemos išsprendžiamos lengviau nei paprastai. Šios būsenos yra gana atkuriamos. Norėdami tai padaryti, turite įvaldyti minčių išjungimo techniką. Iš pradžių bent sekundės dalelę, vėliau vis labiau tempiant šį atsijungimo momentą. Daugiau nieko negaliu pasakyti, tiksliau, rekomenduoti, nes šio metodo taikymo trukmė yra grynai asmeninis reikalas. Tačiau šio metodo griebiausi kartais ilgai, kai prieš akis iškyla problema, prie kurios nematau variantų, kaip prie jos privažiuoti ir ją išspręsti. Dėl to iš atminties saugyklų anksčiau ar vėliau išnyra tinkamas modelio prototipas, kuris išaiškina esmę, ką reikia išspręsti.

Inkalo problemą išsprendžiau keliais būdais, įskaitant aprašytus ankstesniuose straipsniuose. Ir visada vienaip ar kitaip taikiau šį ketvirtąjį metodą su išsijungimu ir vėlesniu protinių pastangų sutelkimu. Greičiausią problemos sprendimą gavau paprastu išvardinimu – vadinamuoju „kišimo metodu“, tačiau naudodamas tik „ilgas“ parinktis: tokias, kurios gali greitai lemti teigiamą arba neigiamą rezultatą. Kiti variantai iš manęs atėmė daugiau laiko, nes didžioji laiko dalis buvo skirta bent apytikriai šių parinkčių taikymo technologijos kūrimui.

Geras pasirinkimas taip pat yra ketvirtojo požiūrio dvasia: prisijunkite prie Sudoku problemų sprendimo, sprendžiant problemą pakeičiant tik vieną skaitmenį kiekvienoje langelyje. Tai yra, didžioji dalis užduoties ir jos duomenų yra „slenkama“ mintyse. Tai yra pagrindinė intelektualinio problemų sprendimo proceso dalis, todėl šį įgūdį reikia lavinti, kad padidėtų jūsų gebėjimas spręsti problemas. Pavyzdžiui, nesu profesionalus Sudoku sprendėjas. Turiu kitų užduočių. Tačiau vis dėlto noriu išsikelti sau tokį tikslą: įgyti galimybę išspręsti padidinto sudėtingumo Sudoku problemas be darbalapio ir nekeičiant daugiau nei vieno skaičiaus į vieną tuščią langelį. Šiuo atveju leidžiamas bet koks Sudoku sprendimo būdas, įskaitant paprastą parinkčių sąrašą.

Neatsitiktinai prisimenu čia pateiktą variantų sąrašą. Bet koks Sudoku problemų sprendimo būdas apima tam tikrų metodų rinkinį savo arsenale, įskaitant vienokį ar kitokį surašymo tipą. Tuo pačiu metu bet kuris iš Sudoku naudojamų metodų arba sprendžiant bet kokias kitas problemas turi savo sritį. efektyvus taikymas. Taigi, sprendžiant paprastos užduotys Sudoku paprasti "pagrindiniai" metodai yra patys veiksmingiausi, aprašyti daugybėje straipsnių šia tema internete, o sudėtingesnis "sukimosi metodas" čia dažnai yra nenaudingas, nes jis tik apsunkina eigą. paprastas sprendimas ir tuo pačiu nesuteikia jokios naujos informacijos, kuri atsiranda sprendžiant problemą. Tačiau sunkiausiais atvejais, kaip Arto Incal problema, „sukimosi metodas“ gali atlikti pagrindinį vaidmenį.

Sudoku mano straipsniuose yra tik iliustruojantis problemų sprendimo būdų pavyzdys. Tarp mano išspręstų problemų taip pat yra daug sudėtingesnių nei Sudoku. Pavyzdžiui, esantis mūsų svetainėje kompiuterių modeliai katilų ir turbinų eksploatavimas. Aš irgi neprieštaraučiau apie juos kalbėti. Bet kol kas pasirinkau Sudoku, tad to užtenka vizualiai parodykite savo jauniesiems bendrapiliečiams galimi būdai ir pažangos žingsniai siekiant galutinio sprendžiamų problemų tikslo.

Tai viskas siandienai.

Sveiki! Šiame straipsnyje mes išsamiai išanalizuosime sudėtingo Sudoku sprendimą, naudodami konkretų pavyzdį. Prieš pradedant analizę, sutinkame mažuosius kvadratėlius vadinti skaičiais, numeruojant juos iš kairės į dešinę ir iš viršaus į apačią. Visi pagrindiniai Sudoku sprendimo principai aprašyti šiame straipsnyje.

Kaip įprasta, pirmiausia pažvelgsime į atvirus singlus. O tokių b5-5, e6-3 buvo tik du. Toliau į visus tuščius laukus pateikiame galimus kandidatus.

Kandidatai bus rašomi smulkiu šriftu žalia spalva atskirti nuo jau stovinčių skaitmenų. Mes tai darome mechaniškai, tiesiog surūšiuodami visas tuščias ląsteles ir įvesdami į juos skaičius, kurie gali būti juose.

Mūsų darbo vaisius galima pamatyti 2 paveiksle. Nukreipkime dėmesį į ląstelę f2. Ji turi du kandidatus 5 ir 9. Turėsime eiti su spėjimo metodu, o klaidos atveju grįžti prie šio pasirinkimo. Padėkime skaičių penktą. Išimkime penkis iš f eilutės, 2 stulpelio ir ketvirto kvadrato kandidatų.

Nustačius numerį nuolat šalinsime galimus kandidatus, o šiame straipsnyje į tai nebekreipiame dėmesio!

Toliau žiūrime į ketvirtą kvadratą, turime trišakį - tai langeliai e1, d2, e3, kuriuose yra 2, 8 ir 9 kandidatai. Išimkime juos iš likusių neužpildytų ketvirto kvadrato langelių. Pirmyn. Šeštajame kvadrate skaičius penki gali būti tik e8.

Daugiau apie Šis momentas nėra porų, trišakių, jau nekalbant apie ketvertus. Todėl eikime kitu keliu. Peržiūrėkime visas vertikalias ir horizontales, kad pašalintume nereikalingus kandidatus.

Ir taip antroje vertikalėje skaičius 8 gali būti tik langeliuose -h2 ir i2, išimkime aštuntą skaičių iš kitų neužpildytų septinto kvadrato langelių. Trečiajame faile skaičius aštuoni gali būti tik e3. Tai, ką gavome, parodyta 3 paveiksle.

Daugiau nėra už ko griebtis. Turime gana kietą riešutą, bet vis tiek jį sulaužysime! Taigi, dar kartą apsvarstykite mūsų porą e1 ir d2, sutvarkykite ją tokiu būdu d2-9, e1 -2. Ir mūsų klaidos atveju vėl grįšime prie šios poros.

Dabar galime saugiai įrašyti deuce į langelį d9! O aikštėje yra septyni, devyni gali būti tik ant h1. Po to ant vertikalios 1 penketukas gali būti tik ant i1, o tai savo ruožtu suteikia teisę dėti penketuką ant h9 langelio.

4 paveiksle parodyta, ką padarėme. Dabar apsvarstykite kitą porą, tai yra d3 ir f1. Jie turi kandidatus 7 ir 6. Žvelgiant į priekį pasakysiu, kad išdėstymo variantas d3-7, f1-6 yra klaidingas ir straipsnyje nesvarstysime, kad negaištume laiko.

5 paveiksle parodytas mūsų darbas. Ką mums belieka daryti toliau? Žinoma, dar kartą peržiūrėkite skaičių nustatymo parinktis! Į ląstelę g1 įdedame trigubą. Išsaugokite kaip visada, kad galėtumėte sugrįžti. Vienas yra nustatytas i3. dabar septintame kvadrate gauname porą h2 ir i2 su skaičiais 2 ir 8. Tai suteikia teisę neįtraukti šiuos skaičius iš visos neužpildytos vertikalės kandidatų.

Remdamiesi paskutine teze, sutvarkome. a2 yra keturi, b2 yra trys. Ir po to galime nuleisti visą pirmą kvadratą. c1 – šeši, a1 – vienas, b3 – devyni, c3 – du.

6 paveiksle parodyta, kas atsitiko. i5 turime paslėptą vienišį – numerį trys! Ir i2 gali turėti tik skaičių 2! Atitinkamai, h2–8.

Dabar pereikime prie langelių e4 ir e7, tai pora su kandidatais 4 ir 9. Sudėkime juos taip: e4 keturi, e7 devyni. Dabar šešetas dedamas ant f6, o devynetas – ant f5! Toliau c4 mes gauname paslėptą vienišį - numerį devyni! Ir mes galime iš karto įdėti keturis iš 8, o tada uždaryti horizontalią: c6 aštuoni.

SUDOKU yra populiarus dėlionės žaidimas, kuris yra skaičių galvosūkis, kurį galima įveikti tik padarius logiškas išvadas. Sudoku pavadinime, išvertus iš japonų kalbos, „su“ reiškia „skaičius“, o doku „doku“ reiškia „išsiskiriantis“. Todėl „SUDOKU“ apytiksliai reiškia „vieno skaitmens“.

Pavadinimą „Sudoku“ šiam galvosūkiui suteikė japonų leidėjas Nicoli 1984 m. Sudoku yra „Suuji wa dokushin ni kagiru“ santrumpa, kuri japonų kalba reiškia „turi būti tik vienas skaičius“. Leidykla „Nikoli“ ne tik sugalvojo skambų pavadinimą, bet ir pirmą kartą įvedė simetriją savo galvosūkių užduotyse. Dėlionės pavadinimą davė Nicoli lyderis Kaji Maki. Visas pasaulis priėmė šį naują japonišką pavadinimą, tačiau pačioje Japonijoje galvosūkis vadinamas „Nanpure“. Nicoli savo šalyje įregistravo žodį „Sudoku“ kaip prekės ženklą.

SUDOKU ištakos

Indija laikoma šachmatų gimtine, Anglija – futbolo gimtine. Sudoku žaidimas (sudoku), kuris greitai išplito visame pasaulyje, neturi tėvynės. Sudoku prototipu galima laikyti „Magic Square“ galvosūkį, kuris Kinijoje pasirodė prieš 2000 metų.

Sudoku, kaip žaidimo, istorija siekia garsųjį šveicarų matematiką, mechaniką ir fiziką Leonhardą Eulerį (1707–1783).

Jo archyve esančiuose dokumentuose, datuotuose 1776 m. spalio 17 d., yra pastabų, kaip suformuoti stebuklingą kvadratą su tam tikras skaičius langeliai, ypač 9, 16, 25 ir 36. Kitame dokumente pavadinimu " Moksliniai tyrimai naujos magiškojo kvadrato atmainos Euleris įdėtas į ląsteles laiškus(lot. kvadratas), vėliau jis užpildė langelius Graikiškos raidės ir pavadino aikštę graikų-lotynų kalba. Tyrinėjant įvairių variantų magiškas kvadratas, Euleris atkreipė dėmesį į simbolių jungimo problemą taip, kad nė vienas iš jų nepasikartotų jokioje eilutėje ir jokiame stulpelyje.

IN moderni forma Sudoku galvosūkiai pirmą kartą buvo paskelbti 1979 m. žurnale Word Games. Dėlionės autorius buvo Harvardas Harrisas iš Indianos. Dėlionė „Skaičiaus vieta“ (išvertus į rusų kalbą – „numerio vieta“) – tai gali būti laikoma vienu iš pirmųjų šiuolaikinio Sudoku leidimų. Pridėjo 3x3 langelių blokus, o tai buvo svarbus patobulinimas, nes leido dėlionę padaryti įdomesnę. Jis panaudojo Eulerio lotyniško kvadrato principą, pritaikė jį 9x9 matricoje ir pridėjo papildomų apribojimų, skaičiai neturėtų kartotis vidiniuose 3x3 kvadratuose.

Taigi, kaip daugelis galvoja, Sudoku idėja kilo ne iš Japonijos, tačiau žaidimo pavadinimas tikrai japoniškas.

Japonijoje šį galvosūkį 1984 m. balandžio mėn. žurnale „Monthly Nicolist“ paskelbė Nicoly Inc., pagrindinė įvairių galvosūkių rinkinių leidėja, pavadinimu „Skaičius gali būti naudojamas tik vieną kartą“. 2004 m. lapkričio 12 d. „The Times“ savo puslapiuose paskelbė pirmąjį „Sudoku“ galvosūkį. Šis leidinys tapo sensacija, galvosūkis greitai išplito visoje Britanijoje, Australijoje, Naujojoje Zelandijoje; išpopuliarėjo JAV.

Sudoku variantai

Taigi, kas yra Sudoku? Šiuo metu yra daug šio populiaraus galvosūkio tipo atnaujinimų, tačiau klasikinis Sudoku yra 9x9 kvadratas, padalintas į kvadratus, kurių kiekvienoje kraštinės yra po 3 langelius. Taigi bendras žaidimo laukas yra 81 langelis. Darbo priede įdėsiu skirtingi tipai Sudoku ir galimi sprendimai (mano tėvai padėjo juos išspręsti).

Sudoku sudėtingumo lygis skiriasi priklausomai nuo kvadrato dydžio:

• 1. Mažiesiems galvosūkių mėgėjams Sudoku gaminamas su 2x2, 6x6 langelių laukeliais.
• 2. Profesionalams yra Sudoku 15x15 ir 16x16 langeliai

Yra sudoku skirtingi lygiai:

• lengva
• vidurio
• sunku
• labai sudėtinga
• super kompleksas

Sprendimo taisyklės

Sudoku galvosūkiai turi tik vieną taisyklę. Būtina užpildyti laisvus langelius, kad kiekvienoje eilutėje, kiekviename stulpelyje ir kiekviename mažame 3X3 kvadrate kiekvienas skaičius nuo 1 iki 9 atsirastų tik 1 kartą. Kai kurios Sudoku langeliai jau užpildyti skaičiais, o likusias belieka užpildyti jums. Kuo daugiau skaičių iš pradžių, tuo lengviau išspręsti galvosūkį. Beje, teisingai sudarytas Sudoku turi tik vieną sprendimą.

Sudoku sprendimas

Sudoku sprendimo strategija apima tris veiksmus:

• išmokti dėlionėje esančių skaičių vietą
• preliminarus skaičių išdėstymas
• analizė

Geriausias būdas sprendimai – kairiojo langelio kampo viršuje parašykite kandidatų numerius. Po to galite tiksliai pamatyti skaičius, kurie turėtų užimti šią langelį. Sudoku reikia žaisti lėtai, nes tai atpalaiduojantis žaidimas. Kai kurie galvosūkiai gali būti išspręsti per kelias minutes, tačiau kiti gali užtrukti valandas, o kai kuriais atvejais net dienas.

Matematinis pagrindas. Pagal Berthamo Felgenhauerio skaičiavimus, 9x9 Sudoku galimų kombinacijų skaičius yra 6 670 903 752 021 072 936 960.

Kuris padės jums vystytis vienam iš svarbiausių organų – smegenų. Žinoma, vienas iš jų yra gerai žinomi japoniški sudoku galvosūkiai. Su jų pagalba galite beveik „papūsti smegenis“, nes be to, kad reikia apskaičiuoti daugybę skaičių išdėstymo variantų, jūs taip pat turite sugebėti tai padaryti porą dešimčių judesių į priekį. Žodžiu, čia tikras rojus, jei nori, kad neuronai neišsausėtų. O šiandien apžvelgsime pagrindinius Sudoku ekspertų naudojamus triukus. Tai bus naudinga tiek pradedantiesiems, tiek seniems šių galvosūkių gerbėjams. Juk kažkas turi žengti pirmuosius žingsnius sudoku mene, o kažkas turi pagerinti savo sprendimų efektyvumą!

taisykles

Jei dar nesate susipažinę, pirmiausia turėtumėte susipažinti su taisyklėmis. Patikėkite, jie labai paprasti.

Žaidimo laukas yra kvadratas, kurio matmenys yra 9 × 9. Tuo pačiu metu jis yra padalintas į mažesnius kvadratus, kurių matmenys yra 3 × 3. Tai yra, visas laukas susideda iš 81 langelio.

Problemos sąlyga yra skaičiai, kurie jau yra šiose ląstelėse.

Blokas (ląstelių blokas) – mažas kvadratas, linija arba linija.

Ką reikia padaryti: sutvarkykite visus kitus numerius laikydamiesi kelių taisyklių. Pirma, kiekviename mažame kvadrate neturėtų būti pasikartojimų. Antra, visuose stulpeliuose ir eilutėse taip pat neturėtų būti pasikartojimų. Tai reiškia, kad kiekviename iš šių blokų kiekvienas skaičius turi būti tik vieną kartą. Kad viskas būtų dar aiškiau, atkreipkite dėmesį į išspręstą Sudoku:

Bazinis sprendimas

Paprastai, jei sprendžiate paprastą „Sudoku“, tereikia surašyti visas galimas parinktis kiekvienai iš 81 langelio ir palaipsniui išbraukti netinkamas parinktis. Tai labai paprasta.

Bet jei pakilsite į aukštesnį lygį, iki sudėtingesnio Sudoku, viskas taps įdomiau. Dažnai atsitiks taip, kad nėra galimybės dėti naujų skaičių ir turėsite pereiti prie prielaidų: „Tebūnie toks skaičius“, po kurio turėsite apsvarstyti šią hipotezę ir arba rasti problemos sprendimą. problema arba jūsų prielaidos prieštaravimas.

Tačiau, žinoma, yra specialių gudrybių, kurios padės visa tai atlikti efektyviau.

gudrybės

1. Nuogos poros/trejetai/ketvertai

Jei viename bloke (kvadrate, eilutėje ar stulpelyje) yra du langeliai, kuriuose galite dėti tik 2 skaičius, tuomet akivaizdu, kad šiuos skaičius galima pašalinti iš kitų šio bloko langelių galimų parinkčių.

Be to, šį triuką galima nesunkiai atlikti su trigubais ir keturiais:

2. Paslėptos poros

Labai naudinga technika, tam tikra prasme, priešinga nuogoms poroms. Jei kai kuriose dviejose vieno kvadrato langeliuose „ galimybės Jūs turite skaičius, kurie niekur kitur nesikartoja (šiame kvadrate), tada visi kiti skaičiai iš šių dviejų langelių gali būti pašalinti.

Kad būtų dar aiškiau, atkreipkite dėmesį į pavyzdžius (vieną paprastą ir sudėtingesnį):

Laimei, tai veikia ir trigubai, ir ketvertui, tačiau verta paminėti labai svarbų ir labai šaunų triuką. Nebūtina, kad trijose/keturiose langeliuose būtų tie patys 3 formos (a;b;c) (a;b;c) (a;b;c) skaitmenys. Jums pakaks šios parinkties: (a;b) (b;c) (a;c).

3. Bevardė taisyklė

Jei viename stulpelyje / eilutėje turite porą ar trigubą, kurie yra tame pačiame kvadrate, galite saugiai pašalinti šiuos skaičius iš kitų šio kvadrato langelių.

4. Rodyklės poros

Jei vienoje eilutėje / stulpelyje „parinktys“ yra dvi parinktys tie patys skaitmenys, tada tokius skaičius galima pašalinti iš atitinkamo stulpelio/eilutės.

Kartais tai gali būti labai naudinga, ypač jei randate kelias iš šių porų:

Žinoma, šiuo atveju šių skaičių kitose kvadrato ląstelėse neturėtų būti, tačiau pagal neįvardytą taisyklę to nereikia.

Mėgstate sudoku ir kitas mįsles, žaidimus, galvosūkius ir testus, skirtus įvairiems mąstymo aspektams lavinti? Gaukite prieigą prie visos interaktyvios medžiagos svetainėje, kad galėtumėte efektyviau kurti.

Išvada

Apžvelgėme pagrindinius metodus, kurie naudojami sprendžiant Sudoku. Atkreipiu dėmesį, kad tai tik pradžia, o kituose straipsniuose apžvelgsime sudėtingesnius ir įdomesnius lustus, kurių dėka tokių problemų sprendimas taps dar įdomesnis ir paprastesnis.

Kaip mokymas, 4brain leidimas kviečia susipažinti su failu, kuriame yra sudoku skirtingi lygiai sunkumų. Skirkite laiko praktikai, nes jei šiai pamokai skirsite pakankamai laiko, šio straipsnių kurso pabaigoje, patikėkite, tapsite tikru asu spręsdami japoniškus galvosūkius.

Jei turite klausimų apie šiuos metodus ar Sudoku, kuriuos pridedame prie straipsnio, nedvejodami užduokite juos komentaruose!