Trigonometrikus táblázat. Szinusz, koszinusz, érintő és kotangens - minden, amit tudnia kell az egységes matematika államvizsgáról

Egy ponton középre állítva A.
α - radiánban kifejezett szög.

Meghatározás
Szinusz (sin α) egy trigonometrikus függvény, amely egy derékszögű háromszög befogója és szára közötti α szögtől függ, egyenlő a szemközti szár hosszának arányával |BC| a hypotenus hosszára |AC|.

Koszinusz (cos α) egy trigonometrikus függvény, amely egy derékszögű háromszög befogója és szára közötti α szögtől függ, egyenlő a szomszédos szár hosszának arányával |AB| a hypotenus hosszára |AC|.

Elfogadott jelölések

;
;
.

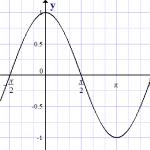
A szinuszfüggvény grafikonja, y = sin x

A koszinusz függvény grafikonja, y = cos x

A szinusz és a koszinusz tulajdonságai

Periodikaság

Függvények y = bűn xés y = cos x periodikus periódussal 2π.

Paritás

A szinuszfüggvény páratlan. A koszinusz függvény páros.

Definíció és értékek tartománya, szélsőség, növekedés, csökkenés

A szinusz és koszinusz függvények definíciós tartományukban folytonosak, azaz minden x-re (lásd a folytonosság bizonyítását). Főbb tulajdonságaikat a táblázat mutatja be (n - egész).

	y = bűn x	y = cos x
Hatály és folytonosság	- ∞ < x < + ∞	- ∞ < x < + ∞
Értékek tartománya	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Növekvő
Csökkenő
Maxima, y = 1
Minimum, y = - 1
Nullák, y = 0
Metszéspontok az ordináta tengellyel, x = 0	y = 0	y = 1

Alapképletek

A szinusz és a koszinusz négyzetösszege

Szinusz és koszinusz képlete összegből és különbségből

;
;

Képletek szinuszok és koszinuszok szorzatára

Összeg és különbség képletek

Szinusz kifejezése koszinuszon keresztül

;
;
;
.

Koszinusz kifejezése szinuszon keresztül

;
;
;
.

Kifejezés érintőn keresztül

; .

Mikor van nálunk:
; .

Nál nél :
; .

Szinuszok és koszinuszok, érintők és kotangensek táblázata

Ez a táblázat a szinuszok és koszinuszok értékeit mutatja az argumentum bizonyos értékeihez.

Kifejezések összetett változókon keresztül

;

Euler-képlet

Kifejezések hiperbolikus függvényeken keresztül

;
;

Származékok

; . Képletek származtatása >>>

N-edrendű származékai:
{ -∞ < x < +∞ }

Szekáns, koszekáns

Inverz függvények

A szinusz és a koszinusz inverz függvénye arszinusz, illetve arkoszinusz.

Arcsine, arcsin

Arccosine, arccos

Referenciák:
BAN BEN. Bronstein, K.A. Semendyaev, Matematika kézikönyve mérnökök és főiskolai hallgatók számára, „Lan”, 2009.

Ez a cikk tartalmazza szinuszok, koszinuszok, érintők és kotangensek táblázatai. Először megadjuk a trigonometrikus függvények alapértékeinek táblázatát, azaz a 0, 30, 45, 60, 90, ..., 360 fokos szögek szinuszainak, koszinuszainak, érintőinek és kotangenseinek táblázatát ( 0, π/6, π/4, π/3, π/2, …, 2π radián). Ezt követően adunk egy táblázatot a szinuszokról és koszinuszokról, valamint V. M. Bradis érintők és kotangensek táblázatáról, és megmutatjuk, hogyan kell ezeket a táblázatokat használni a trigonometrikus függvények értékeinek megtalálásához.

Oldalnavigáció.

Szinuszok, koszinuszok, érintők és kotangensek táblázata 0, 30, 45, 60, 90, ... fokos szögekhez

Bibliográfia.

Algebra: Tankönyv 9. osztály számára. átl. iskola/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Szerk. S. A. Telyakovsky. - M.: Oktatás, 1990. - 272 pp.: ill. - ISBN 5-09-002727-7
Basmakov M. I. Az algebra és az elemzés kezdetei: Tankönyv. 10-11 évfolyamnak. átl. iskola - 3. kiadás - M.: Nevelés, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
Algebraés az elemzés kezdete: Proc. 10-11 évfolyamnak. Általános oktatás intézmények / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn és mások; Szerk. A. N. Kolmogorov - 14. kiadás - M.: Oktatás, 2004. - 384 old.: ill. - ISBN 5-09-013651-3.
Gusev V. A., Mordkovich A. G. Matematika (kézikönyv a műszaki iskolákba jelentkezők számára): Proc. pótlék.- M.; Magasabb iskola, 1984.-351 p., ill.
Bradis V. M. Négyjegyű matematikai táblázatok: Általános oktatáshoz. tankönyv létesítmények. - 2. kiadás - M.: Túzok, 1999.- 96 p.: ill. ISBN 5-7107-2667-2

A trigonometria tanulmányozását a derékszögű háromszöggel kezdjük. Határozzuk meg, mi a szinusz és a koszinusz, valamint egy hegyesszög érintője és kotangense. Ez a trigonometria alapjai.

Hadd emlékeztessük erre derékszög egy 90 fokkal egyenlő szög. Más szóval, fél elfordított szög.

Éles sarok- kevesebb, mint 90 fok.

Tompaszög- 90 foknál nagyobb. Egy ilyen szöghöz képest a „tompa” nem sértés, hanem matematikai kifejezés :-)

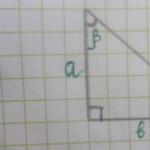
Rajzoljunk egy derékszögű háromszöget. A derékszöget általában jelöli. Felhívjuk figyelmét, hogy a sarokkal szemközti oldalt ugyanaz a betű jelzi, csak kicsi. Így az A szemközti szöget jelöljük.

A szöget a megfelelő görög betűvel jelöljük.

Átfogó derékszögű háromszögnek a derékszöggel ellentétes oldala.

Lábak- hegyesszögekkel ellentétes oldalak.

A szöggel szemben fekvő lábat ún szemben(szöghez viszonyítva). A másik láb, amely a szög egyik oldalán fekszik, ún szomszédos.

Sinus A derékszögű háromszög hegyesszöge a szemközti oldal és a hipotenusz aránya:

Koszinusz hegyesszög egy derékszögű háromszögben - a szomszédos láb és a hipotenusz aránya:

Tangens hegyesszög egy derékszögű háromszögben - az ellenkező oldal és a szomszédos oldal aránya:

Egy másik (ekvivalens) definíció: egy hegyesszög érintője a szög szinuszának és koszinuszának aránya:

Kotangens hegyesszög egy derékszögű háromszögben - a szomszédos oldal és az ellenkező oldal aránya (vagy, ami megegyezik, a koszinusz és a szinusz aránya):

Jegyezze meg az alábbiakban a szinusz, koszinusz, érintő és kotangens alapvető összefüggéseit. Hasznosak lesznek a problémák megoldása során.

Bizonyítsunk be néhányat közülük.

Oké, megadtuk a definíciókat és felírtuk a képleteket. De miért van szükségünk még mindig szinuszra, koszinuszra, érintőre és kotangensre?

Tudjuk bármely háromszög szögeinek összege egyenlő.

Ismerjük a közti kapcsolatot a felek derékszögű háromszög. Ez a Pitagorasz-tétel: .

Kiderült, hogy egy háromszög két szögének ismeretében megtalálhatja a harmadikat. Egy derékszögű háromszög két oldalának ismeretében megtalálhatja a harmadikat. Ez azt jelenti, hogy a szögeknek megvan a saját arányuk, és az oldalaknak megvan a sajátjuk. De mit kell tennie, ha egy derékszögű háromszögben ismeri az egyik szöget (kivéve a derékszöget) és az egyik oldalt, de meg kell találnia a többi oldalt?

Ezzel találkoztak az emberek a múltban, amikor térképeket készítettek a területről és a csillagos égboltról. Végül is nem mindig lehet közvetlenül megmérni a háromszög minden oldalát.

Szinusz, koszinusz és érintő – más néven trigonometrikus szögfüggvények- közötti kapcsolatokat adni a felekÉs sarkok háromszög. A szög ismeretében speciális táblázatok segítségével megtalálhatja az összes trigonometrikus függvényét. És a háromszög és az egyik oldal szögeinek szinuszainak, koszinuszainak és érintőinek ismeretében megtalálhatja a többit.

Rajzolunk egy táblázatot is a szinusz, koszinusz, tangens és kotangens értékeiről a „jó” szögekhez tól-ig.

Kérjük, vegye figyelembe a két piros kötőjelet a táblázatban. Megfelelő szögértékeknél az érintő és a kotangens nem létezik.

Nézzünk meg néhány trigonometriai problémát a FIPI Feladatbankból.

1. Egy háromszögben a szög , . Megtalálja .

A probléma négy másodperc alatt megoldódik.

Mert a , .

2. Egy háromszögben a szög , , . Megtalálja .

Keressük meg a Pitagorasz-tétel segítségével.

A probléma megoldódott.

A problémákban gyakran vannak háromszögek szögekkel és vagy szögekkel és. Emlékezz fejből az alapvető arányokra!

Egy olyan háromszögnél, amelynek szögei és az at szöggel ellentétes szár egyenlő a hypotenus fele.

Egy háromszög szögekkel és egyenlő szárú. Ebben a hypotenusa szor nagyobb, mint a láb.

Megvizsgáltuk a derékszögű háromszögek megoldásának problémáit – vagyis az ismeretlen oldalak vagy szögek megtalálását. De ez még nem minden! A matematika egységes államvizsgán sok olyan feladat van, ahol egy háromszög külső szögének szinusza, koszinusza, érintője vagy kotangense. Erről bővebben a következő cikkben.

TRIGONOMETRIAI FUNKCIÓK ÉRTÉKTÁBLÁZATA

A trigonometrikus függvények értéktáblázata a 0, 30, 45, 60, 90, 180, 270 és 360 fokos szögekre és a megfelelő szögértékekre van összeállítva vradiánban. A trigonometrikus függvények közül a táblázatban a szinusz, koszinusz, érintő, kotangens, szekáns és koszekáns látható. Az iskolai példák megoldásának kényelme érdekében a trigonometrikus függvények értékeit a táblázatban tört alakban írják, miközben megőrzik a számok négyzetgyökének kinyerésére szolgáló jeleket, ami nagyon gyakran segít csökkenteni a bonyolult matematikai kifejezéseket. Érintő és kotangens esetén egyes szögek értéke nem határozható meg. Az ilyen szögek érintőjének és kotangensének értékéhez kötőjel van a trigonometrikus függvények értéktáblázatában. Általánosan elfogadott, hogy az ilyen szögek érintője és kotangense egyenlő a végtelennel. Külön oldalon találhatók a trigonometrikus függvények csökkentésére szolgáló képletek.

A trigonometrikus szinuszfüggvény értéktáblázata a következő szögek értékeit mutatja: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 fokban, ami megfelel sin 0 pi, sin pi/6, sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi radián szögmértékben. Iskolai szinusztáblázat.

A trigonometrikus koszinuszfüggvényhez a táblázat a következő szögek értékeit mutatja: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 fokban, ami cos 0 pi-nek felel meg. , cos pi 6, cos pi 4, cos pi 3, cos pi 2, cos pi, cos 3 pi 2, cos 2 pi radián szögmértékben. Iskolai koszinusz táblázat.

A trigonometrikus érintőfüggvény trigonometrikus táblázata a következő szögekhez ad értékeket: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 fokban, ami tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi a szögek radián mértékében. A trigonometrikus érintőfüggvények következő értékei nincsenek definiálva tan 90, tan 270, tan pi/2, tan 3 pi/2, és egyenlőnek tekintendők a végtelennel.

A trigonometrikus függvény kotangenséhez a trigonometrikus táblázatban a következő szögek értékei vannak megadva: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 fokban, ami megfelel ctg pi/6, ctg pi/4 , ctg pi/3, tg pi/ 2, tan 3 pi/2 radián szögmértékben. A trigonometrikus kotangens függvények alábbi értékei nincsenek definiálva ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi, és egyenlőnek tekintendők a végtelennel.

A szekáns és koszekáns trigonometrikus függvények értékei ugyanazokra a szögekre vannak megadva fokban és radiánban, mint a szinusz, koszinusz, érintő, kotangens.

A nem szabványos szögek trigonometrikus függvényeinek táblázata a szinusz, koszinusz, tangens és kotangens értékeit mutatja szögeknél 15, 18, 22,5, 36, 54, 67,5 72 fokban és radiánban pi/12 , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radián. A trigonometrikus függvények értékeit törtekben és négyzetgyökökben fejezzük ki, hogy megkönnyítsük a törtek csökkentését az iskolai példákban.

Még három trigonometrikus szörny. Az első az 1,5 másfél fok vagy a pi érintője osztva 120-zal. A második a pi koszinusza osztva 240-nel, pi/240. A leghosszabb a pi koszinusza osztva 17-tel, pi/17.

A szinusz és koszinusz függvények trigonometrikus értékköre vizuálisan ábrázolja a szinusz és a koszinusz előjeleit a szög nagyságától függően. Különösen a szőkék esetében a koszinusz értékek zöld vonallal vannak aláhúzva, hogy csökkentsék a zavartságot. A fokok radiánra váltása is nagyon világosan látható, ha a radiánokat pi-ben fejezzük ki.

Ez a trigonometrikus táblázat a szinusz, a koszinusz, az érintő és a kotangens értékeit mutatja be 0 nulla és 90 kilencven fok közötti szögek esetén, egyfokos időközönként. Az első negyvenöt foknál a trigonometrikus függvények neveit a táblázat tetején kell nézni. Az első oszlop fokokat tartalmaz, a következő négy oszlopba a szinuszok, koszinuszok, érintők és kotangensek értékeit írjuk.

A negyvenöt foktól kilencven fokig terjedő szögeknél a trigonometrikus függvények neveit a táblázat aljára írjuk. Az utolsó oszlop a fokokat tartalmazza, a koszinuszok, szinuszok, kotangensek és érintők értékeit az előző négy oszlopba írjuk. Legyen óvatos, mert a trigonometrikus függvények nevei a trigonometrikus táblázat alján eltérnek a táblázat tetején található nevektől. A szinuszok és koszinuszok felcserélődnek, csakúgy, mint az érintő és a kotangens. Ez a trigonometrikus függvények értékeinek szimmetriájának köszönhető.

A trigonometrikus függvények előjeleit a fenti ábra mutatja. A szinusz pozitív értékei 0 és 180 fok között, vagy 0 és pi között vannak. A szinusz negatív értékei 180 és 360 fok között, vagy pi és 2 pi között vannak. A koszinusz értékek pozitívak 0 és 90 és 270 és 360 fok között, vagy 0 és 1/2 pi és 3/2 és 2 pi között. Az érintő és a kotangens pozitív értéke 0 és 90 fok között, valamint 180 és 270 fok között van, ami a 0 és 1/2 pi és a pi és 3/2 pi közötti értékeknek felel meg. Az érintő és a kotangens negatív értékei 90-180 fok és 270-360 fok, vagy 1/2 pi-től pi-ig és 3/2 pi-től 2 pi-ig. A trigonometrikus függvények előjeleinek meghatározásakor 360 foknál vagy 2 pi-nél nagyobb szögeknél ezeknek a függvényeknek a periodicitási tulajdonságait kell használni.

A szinusz, az érintő és a kotangens trigonometrikus függvények páratlan függvények. Ezeknek a függvényeknek a negatív szögek értéke negatív lesz. A koszinusz egy egyenletes trigonometrikus függvény - a negatív szög koszinusz értéke pozitív lesz. A trigonometrikus függvények szorzásakor és osztásakor előjelszabályokat kell követni.

A trigonometrikus szinuszfüggvény értéktáblázata a következő szögek értékeit mutatja
Dokumentum
A redukciós képletek külön oldalon találhatók trigonometrikusfunkciókat. BAN BEN asztalértékeketMerttrigonometrikusfunkciókatsinusadottértékeketMerta következősarkok: bűn 0, bűn 30, bűn 45 ...
A javasolt matematikai berendezés az n-dimenziós hiperkomplex számok komplex számításának teljes analógja tetszőleges számú n szabadságfokkal, és nemlineárisok matematikai modellezésére szolgál.
Dokumentum
... funkciókat egyenlő funkciókat Képek. Ebből a tételből kellene, Mit Mert megtalálva az U, V koordinátákat, elég kiszámolni funkció... geometria; polynar funkciókat(a kétdimenziós többdimenziós analógjai trigonometrikusfunkciókat), tulajdonságaik, táblázatokés alkalmazás; ...
Azt is ajánljuk