Find the angle between direct given equations. Angle between lines

Definition. If two lines are given y = k 1 x + b 1 , y = k 2 x + b 2 , then the acute angle between these lines will be defined as

Two lines are parallel if k 1 = k 2 . Two lines are perpendicular if k 1 = -1/ k 2 .

Theorem. The straight lines Ax + Vy + C \u003d 0 and A 1 x + B 1 y + C 1 \u003d 0 are parallel when the coefficients A 1 \u003d λA, B 1 \u003d λB are proportional. If also С 1 = λС, then the lines coincide. The coordinates of the point of intersection of two lines are found as a solution to the system of equations of these lines.

Equation of a line passing through a given point

Perpendicular to this line

Definition. The line passing through the point M 1 (x 1, y 1) and perpendicular to the line y \u003d kx + b is represented by the equation:

Distance from point to line

Theorem. If a point M(x 0, y 0) is given, then the distance to the line Ax + Vy + C \u003d 0 is defined as

.

Proof. Let the point M 1 (x 1, y 1) be the base of the perpendicular dropped from the point M to the given line. Then the distance between points M and M 1:

(1)

The x 1 and y 1 coordinates can be found as a solution to the system of equations:

The second equation of the system is the equation of a straight line passing through a given point M 0 perpendicular to a given straight line. If we transform the first equation of the system to the form:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

then, solving, we get:

Substituting these expressions into equation (1), we find:

The theorem has been proven.

Example. Determine the angle between the lines: y = -3 x + 7; y = 2 x + 1.

k 1 \u003d -3; k2 = 2; tgφ = ; φ= p /4.

Example. Show that the lines 3x - 5y + 7 = 0 and 10x + 6y - 3 = 0 are perpendicular.

Solution. We find: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, therefore, the lines are perpendicular.

Example. The vertices of the triangle A(0; 1), B (6; 5), C (12; -1) are given. Find the equation for the height drawn from vertex C.

Solution. We find the equation of the side AB: ; 4 x = 6 y - 6;

2x – 3y + 3 = 0;

The desired height equation is: Ax + By + C = 0 or y = kx + b. k = . Then y = . Because height passes through point C, then its coordinates satisfy this equation: whence b = 17. Total: .

Answer: 3x + 2y - 34 = 0.

Equation of a line passing through a given point in a given direction. Equation of a straight line passing through two given points. Angle between two lines. Condition of parallelism and perpendicularity of two lines. Determining the point of intersection of two lines

1. Equation of a line passing through a given point A(x 1 , y 1) in a given direction, determined by the slope k,

y - y 1 = k(x - x 1). (1)

This equation defines a pencil of lines passing through a point A(x 1 , y 1), which is called the center of the beam.

2. Equation of a straight line passing through two points: A(x 1 , y 1) and B(x 2 , y 2) is written like this:

The slope of a straight line passing through two given points is determined by the formula

3. Angle between straight lines A And B is the angle by which the first straight line must be rotated A around the point of intersection of these lines counterclockwise until it coincides with the second line B. If two lines are given by slope equations

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

then the angle between them is determined by the formula

It should be noted that in the numerator of the fraction, the slope of the first straight line is subtracted from the slope of the second straight line.

If the equations of a straight line are given in general view

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

the angle between them is determined by the formula

4. Conditions for parallelism of two lines:

a) If the lines are given by equations (4) with a slope, then the necessary and sufficient condition for their parallelism is the equality of their slopes:

k 1 = k 2 . (8)

b) For the case when the lines are given by equations in general form (6), the necessary and sufficient condition for their parallelism is that the coefficients at the corresponding current coordinates in their equations are proportional, i.e.

5. Conditions for perpendicularity of two lines:

a) In the case when the lines are given by equations (4) with a slope, the necessary and sufficient condition for their perpendicularity is that they slope factors are reciprocal in magnitude and opposite in sign, i.e.

This condition can also be written in the form

k 1 k 2 = -1. (11)

b) If the equations of straight lines are given in general form (6), then the condition for their perpendicularity (necessary and sufficient) is to fulfill the equality

A 1 A 2 + B 1 B 2 = 0. (12)

6. The coordinates of the point of intersection of two lines are found by solving the system of equations (6). Lines (6) intersect if and only if

1. Write the equations of the lines passing through the point M, one of which is parallel and the other is perpendicular to the given line l.

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get

The conditions of parallelism and perpendicularity of two lines are equivalent to the conditions of parallelism and perpendicularity of their direction vectors and:

Two straight are parallel if and only if their respective coefficients are proportional, i.e. l 1 parallel l 2 if and only if parallel .

Two straight perpendicular if and only if the sum of the products of the corresponding coefficients is equal to zero: .

At goal between line and plane

Let the line d- not perpendicular to the plane θ;
d′− projection of a straight line d to the plane θ;
The smallest of the angles between straight lines d And d′ we will call angle between line and plane.
Let's denote it as φ=( d,θ)
If d⊥θ , then ( d,θ)=π/2

Oi→j→k→− rectangular coordinate system.
Plane equation:

θ: Ax+By+cz+D=0

We consider that the line is given by a point and a direction vector: d[M 0,p→]
Vector n→(A,B,C)⊥θ
Then it remains to find out the angle between the vectors n→ and p→, denote it as γ=( n→,p→).

If the angle γ<π/2 , то искомый угол φ=π/2−γ .

If the angle γ>π/2 , then the required angle φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Then, angle between line and plane can be calculated using the formula:

sinφ=∣cosγ∣=∣ ∣ Ap 1+bp 2+cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23

Question 29. The concept of a quadratic form. The sign-definiteness of quadratic forms.

Quadratic form j (x 1, x 2, ..., x n) n real variables x 1, x 2, ..., x n is called a sum of the form
, (1)

where aij are some numbers called coefficients. Without loss of generality, we can assume that aij = a ji.

The quadratic form is called valid, if aij О GR. Matrix of quadratic form is called the matrix composed of its coefficients. Quadratic form (1) corresponds to a unique symmetric matrix
i.e. A T = A. Therefore, quadratic form (1) can be written in matrix form j ( X) = x T Ah, where x T = (X 1 X 2 … x n). (2)

And vice versa, any symmetric matrix (2) corresponds to a unique quadratic form up to the notation of variables.

The rank of the quadratic form is called the rank of its matrix. The quadratic form is called non-degenerate, if its matrix is ​​nonsingular BUT. (recall that the matrix BUT is called non-degenerate if its determinant is not zero). Otherwise, the quadratic form is degenerate.

positive definite(or strictly positive) if

j ( X) > 0 , for anyone X = (X 1 , X 2 , …, x n), except X = (0, 0, …, 0).

The matrix BUT positive definite quadratic form j ( X) is also called positive definite. Therefore, a positive definite quadratic form corresponds to a unique positive definite matrix and vice versa.

The quadratic form (1) is called negative definite(or strictly negative) if

j ( X) < 0, для любого X = (X 1 , X 2 , …, x n), except X = (0, 0, …, 0).

Similarly as above, a negative-definite quadratic matrix is ​​also called negative-definite.

Therefore, a positively (negatively) definite quadratic form j ( X) reaches the minimum (maximum) value j ( X*) = 0 for X* = (0, 0, …, 0).

Note that most of the quadratic forms are not sign-definite, that is, they are neither positive nor negative. Such quadratic forms vanish not only at the origin of the coordinate system, but also at other points.

When n> 2, special criteria are required to check the sign-definiteness of a quadratic form. Let's consider them.

Major Minors quadratic form are called minors:

that is, these are minors of order 1, 2, …, n matrices BUT located in the left upper corner, the last of them coincides with the determinant of the matrix BUT.

Criterion for positive definiteness (Sylvester criterion)

X) = x T Ah is positive definite, it is necessary and sufficient that all principal minors of the matrix BUT were positive, that is: M 1 > 0, M 2 > 0, …, M n > 0. Criterion of negative certainty In order for the quadratic form j ( X) = x T Ah is negative definite, it is necessary and sufficient that its principal minors of even order be positive, and those of odd order are negative, i.e.: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

ANGLE BETWEEN PLANES

Let's consider two planes α 1 and α 2 given respectively by the equations:

Under corner between two planes we will understand one of dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . That's why . Because And , then

.

Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, and hence .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

In this way, .

Examples.

DIRECT IN SPACE.

VECTOR EQUATION DIRECT.

PARAMETRIC EQUATIONS DIRECT

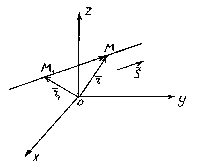
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding the vector of this line.

So let the straight l passes through a point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. It can be seen from the figure that .

The vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t is called a parameter. Denoting the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector straight line equation. It shows that each parameter value t corresponds to the radius vector of some point M lying on a straight line.

We write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric straight line equations.

When changing the parameter t coordinates change x, y And z and dot M moves in a straight line.

CANONICAL EQUATIONS DIRECT

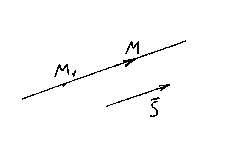
Let be M 1 (x 1 , y 1 , z 1) - a point lying on a straight line l, And is its direction vector. Again, take an arbitrary point on a straight line M(x,y,z) and consider the vector .

It is clear that the vectors and are collinear, so their respective coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the line could be obtained from the parametric equations by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in a parametric way.

Denote , hence x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the line be perpendicular to one of the coordinate axes, for example, the axis Ox. Then the direction vector of the line is perpendicular Ox, Consequently, m=0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

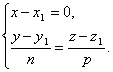
However, in this case too, we agree to formally write the canonical equations of the straight line in the form . Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox And Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS A DIRECT LINE AS A LINE OF INTERCEPTION OF TWO PLANES

Through each straight line in space passes an infinite number of planes. Any two of them, intersecting, define it in space. Therefore, the equations of any two such planes, considered together, are the equations of this line.

In general, any two non-parallel planes given by the general equations

determine their line of intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

To construct a line, it is enough to find any two of its points. The easiest way is to choose the points of intersection of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of a straight line, assuming z= 0:

Solving this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line, one can proceed to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors And . Therefore, for the direction vector of the straight line l you can take the cross product of normal vectors:

.

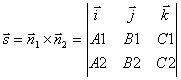Example. Give the general equations of the straight line to the canonical form.

Find a point on a straight line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

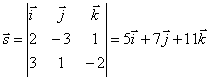. Consequently, l: .

ANGLE BETWEEN RIGHTS

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get

I will be brief. The angle between two lines is equal to the angle between their direction vectors. Thus, if you manage to find the coordinates of the direction vectors a \u003d (x 1; y 1; z 1) and b \u003d (x 2; y 2; z 2), you can find the angle. More precisely, the cosine of the angle according to the formula:

Let's see how this formula works on specific examples:

A task. Points E and F are marked in the cube ABCDA 1 B 1 C 1 D 1 - the midpoints of the edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AE and BF.

Since the edge of the cube is not specified, we set AB = 1. We introduce a standard coordinate system: the origin is at point A, and the x, y, z axes are directed along AB, AD, and AA 1, respectively. The unit segment is equal to AB = 1. Now let's find the coordinates of the direction vectors for our lines.

Find the coordinates of the vector AE. To do this, we need points A = (0; 0; 0) and E = (0.5; 0; 1). Since the point E is the middle of the segment A 1 B 1 , its coordinates are equal to the arithmetic mean of the coordinates of the ends. Note that the origin of the vector AE coincides with the origin, so AE = (0.5; 0; 1).

Now let's deal with the BF vector. Similarly, we analyze the points B = (1; 0; 0) and F = (1; 0.5; 1), because F - the middle of the segment B 1 C 1 . We have:
BF = (1 - 1; 0.5 - 0; 1 - 0) = (0; 0.5; 1).

So, the direction vectors are ready. The cosine of the angle between the lines is the cosine of the angle between the direction vectors, so we have:

A task. In a regular trihedral prism ABCA 1 B 1 C 1 , all edges of which are equal to 1, points D and E are marked - the midpoints of the edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AD and BE.

We introduce a standard coordinate system: the origin is at point A, the x-axis is directed along AB, z - along AA 1 . We direct the y axis so that the OXY plane coincides with the ABC plane. The unit segment is equal to AB = 1. Find the coordinates of the direction vectors for the desired lines.

First, let's find the coordinates of the AD vector. Consider the points: A = (0; 0; 0) and D = (0.5; 0; 1), because D - the middle of the segment A 1 B 1 . Since the beginning of the vector AD coincides with the origin, we get AD = (0.5; 0; 1).

Now let's find the coordinates of the vector BE. Point B = (1; 0; 0) is easy to calculate. With point E - the middle of the segment C 1 B 1 - a little more complicated. We have:

It remains to find the cosine of the angle:

A task. In a regular hexagonal prism ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , all edges of which are equal to 1, the points K and L are marked - the midpoints of the edges A 1 B 1 and B 1 C 1, respectively. Find the angle between lines AK and BL.

We introduce a standard coordinate system for a prism: we place the origin of coordinates at the center of the lower base, direct the x-axis along FC, the y-axis through the midpoints of segments AB and DE, and the z-axis vertically upwards. The unit segment is again equal to AB = 1. Let us write out the coordinates of the points of interest to us:

Points K and L are the midpoints of the segments A 1 B 1 and B 1 C 1, respectively, so their coordinates are found through the arithmetic mean. Knowing the points, we find the coordinates of the direction vectors AK and BL:

Now let's find the cosine of the angle:

A task. In the right quadrangular pyramid SABCD, all edges of which are equal to 1, points E and F are marked - the midpoints of the sides SB and SC, respectively. Find the angle between lines AE and BF.

We introduce a standard coordinate system: the origin is at point A, the x and y axes are directed along AB and AD, respectively, and the z axis is directed vertically upwards. The unit segment is equal to AB = 1.

Points E and F are the midpoints of the segments SB and SC, respectively, so their coordinates are found as the arithmetic mean of the ends. We write down the coordinates of the points of interest to us:
A = (0; 0; 0); B = (1; 0; 0)

Knowing the points, we find the coordinates of the direction vectors AE and BF:

The coordinates of the vector AE coincide with the coordinates of point E, since point A is the origin. It remains to find the cosine of the angle: