Quadratic equations are not equal to zero. Quadratic equations

Just. According to formulas and clear simple rules. At the first stage

it is necessary to bring the given equation to the standard form, i.e. to the view:

If the equation is already given to you in this form, you do not need to do the first stage. The most important thing is right

determine all coefficients but, b And c.

Formula for finding the roots of a quadratic equation.

The expression under the root sign is called discriminant . As you can see, to find x, we

use only a, b and c. Those. odds from quadratic equation. Just carefully insert

values a, b and c into this formula and count. Substitute with their signs!

For example, in the equation:

but =1; b = 3; c = -4.

Substitute the values ​​and write:

Example almost solved:

This is the answer.

The most common mistakes are confusion with the signs of values a, b And from. Rather, with substitution

negative values ​​into the formula for calculating the roots. Here the detailed formula saves

with specific numbers. If there are problems with calculations, do it!

Suppose we need to solve the following example:

Here a = -6; b = -5; c = -1

We paint everything in detail, carefully, without missing anything with all the signs and brackets:

Often quadratic equations look slightly different. For example, like this:

Now take note of the practical techniques that dramatically reduce the number of errors.

First reception. Don't be lazy before solving a quadratic equation bring it to standard form.

What does this mean?

Suppose, after any transformations, you get the following equation:

Do not rush to write the formula of the roots! You will almost certainly mix up the odds a, b and c.

Build the example correctly. First, x squared, then without a square, then a free member. Like this:

Get rid of the minus. How? We need to multiply the whole equation by -1. We get:

And now you can safely write down the formula for the roots, calculate the discriminant and complete the example.

Decide on your own. You should end up with roots 2 and -1.

Second reception. Check your roots! By Vieta's theorem.

To solve the given quadratic equations, i.e. if the coefficient

x2+bx+c=0,

thenx 1 x 2 =c

x1 +x2 =−b

For a complete quadratic equation in which a≠1:

x 2 +bx+c=0,

divide the whole equation by but:

→ →

where x 1 And x 2 - roots of the equation.

Reception third. If your equation has fractional coefficients, get rid of the fractions! Multiply

equation for a common denominator.

Output. Practical Tips:

1. Before solving, we bring the quadratic equation to the standard form, build it right.

2. If there is a negative coefficient in front of the x in the square, we eliminate it by multiplying everything

equations for -1.

3. If the coefficients are fractional, we eliminate the fractions by multiplying the entire equation by the corresponding

factor.

4. If x squared is pure, the coefficient for it is equal to one, the solution can be easily checked by

Formulas for the roots of a quadratic equation. The cases of real, multiple and complex roots are considered. Factorization of a square trinomial. Geometric interpretation. Examples of determining roots and factorization.

Basic formulas

Consider the quadratic equation:
(1) .
The roots of a quadratic equation(1) are determined by the formulas:
; .
These formulas can be combined like this:
.
When the roots of the quadratic equation are known, then the polynomial of the second degree can be represented as a product of factors (factored):
.

Further, we assume that are real numbers.
Consider discriminant of a quadratic equation:
.
If the discriminant is positive, then the quadratic equation (1) has two different real roots:
; .
Then the factorization of the square trinomial has the form:
.
If the discriminant is zero, then the quadratic equation (1) has two multiple (equal) real roots:
.
Factorization:
.
If the discriminant is negative, then the quadratic equation (1) has two complex conjugate roots:
;
.
Here is the imaginary unit, ;
and are the real and imaginary parts of the roots:
; .
Then

.

Graphic interpretation

If we graph the function
,
which is a parabola, then the points of intersection of the graph with the axis will be the roots of the equation
.
When , the graph intersects the abscissa axis (axis) at two points.
When , the graph touches the x-axis at one point.
When , the graph does not cross the x-axis.

Below are examples of such graphs.

Useful Formulas Related to Quadratic Equation

(f.1) ;
(f.2) ;
(f.3) .

Derivation of the formula for the roots of a quadratic equation

We perform transformations and apply formulas (f.1) and (f.3):




,
where
; .

So, we got the formula for the polynomial of the second degree in the form:
.
From this it can be seen that the equation

performed at
And .
That is, and are the roots of the quadratic equation
.

Examples of determining the roots of a quadratic equation

Example 1

(1.1) .

Solution

.
Comparing with our equation (1.1), we find the values ​​of the coefficients:
.
Finding the discriminant:
.
Since the discriminant is positive, the equation has two real roots:
;
;
.

From here we obtain the decomposition of the square trinomial into factors:

.

Graph of the function y = 2 x 2 + 7 x + 3 crosses the x-axis at two points.

Let's plot the function
.
The graph of this function is a parabola. It crosses the x-axis (axis) at two points:
And .
These points are the roots of the original equation (1.1).

Answer

;
;
.

Example 2

Find the roots of a quadratic equation:
(2.1) .

Solution

We write the quadratic equation in general form:
.
Comparing with the original equation (2.1), we find the values ​​of the coefficients:
.
Finding the discriminant:
.
Since the discriminant is zero, the equation has two multiple (equal) roots:
;
.

Then the factorization of the trinomial has the form:
.

Graph of the function y = x 2 - 4 x + 4 touches the x-axis at one point.

Let's plot the function
.
The graph of this function is a parabola. It touches the x-axis (axis) at one point:
.
This point is the root of the original equation (2.1). Since this root is factored twice:
,
then such a root is called a multiple. That is, they consider that there are two equal roots:
.

Answer

;
.

Example 3

Find the roots of a quadratic equation:
(3.1) .

Solution

We write the quadratic equation in general form:
(1) .
Let us rewrite the original equation (3.1):
.
Comparing with (1), we find the values ​​of the coefficients:
.
Finding the discriminant:
.
The discriminant is negative, . Therefore, there are no real roots.

You can find complex roots:
;
;
.

Then


.

The graph of the function does not cross the x-axis. There are no real roots.

Let's plot the function
.
The graph of this function is a parabola. It does not cross the abscissa (axis). Therefore, there are no real roots.

Answer

There are no real roots. Complex roots:
;
;
.

Quadratic equation - easy to solve! *Further in the text "KU". Friends, it would seem that in mathematics it can be easier than solving such an equation. But something told me that many people have problems with him. I decided to see how many impressions Yandex gives per request per month. Here's what happened, take a look:

What does it mean? This means that about 70,000 people a month are looking for this information, and this is summer, and what will happen during the school year - there will be twice as many requests. This is not surprising, because those guys and girls who have long graduated from school and are preparing for the exam are looking for this information, and schoolchildren are also trying to refresh their memory.

Despite the fact that there are a lot of sites that tell how to solve this equation, I decided to also contribute and publish the material. Firstly, I want visitors to come to my site on this request; secondly, in other articles, when the speech “KU” comes up, I will give a link to this article; thirdly, I will tell you a little more about his solution than is usually stated on other sites. Let's get started! The content of the article:

A quadratic equation is an equation of the form:

where coefficients a,band with arbitrary numbers, with a≠0.

In the school course, the material is given in the following form - the division of equations into three classes is conditionally done:

1. Have two roots.

2. * Have only one root.

3. Have no roots. It is worth noting here that they do not have real roots

How are roots calculated? Just!

We calculate the discriminant. Under this "terrible" word lies a very simple formula:

The root formulas are as follows:

*These formulas must be known by heart.

You can immediately write down and decide:

Example:

1. If D > 0, then the equation has two roots.

2. If D = 0, then the equation has one root.

3. If D< 0, то уравнение не имеет действительных корней.

Let's look at the equation:

On this occasion, when the discriminant is zero, the school course says that one root is obtained, here it is equal to nine. That's right, it is, but...

This representation is somewhat incorrect. In fact, there are two roots. Yes, yes, do not be surprised, it turns out two equal roots, and to be mathematically accurate, then two roots should be written in the answer:

x 1 = 3 x 2 = 3

But this is so - a small digression. At school, you can write down and say that there is only one root.

Now the following example:

As we know, the root of a negative number is not extracted, so there is no solution in this case.

That's the whole decision process.

Quadratic function.

Here is how the solution looks geometrically. This is extremely important to understand (in the future, in one of the articles, we will analyze in detail the solution of a quadratic inequality).

This is a function of the form:

where x and y are variables

a, b, c are given numbers, where a ≠ 0

The graph is a parabola:

That is, it turns out that by solving a quadratic equation with "y" equal to zero, we find the points of intersection of the parabola with the x-axis. There can be two of these points (the discriminant is positive), one (the discriminant is zero) or none (the discriminant is negative). More about the quadratic function You can view article by Inna Feldman.

Consider examples:

Example 1: Decide 2x 2 +8 x–192=0

a=2 b=8 c= -192

D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Answer: x 1 = 8 x 2 = -12

* You could immediately divide the left and right sides of the equation by 2, that is, simplify it. The calculations will be easier.

Example 2: Solve x2–22 x+121 = 0

a=1 b=-22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

We got that x 1 \u003d 11 and x 2 \u003d 11

In the answer, it is permissible to write x = 11.

Answer: x = 11

Example 3: Solve x 2 –8x+72 = 0

a=1 b= -8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

The discriminant is negative, there is no solution in real numbers.

Answer: no solution

The discriminant is negative. There is a solution!

Here we will talk about solving the equation in the case when a negative discriminant is obtained. Do you know anything about complex numbers? I will not go into detail here about why and where they arose and what their specific role and necessity in mathematics is, this is a topic for a large separate article.

The concept of a complex number.

A bit of theory.

A complex number z is a number of the form

z = a + bi

where a and b are real numbers, i is the so-called imaginary unit.

a+bi is a SINGLE NUMBER, not an addition.

The imaginary unit is equal to the root of minus one:

Now consider the equation:

Get two conjugate roots.

Incomplete quadratic equation.

Consider special cases, this is when the coefficient "b" or "c" is equal to zero (or both are equal to zero). They are solved easily without any discriminants.

Case 1. Coefficient b = 0.

The equation takes the form:

Let's transform:

Example:

4x 2 -16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = -2

Case 2. Coefficient c = 0.

The equation takes the form:

Transform, factorize:

*The product is equal to zero when at least one of the factors is equal to zero.

Example:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 or x–5 =0

x 1 = 0 x 2 = 5

Case 3. Coefficients b = 0 and c = 0.

Here it is clear that the solution to the equation will always be x = 0.

Useful properties and patterns of coefficients.

There are properties that allow solving equations with large coefficients.

butx 2 + bx+ c=0 equality

a + b+ c = 0, then

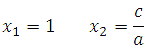
— if for the coefficients of the equation butx 2 + bx+ c=0 equality

a+ with =b, then

These properties help solve a certain kind of equation.

Example 1: 5001 x 2 –4995 x – 6=0

The sum of the coefficients is 5001+( – 4995)+(– 6) = 0, so

Example 2: 2501 x 2 +2507 x+6=0

Equality a+ with =b, means

Regularities of coefficients.

1. If in the equation ax 2 + bx + c \u003d 0 the coefficient "b" is (a 2 +1), and the coefficient "c" is numerically equal to the coefficient "a", then its roots are

ax 2 + (a 2 +1) ∙ x + a \u003d 0 \u003d\u003e x 1 \u003d -a x 2 \u003d -1 / a.

Example. Consider the equation 6x 2 +37x+6 = 0.

x 1 \u003d -6 x 2 \u003d -1/6.

2. If in the equation ax 2 - bx + c \u003d 0, the coefficient "b" is (a 2 +1), and the coefficient "c" is numerically equal to the coefficient "a", then its roots are

ax 2 - (a 2 + 1) ∙ x + a \u003d 0 \u003d\u003e x 1 \u003d a x 2 \u003d 1 / a.

Example. Consider the equation 15x 2 –226x +15 = 0.

x 1 = 15 x 2 = 1/15.

3. If in the equation ax 2 + bx - c = 0 coefficient "b" equals (a 2 – 1), and the coefficient “c” numerically equal to the coefficient "a", then its roots are equal

ax 2 + (a 2 -1) ∙ x - a \u003d 0 \u003d\u003e x 1 \u003d - a x 2 \u003d 1 / a.

Example. Consider the equation 17x 2 + 288x - 17 = 0.

x 1 \u003d - 17 x 2 \u003d 1/17.

4. If in the equation ax 2 - bx - c \u003d 0, the coefficient "b" is equal to (a 2 - 1), and the coefficient c is numerically equal to the coefficient "a", then its roots are

ax 2 - (a 2 -1) ∙ x - a \u003d 0 \u003d\u003e x 1 \u003d a x 2 \u003d - 1 / a.

Example. Consider the equation 10x2 - 99x -10 = 0.

x 1 \u003d 10 x 2 \u003d - 1/10

Vieta's theorem.

Vieta's theorem is named after the famous French mathematician Francois Vieta. Using Vieta's theorem, one can express the sum and product of the roots of an arbitrary KU in terms of its coefficients.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

In sum, the number 14 gives only 5 and 9. These are the roots. With a certain skill, using the presented theorem, you can solve many quadratic equations immediately orally.

Vieta's theorem, moreover. convenient because after solving the quadratic equation in the usual way (through the discriminant), the resulting roots can be checked. I recommend doing this all the time.

TRANSFER METHOD

With this method, the coefficient "a" is multiplied by the free term, as if "transferred" to it, which is why it is called transfer method. This method is used when it is easy to find the roots of an equation using Vieta's theorem and, most importantly, when the discriminant is an exact square.

If but± b+c≠ 0, then the transfer technique is used, for example:

2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)

According to the Vieta theorem in equation (2), it is easy to determine that x 1 \u003d 10 x 2 \u003d 1

The obtained roots of the equation must be divided by 2 (since the two were “thrown” from x 2), we get

x 1 \u003d 5 x 2 \u003d 0.5.

What is the rationale? See what's happening.

The discriminants of equations (1) and (2) are:

If you look at the roots of the equations, then only different denominators are obtained, and the result depends precisely on the coefficient at x 2:

The second (modified) roots are 2 times larger.

Therefore, we divide the result by 2.

*If we roll three of a kind, then we divide the result by 3, and so on.

Answer: x 1 = 5 x 2 = 0.5

sq. ur-ie and the exam.

I will say briefly about its importance - YOU SHOULD BE ABLE TO DECIDE quickly and without thinking, you need to know the formulas of the roots and the discriminant by heart. A lot of the tasks that are part of the USE tasks come down to solving a quadratic equation (including geometric ones).

What is worth noting!

1. The form of the equation can be "implicit". For example, the following entry is possible:

15+ 9x 2 - 45x = 0 or 15x+42+9x 2 - 45x=0 or 15 -5x+10x 2 = 0.

You need to bring it to a standard form (so as not to get confused when solving).

2. Remember that x is an unknown value and it can be denoted by any other letter - t, q, p, h and others.

This topic may seem complicated at first due to the many not-so-simple formulas. Not only do the quadratic equations themselves have long entries, but the roots are also found through the discriminant. There are three new formulas in total. Not very easy to remember. This is possible only after the frequent solution of such equations. Then all the formulas will be remembered by themselves.

General view of the quadratic equation

Here their explicit notation is proposed, when the largest degree is written first, and then - in descending order. Often there are situations when the terms stand apart. Then it is better to rewrite the equation in descending order of the degree of the variable.

Let us introduce notation. They are presented in the table below.

If we accept these notations, all quadratic equations are reduced to the following notation.

Moreover, the coefficient a ≠ 0. Let this formula be denoted by number one.

When the equation is given, it is not clear how many roots will be in the answer. Because one of three options is always possible:

• the solution will have two roots;
• the answer will be one number;
• The equation has no roots at all.

And while the decision is not brought to the end, it is difficult to understand which of the options will fall out in a particular case.

Types of records of quadratic equations

Tasks may have different entries. They will not always look like the general formula of a quadratic equation. Sometimes it will lack some terms. What was written above is the complete equation. If you remove the second or third term in it, you get something different. These records are also called quadratic equations, only incomplete.

Moreover, only the terms for which the coefficients "b" and "c" can disappear. The number "a" cannot be equal to zero under any circumstances. Because in this case the formula turns into a linear equation. The formulas for the incomplete form of the equations will be as follows:

So, there are only two types, in addition to complete ones, there are also incomplete quadratic equations. Let the first formula be number two, and the second number three.

The discriminant and the dependence of the number of roots on its value

This number must be known in order to calculate the roots of the equation. It can always be calculated, no matter what the formula of the quadratic equation is. In order to calculate the discriminant, you need to use the equality written below, which will have the number four.

After substituting the values ​​of the coefficients into this formula, you can get numbers with different signs. If the answer is yes, then the answer to the equation will be two different roots. With a negative number, the roots of the quadratic equation will be absent. If it is equal to zero, the answer will be one.

How is a complete quadratic equation solved?

In fact, consideration of this issue has already begun. Because first you need to find the discriminant. After it is clarified that there are roots of the quadratic equation, and their number is known, you need to use the formulas for the variables. If there are two roots, then you need to apply such a formula.

Since it contains the “±” sign, there will be two values. The expression under the square root sign is the discriminant. Therefore, the formula can be rewritten in a different way.

Formula five. From the same record it can be seen that if the discriminant is zero, then both roots will take the same values.

If the solution of quadratic equations has not yet been worked out, then it is better to write down the values ​​of all coefficients before applying the discriminant and variable formulas. Later this moment will not cause difficulties. But at the very beginning there is confusion.

How is an incomplete quadratic equation solved?

Everything is much simpler here. Even there is no need for additional formulas. And you won't need those that have already been written for the discriminant and the unknown.

First, consider the incomplete equation number two. In this equality, it is supposed to take the unknown value out of the bracket and solve the linear equation, which will remain in the brackets. The answer will have two roots. The first one is necessarily equal to zero, because there is a factor consisting of the variable itself. The second is obtained by solving a linear equation.

The incomplete equation at number three is solved by transferring the number from the left side of the equation to the right. Then you need to divide by the coefficient in front of the unknown. It remains only to extract the square root and do not forget to write it down twice with opposite signs.

The following are some actions that help you learn how to solve all kinds of equalities that turn into quadratic equations. They will help the student to avoid mistakes due to inattention. These shortcomings are the cause of poor grades when studying the extensive topic "Quadric Equations (Grade 8)". Subsequently, these actions will not need to be constantly performed. Because there will be a stable habit.

• First you need to write the equation in standard form. That is, first the term with the largest degree of the variable, and then - without the degree and the last - just a number.

• If a minus appears before the coefficient "a", then it can complicate the work for a beginner to study quadratic equations. It's better to get rid of it. For this purpose, all equality must be multiplied by "-1". This means that all terms will change sign to the opposite.

• In the same way, it is recommended to get rid of fractions. Simply multiply the equation by the appropriate factor so that the denominators cancel out.

Examples

It is required to solve the following quadratic equations:

x 2 - 7x \u003d 0;

15 - 2x - x 2 \u003d 0;

x 2 + 8 + 3x = 0;

12x + x 2 + 36 = 0;

(x+1) 2 + x + 1 = (x+1)(x+2).

The first equation: x 2 - 7x \u003d 0. It is incomplete, therefore it is solved as described for formula number two.

After bracketing, it turns out: x (x - 7) \u003d 0.

The first root takes on the value: x 1 \u003d 0. The second will be found from the linear equation: x - 7 \u003d 0. It is easy to see that x 2 \u003d 7.

Second equation: 5x2 + 30 = 0. Again incomplete. Only it is solved as described for the third formula.

After transferring 30 to the right side of the equation: 5x 2 = 30. Now you need to divide by 5. It turns out: x 2 = 6. The answers will be numbers: x 1 = √6, x 2 = - √6.

Third equation: 15 - 2x - x 2 \u003d 0. Here and below, the solution of quadratic equations will begin by rewriting them into a standard form: - x 2 - 2x + 15 \u003d 0. Now it's time to use the second useful tip and multiply everything by minus one . It turns out x 2 + 2x - 15 \u003d 0. According to the fourth formula, you need to calculate the discriminant: D \u003d 2 2 - 4 * (- 15) \u003d 4 + 60 \u003d 64. It is a positive number. From what was said above, it turns out that the equation has two roots. They need to be calculated according to the fifth formula. According to it, it turns out that x \u003d (-2 ± √64) / 2 \u003d (-2 ± 8) / 2. Then x 1 \u003d 3, x 2 \u003d - 5.

The fourth equation x 2 + 8 + 3x \u003d 0 is converted to this: x 2 + 3x + 8 \u003d 0. Its discriminant is equal to this value: -23. Since this number is negative, the answer to this task will be the following entry: "There are no roots."

The fifth equation 12x + x 2 + 36 = 0 should be rewritten as follows: x 2 + 12x + 36 = 0. After applying the formula for the discriminant, the number zero is obtained. This means that it will have one root, namely: x \u003d -12 / (2 * 1) \u003d -6.

The sixth equation (x + 1) 2 + x + 1 = (x + 1) (x + 2) requires transformations, which consist in the fact that you need to bring like terms, before opening the brackets. In place of the first one there will be such an expression: x 2 + 2x + 1. After equality, this entry will appear: x 2 + 3x + 2. After similar terms are counted, the equation will take the form: x 2 - x \u003d 0. It has become incomplete . Similar to it has already been considered a little higher. The roots of this will be the numbers 0 and 1.

In modern society, the ability to operate with equations containing a squared variable can be useful in many areas of activity and is widely used in practice in scientific and technical developments. This can be evidenced by the design of sea and river vessels, aircraft and missiles. With the help of such calculations, the trajectories of the movement of various bodies, including space objects, are determined. Examples with the solution of quadratic equations are used not only in economic forecasting, in the design and construction of buildings, but also in the most ordinary everyday circumstances. They may be needed on camping trips, at sports events, in stores when shopping and in other very common situations.

Let's break the expression into component factors

The degree of an equation is determined by the maximum value of the degree of the variable that the given expression contains. If it is equal to 2, then such an equation is called a quadratic equation.

If we speak in the language of formulas, then these expressions, no matter how they look, can always be brought to the form when the left side of the expression consists of three terms. Among them: ax 2 (that is, a variable squared with its coefficient), bx (an unknown without a square with its coefficient) and c (free component, that is, an ordinary number). All this on the right side is equal to 0. In the case when such a polynomial does not have one of its constituent terms, with the exception of ax 2, it is called an incomplete quadratic equation. Examples with the solution of such problems, in which the value of the variables is not difficult to find, should be considered first.

If the expression looks in such a way that there are two terms on the right side of the expression, more precisely ax 2 and bx, it is easiest to find x by bracketing the variable. Now our equation will look like this: x(ax+b). Further, it becomes obvious that either x=0, or the problem is reduced to finding a variable from the following expression: ax+b=0. This is dictated by one of the properties of multiplication. The rule says that the product of two factors results in 0 only if one of them is zero.

Example

x=0 or 8x - 3 = 0

As a result, we get two roots of the equation: 0 and 0.375.

Equations of this kind can describe the movement of bodies under the action of gravity, which began to move from a certain point, taken as the origin. Here the mathematical notation takes the following form: y = v 0 t + gt 2 /2. By substituting the necessary values, equating the right side to 0 and finding possible unknowns, you can find out the time elapsed from the moment the body rises to the moment it falls, as well as many other quantities. But we will talk about this later.

Factoring an Expression

The rule described above makes it possible to solve these problems in more complex cases. Consider examples with the solution of quadratic equations of this type.

X2 - 33x + 200 = 0

This square trinomial is complete. First, we transform the expression and decompose it into factors. There are two of them: (x-8) and (x-25) = 0. As a result, we have two roots 8 and 25.

Examples with the solution of quadratic equations in grade 9 allow this method to find a variable in expressions not only of the second, but even of the third and fourth orders.

For example: 2x 3 + 2x 2 - 18x - 18 = 0. When factoring the right side into factors with a variable, there are three of them, that is, (x + 1), (x-3) and (x + 3).

As a result, it becomes obvious that this equation has three roots: -3; -one; 3.

Extracting the square root

Another case of an incomplete second order equation is an expression written in the language of letters in such a way that the right side is built from the components ax 2 and c. Here, to obtain the value of the variable, the free term is transferred to the right side, and after that, the square root is extracted from both sides of the equality. It should be noted that in this case there are usually two roots of the equation. The only exceptions are equalities that do not contain the term c at all, where the variable is equal to zero, as well as variants of expressions when the right side turns out to be negative. In the latter case, there are no solutions at all, since the above actions cannot be performed with roots. Examples of solutions to quadratic equations of this type should be considered.

In this case, the roots of the equation will be the numbers -4 and 4.

Calculation of the area of ​​land

The need for this kind of calculations appeared in ancient times, because the development of mathematics in those distant times was largely due to the need to determine the areas and perimeters of land plots with the greatest accuracy.

We should also consider examples with the solution of quadratic equations compiled on the basis of problems of this kind.

So, let's say there is a rectangular piece of land, the length of which is 16 meters more than the width. You should find the length, width and perimeter of the site, if it is known that its area is 612 m 2.

Getting down to business, at first we will make the necessary equation. Let's denote the width of the section as x, then its length will be (x + 16). It follows from what has been written that the area is determined by the expression x (x + 16), which, according to the condition of our problem, is 612. This means that x (x + 16) \u003d 612.

The solution of complete quadratic equations, and this expression is just that, cannot be done in the same way. Why? Although the left side of it still contains two factors, the product of them is not 0 at all, so other methods are used here.

Discriminant

First of all, we will make the necessary transformations, then the appearance of this expression will look like this: x 2 + 16x - 612 = 0. This means that we have received an expression in the form corresponding to the previously specified standard, where a=1, b=16, c= -612.

This can be an example of solving quadratic equations through the discriminant. Here the necessary calculations are made according to the scheme: D = b 2 - 4ac. This auxiliary value not only makes it possible to find the desired values ​​in the second-order equation, it determines the number of possible options. In case D>0, there are two of them; for D=0 there is one root. In case D<0, никаких шансов для решения у уравнения вообще не имеется.

About roots and their formula

In our case, the discriminant is: 256 - 4(-612) = 2704. This indicates that our problem has an answer. If you know, to, the solution of quadratic equations must be continued using the formula below. It allows you to calculate the roots.

This means that in the presented case: x 1 =18, x 2 =-34. The second option in this dilemma cannot be a solution, because the size of the land plot cannot be measured in negative values, which means that x (that is, the width of the plot) is 18 m. From here we calculate the length: 18+16=34, and the perimeter 2(34+ 18) = 104 (m 2).

Examples and tasks

We continue the study of quadratic equations. Examples and a detailed solution of several of them will be given below.

1) 15x2 + 20x + 5 = 12x2 + 27x + 1

Let's transfer everything to the left side of the equality, make a transformation, that is, we get the form of the equation, which is usually called the standard one, and equate it to zero.

15x 2 + 20x + 5 - 12x 2 - 27x - 1 = 0

Having added similar ones, we determine the discriminant: D \u003d 49 - 48 \u003d 1. So our equation will have two roots. We calculate them according to the above formula, which means that the first of them will be equal to 4/3, and the second 1.

2) Now we will reveal riddles of a different kind.

Let's find out if there are roots x 2 - 4x + 5 = 1 here at all? To obtain an exhaustive answer, we bring the polynomial to the corresponding familiar form and calculate the discriminant. In this example, it is not necessary to solve the quadratic equation, because the essence of the problem is not at all in this. In this case, D \u003d 16 - 20 \u003d -4, which means that there really are no roots.

Vieta's theorem

It is convenient to solve quadratic equations through the above formulas and the discriminant, when the square root is extracted from the value of the latter. But this does not always happen. However, there are many ways to get the values ​​of variables in this case. Example: solving quadratic equations using Vieta's theorem. It is named after a man who lived in 16th-century France and had a brilliant career thanks to his mathematical talent and connections at court. His portrait can be seen in the article.

The pattern that the famous Frenchman noticed was as follows. He proved that the sum of the roots of the equation is equal to -p=b/a, and their product corresponds to q=c/a.

Now let's look at specific tasks.

3x2 + 21x - 54 = 0

For simplicity, let's transform the expression:

x 2 + 7x - 18 = 0

Using the Vieta theorem, this will give us the following: the sum of the roots is -7, and their product is -18. From here we get that the roots of the equation are the numbers -9 and 2. Having made a check, we will make sure that these values ​​of the variables really fit into the expression.

Graph and Equation of a Parabola

The concepts of a quadratic function and quadratic equations are closely related. Examples of this have already been given previously. Now let's look at some mathematical puzzles in a little more detail. Any equation of the described type can be represented visually. Such a dependence, drawn in the form of a graph, is called a parabola. Its various types are shown in the figure below.

Any parabola has a vertex, that is, a point from which its branches come out. If a>0, they go high to infinity, and when a<0, они рисуются вниз. Простейшим примером подобной зависимости является функция y = x 2 . В данном случае в уравнении x 2 =0 неизвестное может принимать только одно значение, то есть х=0, а значит существует только один корень. Это неудивительно, ведь здесь D=0, потому что a=1, b=0, c=0. Выходит формула корней (точнее одного корня) квадратного уравнения запишется так: x = -b/2a.

Visual representations of functions help to solve any equations, including quadratic ones. This method is called graphic. And the value of the x variable is the abscissa coordinate at the points where the graph line intersects with 0x. The coordinates of the vertex can be found by the formula just given x 0 = -b / 2a. And, substituting the resulting value into the original equation of the function, you can find out y 0, that is, the second coordinate of the parabola vertex belonging to the y-axis.

The intersection of the branches of the parabola with the abscissa axis

There are a lot of examples with the solution of quadratic equations, but there are also general patterns. Let's consider them. It is clear that the intersection of the graph with the 0x axis for a>0 is possible only if y 0 takes negative values. And for a<0 координата у 0 должна быть положительна. Для указанных вариантов D>0. Otherwise D<0. А когда D=0, вершина параболы расположена непосредственно на оси 0х.

From the graph of a parabola, you can also determine the roots. The reverse is also true. That is, if it is not easy to get a visual representation of a quadratic function, you can equate the right side of the expression to 0 and solve the resulting equation. And knowing the points of intersection with the 0x axis, it is easier to plot.

From the history

With the help of equations containing a squared variable, in the old days, not only did mathematical calculations and determined the area of ​​\u200b\u200bgeometric shapes. The ancients needed such calculations for grandiose discoveries in the field of physics and astronomy, as well as for making astrological forecasts.

As modern scientists suggest, the inhabitants of Babylon were among the first to solve quadratic equations. It happened four centuries before the advent of our era. Of course, their calculations were fundamentally different from those currently accepted and turned out to be much more primitive. For example, Mesopotamian mathematicians had no idea about the existence of negative numbers. They were also unfamiliar with other subtleties of those known to any student of our time.

Perhaps even earlier than the scientists of Babylon, the sage from India, Baudhayama, took up the solution of quadratic equations. This happened about eight centuries before the advent of the era of Christ. True, the second-order equations, the methods for solving which he gave, were the simplest. In addition to him, Chinese mathematicians were also interested in similar questions in the old days. In Europe, quadratic equations began to be solved only at the beginning of the 13th century, but later they were used in their work by such great scientists as Newton, Descartes and many others.