Основні елементарні функції їхньої властивості. Основні властивості функцій

Повний перелік основних елементарних функцій

До класу основних елементарних функцій належать такі:

1. Постійна функція $y=C$, де $C$ - константа. Така функція приймає те саме значення $C$ за будь-якого $x$.
2. Ступінь функція $y=x^(a) $, де показник ступеня $a$ - дійсне число.
3. Показова функція $y=a^(x) $, де основа ступеня $a>0$, $a\ne 1$.
4. Логарифмічна функція $y=\log _(a) x$, де основа логарифму $a>0$, $a\ne 1$.
5. Тригонометричні функції $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ sec\, x$.
6. Зворотні тригонометричні функції $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , x$.

Ступінні функції

Поведінка статечної функції $y=x^(a) $ розглянемо тих найпростіших випадків, коли її показник ступеня визначає цілочисельне зведення ступінь і витяг кореня.

Випадок 1

Показник ступеня функції $ y = x ^ (a) $ - натуральне число, тобто $ y = x ^ (n) $, $ n \ in N $.

Якщо $n=2\cdot k$ -- парне число, то функція $y=x^(2\cdot k) $ -- парна і необмежено зростає як із необмеженому зростанні аргументу $\left(x\to +\infty \ right)$, так і при необмеженому його спаданні $\left(x\to -\infty \right)$. Таку поведінку функції можна описати виразами $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ і $\mathop(\lim )\limits_(x\to -\infty ) x^(2\cdot k) =+\infty $, які означають, що функція в обох випадках необмежено зростає ($\lim $ - межа). Приклад: графік функції $ y = x ^ (2) $.

Якщо $n=2\cdot k-1$ - непарне число, то функція $y=x^(2\cdot k-1) $ - непарна, необмежено збільшується при необмеженому зростанні аргументу і необмежено зменшується при необмеженому його спаданні. Таку поведінку функції можна описати виразами $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ і $\mathop(\lim )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. Приклад: графік функції $ y = x (3) $.

Випадок 2

Показник ступеня функції $y=x^(a) $ -- ціле негативне число, тобто $y=\frac(1)(x^(n) ) $, $n\in N$.

Якщо $n=2\cdot k$ -- парне число, то функція $y=\frac(1)(x^(2\cdot k) ) $ -- парна та асимптотично (поступово) наближається до нуля як при необмеженому зростанні аргументу, і при необмеженому його спаданні. Таку поведінку функції можна описати єдиним виразом $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$, що означає, що при необмеженому зростанні аргументу по абсолютній величині межа функції дорівнює нулю. Крім того, при прагненні аргументу до нуля як зліва $\left(x\to 0-0\right)$, так і праворуч $\left(x\to 0+0\right)$, функція необмежено зростає. Тому справедливі вирази $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ і $\mathop(\lim )\limits_ (x\to 0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, які означають, що функція $y=\frac(1)(x^(2\cdot k ) ) $ в обох випадках має нескінченну межу, що дорівнює $+\infty $. приклад: графік функції $ y = \ frac (1) (x ^ (2)) $.

Якщо $n=2\cdot k-1$ - непарне число, то функція $y=\frac(1)(x^(2\cdot k-1) ) $ - непарна і асимптотично наближається до нуля як при необмеженому зростанні аргументу, і при необмеженому його спаданні. Таку поведінку функції можна описати єдиним виразом $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$. Крім того, при наближенні аргументу до нуля зліва функція необмежено зменшується, а при наближенні аргументу до нуля праворуч функція необмежено зростає, тобто $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ і $\mathop(\lim )\limits_(x\to 0+0) \frac(1)(x^(2\cdot k-1) ) =+\infty $. приклад: графік функції $ y = \ frac (1) (x) $.

Випадок 3

Показник ступеня функції $ y = x ^ (a) $ - Число, зворотне до натурального, тобто $ y = \ sqrt [(n)] (x) $, $ n \ in N $.

Якщо $n=2\cdot k$ -- парне число, то функція $y=\pm \sqrt[(2\cdot k)](x) $ є двозначною і визначена лише за $x\ge 0$. При необмеженому зростанні аргументу значення функції $y=+\sqrt[(2\cdot k)](x) $ необмежено зростає, а значення функції $y=-\sqrt[(2\cdot k)](x) $ необмежено зменшується тобто $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right)=+\infty $ і $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. Приклад: графік функції $ y = \ pm \ sqrt (x) $.

Якщо $n=2\cdot k-1$ -- непарне число, то функція $y=\sqrt[(2\cdot k-1)](x) $ -- непарна, необмежено зростає при необмеженому зростанні аргументу і необмежено зменшується при необмеженому його зменшується, тобто $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ і $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. Приклад: графік функції $ y = sqrt [(3)] (x) $.

Показова та логарифмічна функції

Показова $y=a^(x) $ та логарифмічна $y=\log _(a) x$ функції є взаємно зворотними. Їхні графіки симетричні щодо загальної бісектриси першого та третього координатних кутів.

При необмеженому зростанні аргументу $\left(x\to +\infty \right)$ показова функція або необмежено зростає $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ , якщо $a>1$, або асимптотично наближається до нуля $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =0$, якщо $a1$, або необмежено зростає $\mathop (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, якщо $a

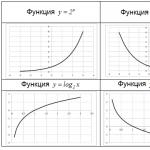
Характерним значенням функції $y=a^(x) $ є значення $x=0$. При цьому всі показові функції незалежно від $a$ обов'язково перетинають вісь $Oy$ при $y=1$. Приклади: графіки функцій $y=2^(x) $ та $y = \left (\frac(1)(2) \right)^(x) $.

Логарифмічна функція $y=\log _(a) x$ визначена лише за $x > 0$.

При необмеженому зростанні аргументу $\left(x\to +\infty \right)$ логарифмічна функція або необмежено зростає $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+\ infty $, якщо $a>1$, або необмежено убуває $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, якщо $a1$, або необмежено зростає $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $, якщо $a

Характерним значенням функції $y=\log _(a) x$ є значення $y=0$. При цьому всі логарифмічні функції незалежно від $a$ обов'язково перетинають вісь $Ox$ при $x=1$. Приклади: графіки функцій $y=log _(2) x$ і $y=log _(1/2) x$.

Деякі логарифмічні функції мають спеціальні позначення. Зокрема, якщо основа логарифму $a=10$, такий логарифм називається десятковим, а відповідна функція записується як $y=\lg x$. А якщо основою логарифму вибирається ірраціональне число $e=2,7182818\ldots$, такий логарифм називається натуральним, а відповідна функція записується як $y=\ln x$. Назад до неї є функція $y=e^(x) $, звана експонентою.

Основними елементарними функціямиє: постійна функція (константа), корінь nступеня, статечна функція, показова, логарифмічна функція, тригонометричні та зворотні тригонометричні функції.

Постійна функція.

Постійна функція задається на множині всіх дійсних чисел формулою , де C- Деяке дійсне число. Постійна функція ставить у відповідність кожному дійсному значенню незалежної змінної xодне й те саме значення залежної змінної y– значення З. Постійну функцію називають константою.

Графіком постійної функції є пряма, паралельна осі абсцис і проходить через точку з координатами (0,C). Наприклад покажемо графіки постійних функцій y=5,y=-2і , яким на малюнку, наведеному нижче, відповідають чорна, червона та синя прямі відповідно.

Властивості постійної функції.

Область визначення: всі множини дійсних чисел.

Постійна функція є парною.

Область значень: безліч, що складається з однини З.

Постійна функція незростаюча і неубутня (на те вона і постійна).

Говорити про опуклість і увігнутість постійної немає сенсу.

Асимптот немає.

Функція проходить через точку (0,C)координатну площину.

Корінь n-ого ступеня.

Розглянемо основну елементарну функцію, яка задається формулою , де n- Натуральне число, більше одиниці.

Корінь n-ого ступеня, n – парне число.

Почнемо з функції корінь n-ого ступеня при парних значеннях показника кореня n.

Для прикладу наведемо малюнок із зображеннями графіків функцій і , їм відповідають чорна, червона та синя лінії.

Аналогічний вигляд мають графіки функцій корінь парного ступеня за інших значень показника.

Властивості функції коріньn -ого ступеня при парнихn .

Корінь n-ого ступеня, n - непарне число.

Функція корінь n-ого ступеня з непарним показником кореня nвизначена на всій множині дійсних чисел. Для прикладу наведемо графіки функцій і , їм відповідають чорна, червона та синя криві.

1) Область визначення функції та область значень функції.

Область визначення функції - це безліч всіх допустимих дійсних значень аргументу x(змінною x), при яких функція y = f(x)визначено. Область значень функції - це безліч усіх дійсних значень y, що приймає функцію.

В елементарної математики вивчаються функції лише з безлічі дійсних чисел.

2) Нулі функції.

Нуль функції – таке значення аргументу, у якому значення функції дорівнює нулю.

3) Проміжки знакостійності функції.

Проміжки знакостійності функції – такі безлічі значень аргументу, у яких значення функції лише позитивні чи лише негативні.

4) Монотонність функції.

Зростаюча функція (у певному проміжку) - функція, яка має більшому значенню аргументу з цього проміжку відповідає більше значення функції.

Зменшуюча функція (у деякому проміжку) - функція, яка має більшому значенню аргументу з цього проміжку відповідає менше значення функції.

5) парність (непарність) функції.

Четна функція - функція, у якої область визначення симетрична щодо початку координат та для будь-якого хв галузі визначення виконується рівність f(-x) = f(x). Графік парної функції симетричний щодо осі ординат.

Непарна функція - функція, у якої область визначення симетрична щодо початку координат та для будь-якого хв галузі визначення справедлива рівність f(-x) = - f(x). Графік непарної функції симетричний щодо початку координат.

6) Обмежена та необмежена функції.

Функція називається обмеженою, якщо є таке позитивне число M, що |f(x)| ≤ M для всіх значень x. Якщо такої кількості немає, то функція - необмежена.

7) Періодичність функції.

Функція f(x) - періодична, якщо існує таке відмінне від нуля число T, що для будь-якого x з області визначення функції має місце: f(x+T) = f(x). Таке найменше називається періодом функції. Усі тригонометричні функції є періодичними. (Тригонометричні формули).

19. Основні елементарні функції, їх властивості та графіки. Застосування функцій економіки.

Основні елементарні функції. Їх властивості та графіки

1. Лінійна функція.

Лінійною функцією називається функція виду , де х - змінна, а і b - дійсні числа.

Число аназивають кутовим коефіцієнтом прямої, він дорівнює тангенсу кута нахилу цієї прямої до позитивного напрямку осі абсцис. Графік лінійної функції є пряма лінія. Вона визначається двома точками.

Властивості лінійної функції

1. Область визначення - безліч всіх дійсних чисел: Д(y) = R

2. Безліч значень - безліч всіх дійсних чисел: Е(у) = R

3. Функція набуває нульового значення при або.

4. Функція зростає (зменшується) по всій області визначення.

5. Лінійна функція безперервна по всій області визначення, диференційована і .

2. Квадратична функція.

Функція виду , де х – змінна, коефіцієнти а, b, с – дійсні числа, називається квадратичні.

Розглядаючи функції комплексного змінного, Ліувілль визначив елементарні функції дещо ширше. Елементарна функція yзмінної x- аналітична функція, яка може бути представлена ​​як алгебраїчна функція від xта функцій , причому є логарифмом або експонентою від деякої функції алгебри g 1 від x .

Наприклад, sin( x) - алгебраїчна функція від e ix .

Не обмежуючи спільності розгляду, можна вважати функції алгебраїчно незалежні, тобто якщо рівняння алгебри виконується для всіх x, то всі коефіцієнти полінома рівні нулю.

Диференціювання елементарних функцій

де z 1 "(z) одно або g 1 " / g 1 або z 1 g 1 " залежно від того, чи логарифм z 1 або експонента і т. д. На практиці зручно використовувати таблицю похідних.

Інтегрування елементарних функцій

Теорема Ліувіля є основою для створення алгоритмів символьного інтегрування елементарних функцій, що реалізуються, напр.

Обчислення меж

Теорія Ліувіля не поширюється на обчислення меж. Не відомо, чи існує алгоритм, який за заданою елементарною формулою послідовності дає відповідь, має вона межу чи ні. Наприклад, відкрите питання про те, чи сходиться послідовність .

Література

• J. Liouville. Mémoire sur l’integration d’une classe de fonctions transcendantes// J. Reine Angew. Math. Bd. 13, p. 93-118. (1835)
• JF. Ritt. Integration in Finite Terms. N.-Y., 1949 // http://lib.homelinux.org
• А. Г. Хованський. Топологічна теорія Галуа: розв'язність та нерозв'язність рівнянь у кінцевому виглядіГол. 1. M, 2007

Примітки

Wikimedia Foundation. 2010 .

• Елементарне збудження
• Елементарний результат

Дивитись що таке "Елементарна функція" в інших словниках:

елементарна функція- Функція, яка, якщо її поділити на дрібніші функції, не може бути однозначно визначена в ієрархії цифрової передачі. Отже, з погляду мережі вона є неподільною (МСЕ T G.806). Тематики електрозв'язок, основні поняття EN adaptation functionA … Довідник технічного перекладача

функція взаємодії між рівнями мережі- Елементарна функція, що забезпечує взаємодію характеристичної інформації між двома рівнями мережі. (МСЕ T G.806). Тематики електрозв'язок, основні поняття EN layer. Довідник технічного перекладача