Aritmetični kvadratni koren in njegove lastnosti.

Ta članek je zbirka podrobnih informacij, ki obravnavajo temo lastnosti korenin. Glede na temo bomo začeli z lastnostmi, preučili vse formulacije in podali dokaze. Za utrjevanje teme bomo upoštevali lastnosti n-te stopnje.

Yandex.RTB R-A-339285-1

Lastnosti korena

Govorili bomo o nepremičninah.

Lastnina pomnožene številke a in b, ki je predstavljena kot enakost a · b = a · b . Lahko se predstavi kot množitelji, pozitivni ali enaki nič a 1, a 2, …, a k kot a 1 a 2 … a k = a 1 a 2 … a k ;
iz zasebnega a: b = a: b, a ≥ 0, b > 0, lahko zapišemo tudi v tej obliki a b = a b ;
Lastnost iz moči števila a s sodim eksponentom a 2 m = a m za katero koli število a, na primer lastnost iz kvadrata števila a 2 = a .

V kateri koli od predstavljenih enačb lahko zamenjate dele pred in za znakom pomišljaja, na primer enakost a · b = a · b se pretvori kot a · b = a · b . Lastnosti enakosti se pogosto uporabljajo za poenostavitev kompleksnih enačb.

Dokaz prvih lastnosti temelji na definiciji kvadratni koren in lastnosti potenk z naravnim eksponentom. Za utemeljitev tretje lastnosti se je treba sklicevati na definicijo modula števila.

Najprej je treba dokazati lastnosti kvadratnega korena a · b = a · b . Po definiciji je treba upoštevati, da je a b število, pozitivno ali enako nič, ki bo enako a b med gradnjo v kvadrat. Vrednost izraza a · b je pozitivna ali enaka nič kot zmnožek nenegativnih števil. Lastnost stopnje pomnoženih števil nam omogoča, da enakost predstavimo v obliki (a · b) 2 = a 2 · b 2 . Po definiciji kvadratnega korena a 2 \u003d a in b 2 \u003d b, nato a b \u003d a 2 b 2 \u003d a b.

Na podoben način je to mogoče dokazati iz izdelka k multiplikatorji a 1, a 2, …, a k bo enak zmnožku kvadratnih korenov teh faktorjev. Dejansko je a 1 · a 2 · … · ak 2 = a 1 2 · a 2 2 · … · ak 2 = a 1 · a 2 · … · a k .

Iz te enakosti sledi, da je a 1 · a 2 · … · a k = a 1 · a 2 · … · a k .

Oglejmo si nekaj primerov za okrepitev teme.

Primer 1

3 5 2 5 = 3 5 2 5 , 4 , 2 13 1 2 = 4 , 2 13 1 2 in 2 , 7 4 12 17 0 , 2 (1) = 2 , 7 4 12 17 0. 2 (1) .

Treba je dokazati lastnost aritmetičnega kvadratnega korena količnika: a: b = a: b, a ≥ 0, b > 0. Lastnost vam omogoča, da zapišete enakost a: b 2 \u003d a 2: b 2 in a 2: b 2 \u003d a: b, medtem ko je a: b pozitivno število ali enako nič. Ta izraz bo dokaz.

Na primer, 0:16 = 0:16, 80:5 = 80:5 in 30, 121 = 30, 121.

Upoštevajte lastnost kvadratnega korena kvadrata števila. Lahko ga zapišemo kot enakost kot 2 = a Za dokaz te lastnosti je treba podrobno preučiti več enakosti za a ≥ 0 in pri a< 0 .

Očitno je za a ≥ 0 enakost a 2 = a resnična. Pri a< 0 enakost a 2 = - a bo resnična. Pravzaprav v tem primeru − a > 0 in (− a) 2 = a 2 . Sklepamo lahko, da je a 2 = a , a ≥ 0 - a , a< 0 = a . Именно это и требовалось доказать.

Poglejmo si nekaj primerov.

Primer 2

5 2 = 5 = 5 in - 0. 36 2 = - 0. 36 = 0. 36.

Dokazana lastnost bo pomagala utemeljiti a 2 m = a m , kjer a- pravi in m- naravno število. Dejansko nam lastnost eksponentiranja omogoča zamenjavo stopnje a 2 m izražanje (dopoldan) 2, potem a 2 · m = (a m) 2 = a m .

Primer 3

3 8 = 3 4 = 3 4 in (- 8 , 3) 14 = - 8 , 3 7 = (8 , 3) 7 .

Lastnosti n-toga korena

Najprej morate upoštevati glavne lastnosti korenin n-te stopnje:

Lastnost iz produkta števil a in b, ki so pozitivni ali enaki nič, lahko izrazimo kot enakost a b n = a n b n , ta lastnost velja za produkt kštevilke a 1, a 2, …, a k kot a 1 a 2 … a k n = a 1 n a 2 n … a k n ;
od ulomno število ima lastnost a b n = a n b n , kjer a- kaj pravo število, ki je pozitiven ali enak nič, in b je pozitivno realno število;
Za katero koli a in sode številke n = 2 m a 2 m 2 m = a je res in za liho n = 2 m − 1 izpolnjena je enakost a 2 · m - 1 2 · m - 1 = a.
Lastnost ekstrakcije iz a m n = a n m , kjer a- poljubno število, pozitivno ali enako nič, n in m so naravna števila, to lastnost lahko predstavimo tudi kot . . a n k n 2 n 1 = a n 1 · n 2 . . . nk ;
Za vsako nenegativno a in poljubno n in m, ki so naravni, lahko definiramo tudi pravično enakost a m n · m = a n ;
lastnost stopnje n iz moči števila a, ki je pozitiven ali enak nič, v naravi m, opredeljeno z enakostjo a m n = a n m ;
Primerjalna lastnost, ki imajo enake eksponente: za vsa pozitivna števila a in b tako da a< b , neenakost a n< b n ;
Primerjalna lastnost, ki jo imajo enake številke koren: če m in n- naravna števila, ki m > n, nato pri 0 < a < 1 velja neenakost a m > a n in za a > 1 a m< a n .

Zgornje enačbe veljajo, če so deli pred in za znakom enakosti obrnjeni. Uporabljajo se lahko tudi v tej obliki. To se pogosto uporablja pri poenostavitvi ali preoblikovanju izrazov.

Dokaz zgornjih lastnosti korena temelji na definiciji, lastnostih stopnje in definiciji modula števila. Te lastnosti je treba dokazati. Ampak vse je v redu.

Najprej bomo dokazali lastnosti korena n-te stopnje iz produkta a · b n = a n · b n . Za a in b, ki so pozitiven ali nič , tudi vrednost a n · b n je pozitivna ali enaka nič, saj je posledica množenja nenegativnih števil. Lastnost naravnega produkta moči nam omogoča, da zapišemo enakost a n · b n n = a n n · b n n . Po definiciji korena n stopnja a n n = a in b n n = b , torej a n · b n n = a · b . Nastala enakost je točno tisto, kar je bilo potrebno dokazati.

Ta lastnost je podobno dokazana za izdelek k faktorji: za nenegativna števila a 1 , a 2 , … , a n a 1 n · a 2 n · … · a k n ≥ 0 .

Tukaj so primeri uporabe korenske lastnosti n th potenca iz produkta: 5 2 1 2 7 = 5 7 2 1 2 7 in 8 , 3 4 17 , (21) 4 3 4 5 7 4 = 8 , 3 17 , (21) 3 5 7 4 .

Dokažimo lastnost korena kvocienta a b n = a n b n . Pri a ≥ 0 in b > 0 pogoj a n b n ≥ 0 je izpolnjen in a n b n n = a n n b n n = a b .

Pokažimo primere:

Primer 4

8 27 3 = 8 3 27 3 in 2 , 3 10: 2 3 10 = 2 , 3: 2 3 10 .

Za naslednji korak je treba dokazati lastnosti n-te stopnje od števila do stopnje n. To predstavljamo kot enakost a 2 m 2 m = a in a 2 m - 1 2 m - 1 = a za katero koli realno a in naravno m. Pri a ≥ 0 dobimo a = a in a 2 m = a 2 m , kar dokazuje enakost a 2 m 2 m = a , enakost a 2 m - 1 2 m - 1 = a pa je očitna. Pri a< 0 dobimo a = - a in a 2 m = (- a) 2 m = a 2 m . Zadnja transformacija števila velja glede na lastnost stopnje. To dokazuje enakost a 2 m 2 m \u003d a in a 2 m - 1 2 m - 1 \u003d a bo res, saj - c 2 m - 1 = - c 2 m velja za liho stopnja - 1 za poljubno število c , pozitiven ali enak nič.

Za konsolidacijo prejetih informacij razmislite o nekaj primerih uporabe lastnosti:

Primer 5

7 4 4 = 7 = 7 , (- 5) 12 12 = - 5 = 5 , 0 8 8 = 0 = 0 , 6 3 3 = 6 in (- 3 , 39) 5 5 = - 3 , 39 .

Dokažimo naslednjo enakost a m n = a n · m . Če želite to narediti, morate spremeniti števila pred znakom enakosti in za njim na mestih a n · m = a m n . To bo označevalo pravilen vnos. Za a , kar je pozitivno ali enako nič , oblike a m n je pozitivno število oz nič. Obrnimo se na lastnost dviga potenca na potenco in definicijo. Z njihovo pomočjo lahko pretvorite enakosti v obliki a m n n · m = a m n n m = a m m = a . To dokazuje obravnavano lastnost korena iz korena.

Druge lastnosti so dokazane podobno. Resnično,. . . a n k n 2 n 1 n 1 n 2 . . . nk = . . . a n k n 3 n 2 n 2 n 3 . . . nk = . . . a nk n 4 n 3 n 3 n 4 . . . nk = . . . = a n k n k = a .

Na primer, 7 3 5 = 7 5 3 in 0, 0009 6 = 0, 0009 2 2 6 = 0, 0009 24.

Dokažimo naslednjo lastnost a m n · m = a n . Za to je treba pokazati, da je n število, ki je pozitivno ali enako nič. Ko se dvigne na potenco, je n m a m. Če številka a je torej pozitiven ali nič n th stopnje od med a je pozitivno število ali enako nič. Poleg tega je a n · m n = a n n m , kar je bilo treba dokazati.

Za utrjevanje pridobljenega znanja si oglejte nekaj primerov.

Dokažimo naslednjo lastnost - lastnost korena potence oblike a m n = a n m . Očitno je, da pri a ≥ 0 stopnja a n m je nenegativno število. Še več, njo n-th stopnja je enaka a m, dejansko, a n m n = a n m · n = a n n m = a m . To dokazuje obravnavano lastnost diplome.

Na primer, 2 3 5 3 = 2 3 3 5 .

To moramo dokazati za vsa pozitivna števila a in b a< b . Razmislite o neenakosti a n< b n . Воспользуемся методом от противного a n ≥ b n . Тогда, согласно свойству, о котором говорилось выше, неравенство считается верным a n n ≥ b n n , то есть, a ≥ b . Но это не соответствует условию a< b . Zato je n< b n при a< b .

Na primer, damo 12 4< 15 2 3 4 .

Upoštevajte lastnost korena n-. stopnja. Najprej razmislite o prvem delu neenakosti. Pri m > n in 0 < a < 1 res a m > a n . Recimo, da je m ≤ a n. Lastnosti bodo poenostavile izraz na a n m · n ≤ a m m · n . Potem je glede na lastnosti stopnje z naravnim eksponentom izpolnjena neenakost a n m n m n ≤ a m m n m n, tj. a n ≤ a m. Vrednost, pridobljena pri m > n in 0 < a < 1 se ne ujema z zgornjimi lastnostmi.

Na enak način je to mogoče dokazati m > n in a > 1 stanje a m< a n .

Če želite popraviti zgornje lastnosti, razmislite o nekaterih konkretni primeri. Razmislite o neenakosti z uporabo določenih številk.

Primer 6

0 , 7 3 < 0 , 7 5 и 12 > 12 7 .

Če opazite napako v besedilu, jo označite in pritisnite Ctrl+Enter

Površina kvadratnega zemljišča je 81 dm². Poiščite njegovo stran. Recimo, da je dolžina stranice kvadrata X decimetrov. Potem je površina parcele X² kvadratnih decimetrov. Ker je ta površina glede na pogoj 81 dm², torej X² = 81. Dolžina stranice kvadrata je pozitivno število. Pozitivno število, katerega kvadrat je 81, je število 9. Pri reševanju naloge je bilo treba najti število x, katerega kvadrat je 81, torej rešiti enačbo X² = 81. Ta enačba ima dva korena: x 1 = 9 in x 2 = - 9, saj je 9² = 81 in (- 9)² = 81. Obe številki 9 in - 9 se imenujeta kvadratni koreni števila 81.

Upoštevajte, da je eden od kvadratnih korenov X= 9 je pozitivno število. Imenuje se aritmetični kvadratni koren iz 81 in je označen z √81, torej √81 = 9.

Aritmetični kvadratni koren iz števila a je nenegativno število, katerega kvadrat je enak a.

Na primer, številki 6 in -6 sta kvadratni koreni iz 36. Število 6 je aritmetični kvadratni koren iz 36, saj je 6 nenegativno število in 6² = 36. Število -6 ni aritmetični koren.

Aritmetični kvadratni koren iz števila a označena takole: √ a.

Znak se imenuje aritmetični kvadratni korenski znak; a se imenuje korenski izraz. Izraz √ a preberite takole: aritmetični kvadratni koren iz števila a. Na primer, √36 = 6, √0 = 0, √0,49 = 0,7. V primerih, ko je jasno, da govorimo o aritmetičnem korenu na kratko pravijo: "kvadratni koren iz a«.

Dejanje iskanja kvadratnega korena iz števila se imenuje odvzem kvadratnega korena. To dejanje je obratno od kvadrature.

Vsako število je lahko na kvadrat, vendar ni vsako število kvadratni koren. Na primer, nemogoče je izluščiti kvadratni koren števila - 4. Če je tak koren obstajal, ga označite s črko X, bi dobili napačno enakost x² \u003d - 4, saj je na levi strani nenegativno število, na desni pa negativno število.

Izraz √ a smiselno le takrat a ≥ 0. Definicijo kvadratnega korena lahko na kratko zapišemo kot: √ a ≥ 0, (√a)² = a. Enakost (√ a)² = a velja za a ≥ 0. Tako se zagotovi, da je kvadratni koren nenegativnega števila a enaka b, to je, da √ a =b, morate preveriti, ali sta izpolnjena naslednja dva pogoja: b ≥ 0, b² = a.

Kvadratni koren ulomka

Izračunajmo. Upoštevajte, da je √25 = 5, √36 = 6, in preverite, ali enakost velja.

Ker in , potem je enakost resnična. torej .

izrek:Če a≥ 0 in b> 0, to je koren ulomka enaka korenu iz števca, deljeno s korenom imenovalca. Treba je dokazati, da: in .

Ker √ a≥0 in √ b> 0, potem .

Z lastnostjo povišanja ulomka na potenco in določanja kvadratnega korena izrek je dokazan. Poglejmo si nekaj primerov.

Izračunaj po dokazanem izreku .

Drugi primer: Dokaži to , če a ≤ 0, b < 0. .

Drug primer: Izračunaj.

Transformacija kvadratnega korena

Odvzem množitelja izpod znaka korena. Naj bo podan izraz. Če a≥ 0 in b≥ 0, potem lahko po izreku o korenu produkta zapišemo:

Takšna transformacija se imenuje faktorje iz korenskega znaka. Razmislite o primeru;

Izračunajte pri X= 2. Neposredna zamenjava X= 2 v radikalnem izrazu vodi do zapletenih izračunov. Te izračune lahko poenostavimo, če najprej odstranimo faktorje izpod predznaka korena: . Zdaj, če zamenjamo x = 2, dobimo:.

Torej, ko vzamemo faktor izpod predznaka korena, je radikalni izraz predstavljen kot produkt, v katerem je eden ali več faktorjev kvadrati nenegativnih števil. Nato se uporabi izrek o korenskem produktu in vzame se koren vsakega faktorja. Razmislite o primeru: Poenostavite izraz A = √8 + √18 - 4√2 tako, da vzamete faktorje izpod predznaka korena v prvih dveh členih, dobimo:. Poudarjamo, da je enakost velja samo takrat a≥ 0 in b≥ 0. če a < 0, то .

Dejstvo 1.
\(\bullet\) Vzemite neko nenegativno število \(a\) (tj. \(a\geqslant 0\) ). Nato (aritmetika) kvadratni koren iz števila \(a\) se imenuje takšno nenegativno število \(b\), ko ga kvadriramo, dobimo število \(a\): \[\sqrt a=b\quad \text(enako kot)\quad a=b^2\] Iz definicije izhaja, da \(a\geqslant 0, b\geqslant 0\). Te omejitve so pomemben pogoj obstoj kvadratnega korena in jih je treba zapomniti!
Spomnimo se, da vsako število, če je kvadratno, daje nenegativen rezultat. To pomeni, \(100^2=10000\geqslant 0\) in \((-100)^2=10000\geqslant 0\) .
\(\bullet\) Kaj je \(\sqrt(25)\) ? Vemo, da je \(5^2=25\) in \((-5)^2=25\) . Ker moramo po definiciji najti nenegativno število, potem \(-5\) ni primeren, zato \(\sqrt(25)=5\) (ker \(25=5^2\) ).
Iskanje vrednosti \(\sqrt a\) se imenuje odvzem kvadratnega korena števila \(a\) , število \(a\) pa korenski izraz.
\(\bullet\) Glede na definicijo so izrazi \(\sqrt(-25)\) , \(\sqrt(-4)\) itd. nima smisla.

Dejstvo 2.
Za hitre izračune se bo koristno naučiti tabele kvadratov naravna števila od \(1\) do \(20\): \[\begin(array)(|ll|) \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13 ^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^ 2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2= 400\\ \hline \end(array)\]

Dejstvo 3.
Kaj je mogoče narediti s kvadratnimi koreninami?
\(\bullet\) Vsota ali razlika kvadratnih korenov NI ENAKA kvadratnemu korenu vsote ali razlike, t.j. \[\sqrt a\pm\sqrt b\ne \sqrt(a\pm b)\] Tako, če morate izračunati na primer \(\sqrt(25)+\sqrt(49)\) , potem morate najprej najti vrednosti \(\sqrt(25)\) in \(\sqrt (49)\ ) in jih nato seštejte. posledično \[\sqrt(25)+\sqrt(49)=5+7=12\] Če vrednosti \(\sqrt a\) ali \(\sqrt b\) ni mogoče najti pri dodajanju \(\sqrt a+\sqrt b\), se tak izraz ne pretvori naprej in ostane takšen, kot je. Na primer, v vsoti \(\sqrt 2+ \sqrt (49)\) lahko najdemo \(\sqrt(49)\) - to je \(7\) , vendar \(\sqrt 2\) ne more biti na kakršen koli način preoblikovan, zato \(\sqrt 2+\sqrt(49)=\sqrt 2+7\). Poleg tega tega izraza na žalost ni mogoče na noben način poenostaviti.\(\bullet\) Zmnožek/količnik kvadratnih korenov je enak kvadratnemu korenu produkta/količnika, t.j. \[\sqrt a\cdot \sqrt b=\sqrt(ab)\quad \text(s)\quad \sqrt a:\sqrt b=\sqrt(a:b)\] (pod pogojem, da sta oba dela enakosti smiselna)
Primer: \(\sqrt(32)\cdot \sqrt 2=\sqrt(32\cdot 2)=\sqrt(64)=8\); \(\sqrt(768):\sqrt3=\sqrt(768:3)=\sqrt(256)=16\); \(\sqrt((-25)\cdot (-64))=\sqrt(25\cdot 64)=\sqrt(25)\cdot \sqrt(64)= 5\cdot 8=40\). \(\bullet\) S temi lastnostmi je priročno poiskati kvadratne korene velike številke tako da jih faktoriziramo.
Razmislite o primeru. Poiščite \(\sqrt(44100)\) . Ker \(44100:100=441\) , potem \(44100=100\cdot 441\) . Glede na kriterij deljivosti je število \(441\) deljivo z \(9\) (ker je vsota njegovih števk 9 in je deljiva z 9), torej \(441:9=49\) , to je \(441=9\ cdot 49\) .
Tako smo dobili: \[\sqrt(44100)=\sqrt(9\cdot 49\cdot 100)= \sqrt9\cdot \sqrt(49)\cdot \sqrt(100)=3\cdot 7\cdot 10=210\] Poglejmo si še en primer: \[\sqrt(\dfrac(32\cdot 294)(27))= \sqrt(\dfrac(16\cdot 2\cdot 3\cdot 49\cdot 2)(9\cdot 3))= \sqrt( \ dfrac(16\cdot4\cdot49)(9))=\dfrac(\sqrt(16)\cdot \sqrt4 \cdot \sqrt(49))(\sqrt9)=\dfrac(4\cdot 2\cdot 7)3 =\dfrac(56)3\]
\(\bullet\) Na primeru izraza \(5\sqrt2\) (okrajšava za izraz \(5\cdot \sqrt2\) bomo pokazali, kako vnesti številke pod znakom kvadratnega korena). Ker \(5=\sqrt(25)\) , potem \ Upoštevajte tudi, da npr.
1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .

zakaj je tako? Pojasnimo s primerom 1). Kot ste že razumeli, ne moremo nekako pretvoriti števila \(\sqrt2\) . Predstavljajte si, da je \(\sqrt2\) neko število \(a\) . V skladu s tem izraz \(\sqrt2+3\sqrt2\) ni nič drugega kot \(a+3a\) (eno število \(a\) plus še tri enaka števila \(a\) ). In vemo, da je to enako štirim takim številkam \(a\) , to je \(4\sqrt2\) .

Dejstvo 4.
\(\bullet\) Pogosto se reče "ne morem izvleči korena", ko se pri iskanju vrednosti nekega števila ni mogoče znebiti znaka \(\sqrt () \ \) korena (radikala). Na primer, lahko korenite število \(16\), ker \(16=4^2\) , torej \(\sqrt(16)=4\) . Toda izvleči koren iz števila \(3\) , torej najti \(\sqrt3\) , je nemogoče, ker ni takšnega števila, ki bi na kvadrat dalo \(3\) .
Takšna števila (ali izrazi s takšnimi številkami) so iracionalni. Na primer številke \(\sqrt3, \ 1+\sqrt2, \ \sqrt(15)\) itd. so iracionalni.
Neracionalna so tudi števila \(\pi\) (število "pi", približno enako \(3,14\)), \(e\) (to število se imenuje Eulerjevo število, približno enako \(2). ,7\) ) itd.
\(\bullet\) Upoštevajte, da bo vsako število racionalno ali iracionalno. In skupaj vse racionalno in vse iracionalna števila tvorijo niz, ki se imenuje niz realnih (realnih) števil. Ta niz je označen s črko \(\mathbb(R)\) .
To pomeni, da so vse številke, ki so ta trenutek vemo, da se imenujejo realna števila.

Dejstvo 5.
\(\bullet\) Modul realnega števila \(a\) je nenegativno število \(|a|\), enako razdalji od točke \(a\) do \(0\) na realnem vrstico. Na primer, \(|3|\) in \(|-3|\) sta enaki 3, saj sta razdalji od točk \(3\) in \(-3\) do \(0\) enaki enako in enako \(3 \) .
\(\bullet\) Če je \(a\) nenegativno število, potem \(|a|=a\) .
Primer: \(|5|=5\) ; \(\qquad |\sqrt2|=\sqrt2\) . \(\bullet\) Če je \(a\) negativno število, potem \(|a|=-a\) .
Primer: \(|-5|=-(-5)=5\) ; \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Pravijo, da za negativna števila modul "poje" minus, pozitivna števila, pa tudi število \(0\) , modul ostane nespremenjen.
AMPAK to pravilo velja samo za številke. Če imate pod znakom modula neznano \(x\) (ali kakšno drugo neznano), na primer \(|x|\) , za katero ne vemo, ali je pozitivna, enaka nič ali negativna, potem znebiti se modula ne moremo. V tem primeru ta izraz ostane tak: \(|x|\) . \(\bullet\) Veljajo naslednje formule: \[(\large(\sqrt(a^2)=|a|))\] \[(\large((\sqrt(a))^2=a)), \text( zagotovljeno) a\geqslant 0\] Pogosto se naredi naslednja napaka: pravijo, da sta \(\sqrt(a^2)\) in \((\sqrt a)^2\) ista stvar. To velja samo, če je \(a\) pozitivno število ali nič. Če pa je \(a\) negativno število, potem to ni res. Dovolj je, da razmislimo o takem primeru. Vzemimo številko \(-1\) namesto \(a\). Potem \(\sqrt((-1)^2)=\sqrt(1)=1\) , vendar izraz \((\sqrt (-1))^2\) sploh ne obstaja (ker je nemogoče pod znak korena vpiši negativne številke!).
Zato vas opozarjamo na dejstvo, da \(\sqrt(a^2)\) ni enako \((\sqrt a)^2\) ! Primer: 1) \(\sqrt(\left(-\sqrt2\right)^2)=|-\sqrt2|=\sqrt2\), Ker \(-\sqrt2<0\) ;

\(\fantom(00000)\) 2) \((\sqrt(2))^2=2\) . \(\bullet\) Ker \(\sqrt(a^2)=|a|\) , potem je \[\sqrt(a^(2n))=|a^n|\] (izraz \(2n\) označuje sodo število)
To pomeni, da se pri izločanju korena iz števila, ki je v neki stopnji, ta stopnja prepolovi.
Primer:
1) \(\sqrt(4^6)=|4^3|=4^3=64\)
2) \(\sqrt((-25)^2)=|-25|=25\) (upoštevajte, da če modul ni nastavljen, se izkaže, da je koren števila enak \(-25) \) ; vendar se spomnimo, kar po definiciji korena to ne more biti: pri ekstrakciji korena moramo vedno dobiti pozitivno število ali nič)
3) \(\sqrt(x^(16))=|x^8|=x^8\) (ker katero koli število na sodo potenco ni negativno)

Dejstvo 6.
Kako primerjati dva kvadratna korena?
\(\bullet\) Velja za kvadratne korene: če \(\sqrt a<\sqrt b\) , то \(aPrimer:
1) primerjaj \(\sqrt(50)\) in \(6\sqrt2\) . Najprej pretvorimo drugi izraz v \(\sqrt(36)\cdot \sqrt2=\sqrt(36\cdot 2)=\sqrt(72)\). Tako od \(50<72\) , то и \(\sqrt{50}<\sqrt{72}\) . Следовательно, \(\sqrt{50}<6\sqrt2\) .
2) Med katerimi celimi števili je \(\sqrt(50)\) ?
Ker \(\sqrt(49)=7\) , \(\sqrt(64)=8\) in \(49<50<64\) , то \(7<\sqrt{50}<8\) , то есть число \(\sqrt{50}\) находится между числами \(7\) и \(8\) .
3) Primerjaj \(\sqrt 2-1\) in \(0,5\) . Recimo \(\sqrt2-1>0,5\) : \[\begin(poravnano) &\sqrt 2-1>0,5 \ \big| +1\quad \text((dodaj enega na obe strani))\\ &\sqrt2>0,5+1 \ \big| \ ^2 \quad\text((kvadrat oba dela))\\ &2>1,5^2\\ &2>2,25 \end(poravnano)\] Vidimo, da smo dobili napačno neenakost. Zato je bila naša domneva napačna in \(\sqrt 2-1<0,5\) .
Upoštevajte, da dodajanje določenega števila obema stranema neenakosti ne vpliva na njen predznak. Množenje/deljenje obeh strani neenakosti s pozitivnim številom prav tako ne spremeni njenega predznaka, vendar množenje/deljenje z negativnim številom obrne predznak neenakosti!
Obe strani enačbe/neenakosti je mogoče kvadrirati SAMO, ČE obe strani nista negativni. Na primer, v neenakosti iz prejšnjega primera lahko kvadrirate obe strani, v neenakosti \(-3<\sqrt2\) нельзя (убедитесь в этом сами)! \(\bullet\) Upoštevajte to \[\začetek(poravnano) &\sqrt 2\približno 1,4\\ &\sqrt 3\približno 1,7 \end(poravnano)\] Poznavanje približnega pomena teh številk vam bo pomagalo pri primerjavi številk! \(\bullet\) Če želite iz nekega velikega števila, ki ga ni v tabeli kvadratov, izluščiti koren (če je izvlečen), morate najprej določiti, med katerimi "stotinami" je, nato med katerimi "deseticami", in nato določi zadnjo številko tega števila. Pokažimo, kako deluje s primerom.
Vzemite \(\sqrt(28224)\) . Vemo, da \(100^2=10\,000\) , \(200^2=40\,000\) in tako naprej. Upoštevajte, da je \(28224\) med \(10\,000\) in \(40\,000\) . Zato je \(\sqrt(28224)\) med \(100\) in \(200\) .
Zdaj pa določimo, med katerimi "deseticami" je naše število (to je na primer med \(120\) in \(130\) ). Iz tabele kvadratov vemo tudi, da \(11^2=121\) , \(12^2=144\) itd., nato \(110^2=12100\) , \(120^2=14400 \ ) , \(130^2=16900\) , \(140^2=19600\) , \(150^2=22500\) , \(160^2=25600\) , \(170^2=28900 \ ) . Tako vidimo, da je \(28224\) med \(160^2\) in \(170^2\) . Zato je število \(\sqrt(28224)\) med \(160\) in \(170\) .
Poskusimo določiti zadnjo številko. Spomnimo se, katera enomestna števila pri kvadriranju dajejo na koncu \ (4 \) ? To sta \(2^2\) in \(8^2\) . Zato se bo \(\sqrt(28224)\) končal z 2 ali 8. Preverimo to. Poiščite \(162^2\) in \(168^2\):
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\) .
Zato \(\sqrt(28224)=168\) . Voila!

Za ustrezno reševanje izpita iz matematike je treba najprej preučiti teoretično gradivo, ki uvaja številne izreke, formule, algoritme itd. Na prvi pogled se morda zdi, da je to precej preprosto. Vendar pa je iskanje vira, v katerem je teorija enotnega državnega izpita iz matematike predstavljena enostavno in razumljivo za študente s katero koli stopnjo izobrazbe, pravzaprav precej težka naloga. Šolskih učbenikov ni vedno pri roki. In iskanje osnovnih formul za izpit iz matematike je lahko težavno tudi na internetu.

Zakaj je tako pomembno študirati teorijo pri matematiki, ne le za tiste, ki opravljajo izpit?

Ker ti širi obzorja. Študij teoretičnega gradiva iz matematike je koristen za vse, ki želijo dobiti odgovore na širok spekter vprašanj, povezanih s spoznavanjem sveta. V naravi je vse urejeno in ima jasno logiko. Prav to se odraža v znanosti, skozi katero je mogoče razumeti svet.
Ker razvija intelekt. Ob študiju referenčnega gradiva za izpit iz matematike, pa tudi pri reševanju različnih problemov, se človek nauči logično razmišljati in sklepati, pravilno in jasno oblikovati misli. Razvija sposobnost analiziranja, posploševanja, sklepanja.

Vabimo vas, da osebno ocenite vse prednosti našega pristopa k sistematizaciji in predstavitvi učnega gradiva.

Matematika se je rodila, ko se je človek zavedal samega sebe in se začel postavljati kot avtonomna enota sveta. Želja po merjenju, primerjanju, izračunavanju tega, kar te obdaja, je tisto, kar je osnova ene od temeljnih znanosti naših dni. Sprva so bili to delci osnovne matematike, ki so omogočali povezovanje števil z njihovimi fizičnimi izrazi, pozneje so sklepe začeli predstavljati le teoretično (zaradi njihove abstraktnosti), a čez nekaj časa, kot je dejal en znanstvenik, " matematika je dosegla zgornjo mejo kompleksnosti, ko so vsa števila." Koncept "kvadratnega korena" se je pojavil v času, ko ga je bilo mogoče zlahka podpreti z empiričnimi podatki, ki presegajo ravnino izračunov.

Kako se je vse začelo

Prva omemba korena, ki je trenutno označena kot √, je bila zabeležena v spisih babilonskih matematikov, ki so postavili temelje sodobne aritmetike. Seveda so bili nekoliko podobni trenutni obliki - znanstveniki tistih let so najprej uporabili velike tablete. Toda v drugem tisočletju pr. e. pripravili so približno formulo za izračun, ki je pokazala, kako vzeti kvadratni koren. Spodnja fotografija prikazuje kamen, na katerem so babilonski znanstveniki vklesali izhodni proces √2, in se je izkazal za tako pravilnega, da je bilo neskladje v odgovoru ugotovljeno šele na deseti decimalki.

Poleg tega je bil koren uporabljen, če je bilo treba najti stranico trikotnika, pod pogojem, da sta bila druga dva znana. No, pri reševanju kvadratnih enačb ni mogoče izogniti ekstrakciji korena.

Poleg babilonskih del je bil predmet članka preučen tudi v kitajskem delu "Matematika v devetih knjigah", stari Grki pa so prišli do zaključka, da vsako število, iz katerega se koren ne izvleče brez ostanka, daje iracionalen rezultat .

Izvor tega izraza je povezan z arabsko predstavitvijo števila: starodavni znanstveniki so verjeli, da kvadrat poljubnega števila raste iz korena, kot rastlina. V latinščini ta beseda zveni kot radix (lahko zasledimo vzorec - vse, kar ima "korensko" pomensko obremenitev, je soglasno, naj bo to redkev ali išias).

Znanstveniki naslednjih generacij so prevzeli to idejo in jo označili kot Rx. Na primer, v 15. stoletju, da bi označili, da je kvadratni koren vzet iz poljubnega števila a, so zapisali R 2 a. "Klopi" √, ki ga poznamo sodobnemu videzu, se je pojavil šele v 17. stoletju po zaslugi Reneja Descartesa.

Naši dnevi

Matematično je kvadratni koren iz y število z, katerega kvadrat je y. Z drugimi besedami, z 2 =y je enakovreden √y=z. Vendar je ta definicija pomembna samo za aritmetični koren, saj implicira nenegativno vrednost izraza. Z drugimi besedami, √y=z, kjer je z večji ali enak 0.

Na splošno, kar velja za določanje algebraičnega korena, je vrednost izraza lahko pozitivna ali negativna. Torej, zaradi dejstva, da je z 2 =y in (-z) 2 =y, imamo: √y=±z ali √y=|z|.

Ker se je ljubezen do matematike z razvojem znanosti samo povečala, obstajajo različni znaki naklonjenosti do nje, ki niso izraženi v suhih izračunih. Na primer, poleg tako zanimivih dogodkov, kot je dan Pi, se praznujejo tudi prazniki kvadratnega korena. Praznujejo se devetkrat v sto letih, določene pa so po naslednjem načelu: številke, ki po vrsti označujejo dan in mesec, morajo biti kvadratni koren leta. Tako bomo naslednjič ta praznik praznovali 4. aprila 2016.

Lastnosti kvadratnega korena na polju R

Skoraj vsi matematični izrazi imajo geometrijsko osnovo, ta usoda ni minila in √y, ki je opredeljena kot stranica kvadrata s površino y.

Kako najti koren števila?

Obstaja več algoritmov za izračun. Najenostavnejši, a hkrati precej okoren, je običajen aritmetični izračun, ki je naslednji:

1) od števila, katerega koren potrebujemo, se po vrsti odštevajo liha števila - dokler ostanek izhoda ni manjši od odštete enote ali celo enak nič. Število premikov bo sčasoma postalo želeno število. Na primer, izračun kvadratnega korena iz 25:

Naslednje liho število je 11, preostanek pa: 1<11. Количество ходов - 5, так что корень из 25 равен 5. Вроде все легко и просто, но представьте, что придется вычислять из 18769?

Za takšne primere obstaja razširitev serije Taylor:

√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , kjer n prevzame vrednosti od 0 do

+∞ in |y|≤1.

Grafični prikaz funkcije z=√y

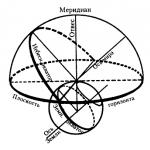
Razmislite o elementarni funkciji z=√y na polju realnih števil R, kjer je y večji ali enak nič. Njen grafikon izgleda takole:

Krivulja raste iz izhodišča in nujno prečka točko (1; 1).

Lastnosti funkcije z=√y na polju realnih števil R

1. Domena definicije obravnavane funkcije je interval od nič do plus neskončnosti (vključena je nič).

2. Obseg vrednosti obravnavane funkcije je interval od nič do plus neskončnost (nič je spet vključena).

3. Funkcija prevzame najmanjšo vrednost (0) samo na točki (0; 0). Najvišje vrednosti ni.

4. Funkcija z=√y ni niti soda niti liha.

5. Funkcija z=√y ni periodična.

6. Obstaja samo ena presečna točka grafa funkcije z=√y s koordinatnimi osemi: (0; 0).

7. Presečišče grafa funkcije z=√y je tudi nič te funkcije.

8. Funkcija z=√y nenehno raste.

9. Funkcija z=√y ima samo pozitivne vrednosti, zato njen graf zaseda prvi koordinatni kot.

Možnosti za prikaz funkcije z=√y

V matematiki se za lažji izračun kompleksnih izrazov včasih uporablja potenčna oblika zapisa kvadratnega korena: √y=y 1/2. Ta možnost je priročna, na primer, pri dvigu funkcije na potencio: (√y) 4 =(y 1/2) 4 =y 2 . Ta metoda je tudi dobra predstavitev za diferenciacijo z integracijo, saj je zaradi nje kvadratni koren predstavljen z navadno močnostno funkcijo.

In pri programiranju je zamenjava za simbol √ kombinacija črk sqrt.

Omeniti velja, da je na tem področju kvadratni koren v velikem povpraševanju, saj je del večine geometrijskih formul, potrebnih za izračune. Sam algoritem štetja je precej zapleten in temelji na rekurziji (funkcija, ki kliče samo sebe).

Kvadratni koren v kompleksnem polju C

Na splošno je bil predmet tega članka, ki je spodbudil odkritje polja kompleksnih števil C, saj je matematike preganjalo vprašanje pridobivanja korena sode stopnje iz negativnega števila. Tako se je pojavila imaginarna enota i, za katero je značilna zelo zanimiva lastnost: njen kvadrat je -1. Zahvaljujoč temu so kvadratne enačbe in z negativnim diskriminantom dobili rešitev. V C so za kvadratni koren pomembne enake lastnosti kot v R, edina stvar je, da so odstranjene omejitve korenskega izraza.