Pagrindinės elementarios funkcijos ir jų savybės. Pagrindinės funkcijų savybės

Visas pagrindinių elementarių funkcijų sąrašas

Į pagrindinių elementarių funkcijų klasę įeina:

1. Pastovi funkcija $y=C$, kur $C$ yra konstanta. Tokia funkcija įgauna tą pačią reikšmę $C$ bet kuriam $x$.
2. Laipsnio funkcija $y=x^(a) $, kur eksponentas $a$ yra realusis skaičius.
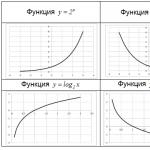
3. Eksponentinė funkcija $y=a^(x) $, kur bazė yra $a>0$, $a\ne 1$ laipsnis.
4. Logaritminė funkcija $y=\log _(a) x$, kur logaritmo bazė yra $a>0$, $a\ne 1$.
5. Trigonometrinės funkcijos $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ sek.\,x$.
6. Atvirkštinės trigonometrinės funkcijos $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , x$.

Maitinimo funkcijos

Apsvarstysime laipsnio funkcijos $y=x^(a) $ elgseną tais pačiais paprasčiausiais atvejais, kai jos rodiklis lemia sveikojo skaičiaus didinimą ir šaknies ištraukimą.

1 atvejis

Funkcijos $y=x^(a) $ eksponentas yra natūralusis skaičius, tai yra $y=x^(n) $, $n\in N$.

Jei $n=2\cdot k$ yra lyginis skaičius, tai funkcija $y=x^(2\cdot k) $ yra lyginė ir didėja neribotai, tarsi argumentas $\left(x\to +\infty \ right )$, o su jo neribotu mažėjimu $\left(x\to -\infty \right)$. Tokį funkcijos elgesį galima apibūdinti išraiškomis $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ ir $\mathop(\lim )\ limits_(x\to -\infty ) x^(2\cdot k) =+\infty $, o tai reiškia, kad funkcija abiem atvejais didėja be apribojimų ($\lim $ yra riba). Pavyzdys: funkcijos $y=x^(2) $ grafikas.

Jei $n=2\cdot k-1$ yra nelyginis skaičius, tai funkcija $y=x^(2\cdot k-1) $ yra nelyginė, didėja neribotai, kai argumentas didėja neribotai, ir mažėja neribotai, kai jis mažėja neribotam laikui. Tokį funkcijos elgesį galima apibūdinti išraiškomis $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ ir $\mathop(\lim )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. Pavyzdys: funkcijos $y=x^(3) $ grafikas.

2 atvejis

Funkcijos $y=x^(a) $ eksponentas yra neigiamas sveikasis skaičius, tai yra $y=\frac(1)(x^(n) ) $, $n\in N$.

Jei $n=2\cdot k$ yra lyginis skaičius, tai funkcija $y=\frac(1)(x^(2\cdot k) ) $ yra lyginė ir asimptotiškai (palaipsniui) artėja prie nulio, kaip ir neriboto didinimo argumento atveju , ir su neribotu jo mažėjimu. Tokį funkcijos elgesį galima apibūdinti viena išraiška $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$, o tai reiškia, kad neribotai padidėjus argumentui absoliučia verte, funkcijos riba lygi nuliui. Be to, kadangi argumentas linkęs į nulį tiek kairėje $\left(x\to 0-0\right)$, tiek dešinėje $\left(x\to 0+0\right)$, funkcija didėja be riba. Todėl išraiškos $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ ir $\mathop(\lim )\ limitai_ galioja (x\iki 0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, o tai reiškia, kad funkcija $y=\frac(1)(x^(2) \cdot k ) ) $ abiem atvejais turi begalinę ribą, lygią $+\infty $. Pavyzdys: funkcijos $y=\frac(1)(x^(2) ) $ grafikas.

Jei $n=2\cdot k-1$ yra nelyginis skaičius, tai funkcija $y=\frac(1)(x^(2\cdot k-1) ) $ yra nelyginė ir asimptotiškai artėja prie nulio, tarsi abu argumentas didėja, o kai mažėja neribotai. Tokį funkcijos elgesį galima apibūdinti viena išraiška $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$. Be to, argumentui artėjant prie nulio kairėje, funkcija mažėja be apribojimų, o argumentui artėjant prie nulio dešinėje, funkcija didėja be apribojimų, tai yra $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ ir $\mathop(\lim )\limits_(x\to 0+0) \frac(1)( x^(2\cdot k-1) ) =+\infty $. Pavyzdys: funkcijos $y=\frac(1)(x) $ grafikas.

3 atvejis

Funkcijos $y=x^(a) $ eksponentas yra atvirkštinis natūralusis skaičius, tai yra $y=\sqrt[(n)](x) $, $n\in N$.

Jei $n=2\cdot k$ yra lyginis skaičius, tai funkcija $y=\pm \sqrt[(2\cdot k)](x) $ yra dviejų reikšmių ir apibrėžiama tik $x\ge 0 $. Neribotai padidinus argumentą, funkcijos $y=+\sqrt[(2\cdot k)](x) $ reikšmė neribotai didėja, o funkcijos $y=-\sqrt[(2\) cdot k)](x) $ mažėja neribotai , tai yra $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right )=+\infty $ ir $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. Pavyzdys: funkcijos $y=\pm \sqrt(x) $ grafikas.

Jei $n=2\cdot k-1$ yra nelyginis skaičius, tai funkcija $y=\sqrt[(2\cdot k-1)](x) $ yra nelyginė, didėja neribotai neribotai didėjant argumentui ir mažėja neribotai, kai neribota, tai mažėja, tai yra $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ ir $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. Pavyzdys: funkcijos $y=\sqrt[(3)](x) $ grafikas.

Eksponentinės ir logaritminės funkcijos

Eksponentinės $y=a^(x) $ ir logaritminės $y=\log _(a) x$ funkcijos yra atvirkštinės. Jų grafikai yra simetriški pirmosios ir trečiosios koordinačių kampų bendrosios pusiausvyros atžvilgiu.

Kai argumentas $\left(x\to +\infty \right)$ didėja neribotą laiką, eksponentinė funkcija arba $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ didėja neribotą laiką, jei $a>1$ arba asimptotiškai artėja prie nulio $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =0$, jei $a1$ arba $\mathop didėja be apribojimų (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, jei $a

Funkcijos $y=a^(x) $ būdinga reikšmė yra $x=0$. Šiuo atveju visos eksponentinės funkcijos, nepaisant $a$, būtinai susikerta su $Oy$ ašimi ties $y=1$. Pavyzdžiai: funkcijų $y=2^(x) $ ir $y = \left (\frac(1)(2) \right)^(x) $ grafikai.

Logaritminė funkcija $y=\log _(a) x$ apibrėžiama tik $x > 0$.

Kai argumentas $\left(x\to +\infty \right)$ didėja neribotą laiką, logaritminė funkcija arba $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+ \ neribotą laiką didėja infty $, jei $a>1$ arba mažėja be apribojimų $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, jei $a1 $ arba be apribojimo $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $ padidėja, jei $a

Funkcijos $y=\log _(a) x$ būdinga reikšmė yra $y=0$. Šiuo atveju visos logaritminės funkcijos, nepaisant $a$, būtinai susikerta su $Ox$ ašimi ties $x=1$. Pavyzdžiai: funkcijų $y=\log _(2) x$ ir $y=\log _(1/2) x$ grafikai.

Kai kurios logaritminės funkcijos turi specialų žymėjimą. Visų pirma, jei logaritmo bazė yra $a=10$, tai toks logaritmas vadinamas dešimtainiu, o atitinkama funkcija rašoma kaip $y=\lg x$. O jei logaritmo pagrindu pasirenkamas iracionalusis skaičius $e=2,7182818\ldots $, tai toks logaritmas vadinamas natūraliuoju, o atitinkama funkcija rašoma $y=\ln x$. Jo atvirkštinė reikšmė yra funkcija $y=e^(x) $, vadinama eksponentu.

Pagrindinės elementarios funkcijos yra: pastovi funkcija (konstanta), šaknis n laipsnis, laipsnio funkcija, eksponentinė, logaritminė funkcija, trigonometrinės ir atvirkštinės trigonometrinės funkcijos.

Nuolatinė funkcija.

Pastovi funkcija visų realiųjų skaičių aibėje pateikiama pagal formulę , kur C– kažkoks tikrasis skaičius. Pastovi funkcija priskiria kiekvieną faktinę nepriklausomo kintamojo reikšmę x ta pati priklausomo kintamojo reikšmė y- prasmė SU. Pastovi funkcija taip pat vadinama konstanta.

Pastovios funkcijos grafikas yra tiesė, lygiagreti x ašiai ir einanti per tašką su koordinatėmis (0,C). Pavyzdžiui, parodykime pastovių funkcijų grafikus y = 5,y=-2 ir , kurios žemiau esančiame paveikslėlyje atitinka atitinkamai juodą, raudoną ir mėlyną linijas.

Pastovios funkcijos savybės.

Domenas: visas realiųjų skaičių rinkinys.

Nuolatinė funkcija yra lygi.

Reikšmių diapazonas: rinkinys, susidedantis iš vienaskaitos skaičiaus SU.

Pastovi funkcija yra nedidėjanti ir nemažėjanti (todėl ji yra pastovi).

Nėra prasmės kalbėti apie konstantos išgaubimą ir įgaubimą.

Asimptotų nėra.

Funkcija eina per tašką (0,C) koordinačių plokštuma.

n-oji šaknis.

Panagrinėkime pagrindinę elementariąją funkciją, kurią pateikia formulė, kur n– natūralusis skaičius, didesnis už vienetą.

N-oji šaknis, n yra lyginis skaičius.

Pradėkime nuo šaknies funkcijos n-toji šaknies eksponento lygiųjų verčių galia n.

Pavyzdžiui, čia yra paveikslėlis su funkcijų grafikų vaizdais ir , jie atitinka juodas, raudonas ir mėlynas linijas.

Lyginio laipsnio šaknies funkcijų grafikai turi panašią išvaizdą kitoms eksponento reikšmėms.

Šakninės funkcijos savybėsn -th galia netn .

N-oji šaknis, n yra nelyginis skaičius.

Šaknies funkcija n-oji galia su nelyginiu šaknies rodikliu n yra apibrėžtas visoje realiųjų skaičių aibėje. Pavyzdžiui, čia yra funkcijų grafikai ir , jie atitinka juodas, raudonas ir mėlynas kreives.

1) Funkcijų sritis ir funkcijų diapazonas.

Funkcijos domenas yra visų galiojančių argumentų reikšmių rinkinys x(kintamasis x), kuriai skirta funkcija y = f(x) Atkaklus. Funkcijos diapazonas yra visų realių reikšmių rinkinys y, kurią funkcija priima.

Elementariojoje matematikoje funkcijos tiriamos tik realiųjų skaičių aibėje.

2) Funkcijos nuliai.

Funkcijos nulis yra argumento, kuriame funkcijos reikšmė lygi nuliui, reikšmė.

3) Funkcijos pastovaus ženklo intervalai.

Funkcijos pastovaus ženklo intervalai yra argumentų reikšmių rinkiniai, kurių funkcijos reikšmės yra tik teigiamos arba tik neigiamos.

4) Funkcijos monotoniškumas.

Didėjanti funkcija (tam tikrame intervale) yra funkcija, kurioje didesnė argumento reikšmė iš šio intervalo atitinka didesnę funkcijos reikšmę.

Mažėjanti funkcija (tam tikrame intervale) yra funkcija, kurioje didesnė argumento reikšmė iš šio intervalo atitinka mažesnę funkcijos reikšmę.

5) Lyginė (nelyginė) funkcija.

Lyginė funkcija yra funkcija, kurios apibrėžimo sritis yra simetriška kilmės atžvilgiu ir bet kuriai X iš apibrėžimo srities lygybė f(-x) = f(x). Lyginės funkcijos grafikas yra simetriškas ordinatės atžvilgiu.

Nelyginė funkcija yra funkcija, kurios apibrėžimo sritis yra simetriška kilmės atžvilgiu ir bet kuriai X iš apibrėžimo srities lygybė yra teisinga f(-x) = - f(x). Nelyginės funkcijos grafikas yra simetriškas kilmei.

6) Ribotos ir neribotos funkcijos.

Funkcija vadinama ribota, jei yra teigiamas skaičius M, kad |f(x)| ≤ M visoms x reikšmėms. Jei tokio skaičiaus nėra, tada funkcija yra neribota.

7) Funkcijos periodiškumas.

Funkcija f(x) yra periodinė, jei yra nulinis skaičius T, kad bet kuriam x iš funkcijos apibrėžimo srities galioja: f(x+T) = f(x). Šis mažiausias skaičius vadinamas funkcijos periodu. Visos trigonometrinės funkcijos yra periodinės. (Trigonometrinės formulės).

19. Pagrindinės elementarios funkcijos, jų savybės ir grafikai. Funkcijų taikymas ekonomikoje.

Pagrindinės elementarios funkcijos. Jų savybės ir grafikai

1. Tiesinė funkcija.

Linijinė funkcija vadinama formos funkcija, kur x yra kintamasis, a ir b yra realieji skaičiai.

Skaičius A vadinamas tiesės nuolydžiu, jis lygus šios tiesės polinkio kampo į teigiamą abscisių ašies kryptį liestine. Tiesinės funkcijos grafikas yra tiesi linija. Jis apibrėžiamas dviem taškais.

Tiesinės funkcijos savybės

1. Apibrėžimo sritis – visų realiųjų skaičių aibė: D(y)=R

2. Reikšmių aibė yra visų realiųjų skaičių aibė: E(y)=R

3. Funkcija įgyja nulinę reikšmę, kai arba.

4. Funkcija didėja (mažėja) visoje apibrėžimo srityje.

5. Tiesinė funkcija yra ištisinė visoje apibrėžimo srityje, diferencijuota ir .

2. Kvadratinė funkcija.

Formos funkcija, kur x yra kintamasis, koeficientai a, b, c yra realieji skaičiai, vadinama kvadratinis

Atsižvelgdamas į sudėtingo kintamojo funkcijas, Liouville'is elementarias funkcijas apibrėžė kiek plačiau. Elementari funkcija y kintamasis x- analitinė funkcija, kurią galima pavaizduoti kaip algebrinę funkciją x ir funkcijas , ir yra tam tikros algebrinės funkcijos logaritmas arba eksponentas g 1 nuo x .

Pavyzdžiui, nuodėmė ( x) – algebrinė funkcija e ix .

Neribodami svarstymo bendrumo, funkcijas galime laikyti algebriškai nepriklausomomis, tai yra, jei algebrinė lygtis tenkinama visoms x, tada visi daugianario koeficientai yra lygūs nuliui.

Elementariųjų funkcijų diferencijavimas

Kur z 1 "(z) lygus arba g 1 " / g 1 arba z 1 g 1" priklausomai nuo to, ar tai logaritmas z 1 arba eksponentinis ir tt Praktikoje patogu naudoti išvestinę lentelę.

Elementariųjų funkcijų integravimas

Liouville'io teorema yra pagrindas kurti elementariųjų funkcijų simbolinės integracijos algoritmus, įgyvendintus, pvz.

Ribų skaičiavimas

Liouville'io teorija netaikoma skaičiuojant ribas. Nežinia, ar yra algoritmas, kuris, pateikęs elementariąja formule pateiktą seką, duoda atsakymą, ar ji turi ribą, ar ne. Pavyzdžiui, atviras klausimas, ar seka susilieja.

Literatūra

• J. Liouville. Mémoire sur l'integration d'une classe de fonctions transcendantes// J. Reine Angew. Matematika. Bd. 13, p. 93-118. (1835 m.)
• J.F. Ritt. Integracija baigtinėmis sąlygomis. N.-Y., 1949 // http://lib.homelinux.org
• A. G. Chovanskis. Topologinė Galois teorija: baigtinės formos lygčių išsprendžiamumas ir neišsprendžiamumas Ch. 1. M, 2007 m

Pastabos

Wikimedia fondas. 2010 m.

• Elementarus sužadinimas
• Elementarus rezultatas

Pažiūrėkite, kas yra „pagrindinė funkcija“ kituose žodynuose:

elementari funkcija- Funkcija, kuri, padalyta į mažesnes funkcijas, negali būti vienareikšmiškai apibrėžta skaitmeninėje perdavimo hierarchijoje. Todėl tinklo požiūriu jis yra nedalomas (ITU T G.806). Temos: telekomunikacijos, pagrindinės sąvokos EN pritaikymo funkcijaA... Techninis vertėjo vadovas

sąveikos tarp tinklo lygių funkcija- Elementari funkcija, užtikrinanti būdingos informacijos sąveiką tarp dviejų tinklo sluoksnių. (ITU T G.806). Temos: telekomunikacijos, pagrindinės EN lygmens sąvokos... ... Techninis vertėjo vadovas