बुनियादी प्राथमिक कार्य और उनके गुण। कार्यों के मूल गुण

बुनियादी प्राथमिक कार्यों की पूरी सूची

बुनियादी प्रारंभिक कार्यों के वर्ग में निम्नलिखित शामिल हैं:

1. स्थिर फलन $y=C$, जहां $C$ एक स्थिरांक है। ऐसा फ़ंक्शन किसी भी $x$ के लिए समान मान $C$ लेता है।
2. पावर फ़ंक्शन $y=x^(a) $, जहां घातांक $a$ एक वास्तविक संख्या है।
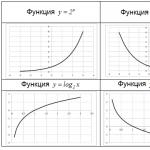
3. घातीय फ़ंक्शन $y=a^(x) $, जहां आधार डिग्री $a>0$, $a\ne 1$ है।
4. लघुगणक फ़ंक्शन $y=\log _(a) x$, जहां लघुगणक का आधार $a>0$, $a\ne 1$ है।
5. त्रिकोणमितीय फलन $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ सेकंड\,x$.
6. व्युत्क्रम त्रिकोणमितीय फलन $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , एक्स$.

शक्ति कार्य

हम उन सरलतम मामलों के लिए पावर फ़ंक्शन $y=x^(a) $ के व्यवहार पर विचार करेंगे जब इसका घातांक पूर्णांक घातांक और मूल निष्कर्षण निर्धारित करता है।

मामला एक

फ़ंक्शन $y=x^(a) $ का घातांक एक प्राकृतिक संख्या है, अर्थात, $y=x^(n) $, $n\in N$।

यदि $n=2\cdot k$ एक सम संख्या है, तो फ़ंक्शन $y=x^(2\cdot k) $ सम है और अनिश्चित काल तक बढ़ता है जैसे कि तर्क $\left(x\to +\infty \right) )$, और इसकी असीमित कमी के साथ $\left(x\to -\infty \right)$. फ़ंक्शन के इस व्यवहार को अभिव्यक्ति $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ और $\mathop(\lim )\ द्वारा वर्णित किया जा सकता है सीमा_(x\to -\infty ) x^(2\cdot k) =+\infty $, जिसका अर्थ है कि दोनों मामलों में फ़ंक्शन बिना सीमा के बढ़ता है ($\lim $ सीमा है)। उदाहरण: फ़ंक्शन का ग्राफ़ $y=x^(2) $।

यदि $n=2\cdot k-1$ एक विषम संख्या है, तो फ़ंक्शन $y=x^(2\cdot k-1) $ विषम है, जैसे-जैसे तर्क अनिश्चित काल तक बढ़ता है, अनिश्चित काल तक बढ़ता है, और तर्क के रूप में अनिश्चित काल तक घटता है अनिश्चित काल तक घटता है. फ़ंक्शन के इस व्यवहार को अभिव्यक्ति $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ और $\mathop(\lim) द्वारा वर्णित किया जा सकता है )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. उदाहरण: फ़ंक्शन का ग्राफ़ $y=x^(3) $.

केस 2

फ़ंक्शन $y=x^(a) $ का घातांक एक नकारात्मक पूर्णांक है, अर्थात, $y=\frac(1)(x^(n) ) $, $n\in N$।

यदि $n=2\cdot k$ एक सम संख्या है, तो फ़ंक्शन $y=\frac(1)(x^(2\cdot k) ) $ सम है और असीमित वृद्धि तर्क के साथ स्पर्शोन्मुख रूप से (धीरे-धीरे) शून्य के करीब पहुंचता है , और इसकी असीमित कमी के साथ। फ़ंक्शन के इस व्यवहार को एकल अभिव्यक्ति $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$ द्वारा वर्णित किया जा सकता है, जिसका अर्थ है कि निरपेक्ष मान में तर्क में असीमित वृद्धि के साथ, फ़ंक्शन की सीमा शून्य है। इसके अलावा, जैसे-जैसे तर्क बाईं ओर $\left(x\to 0-0\right)$ और दाईं ओर $\left(x\to 0+0\right)$ दोनों पर शून्य हो जाता है, फ़ंक्शन बिना बढ़े बढ़ता है सीमा. इसलिए, अभिव्यक्ति $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ और $\mathop(\lim )\ सीमाएँ_ मान्य हैं (x\to 0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, जिसका अर्थ है कि फ़ंक्शन $y=\frac(1)(x^(2) \cdot k ) ) दोनों ही मामलों में $ की अनंत सीमा $+\infty $ के बराबर होती है। उदाहरण: फ़ंक्शन का ग्राफ़ $y=\frac(1)(x^(2) ) $.

यदि $n=2\cdot k-1$ एक विषम संख्या है, तो फ़ंक्शन $y=\frac(1)(x^(2\cdot k-1) ) $ विषम है और स्पर्शोन्मुख रूप से शून्य के करीब पहुंचता है जैसे कि दोनों जब तर्क कब बढ़ता है और कब घटता है, इसकी कोई सीमा नहीं है। फ़ंक्शन के इस व्यवहार को एकल अभिव्यक्ति $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$ द्वारा वर्णित किया जा सकता है। इसके अलावा, जैसे-जैसे तर्क बाईं ओर शून्य के करीब पहुंचता है, फ़ंक्शन बिना किसी सीमा के घटता जाता है, और जैसे-जैसे तर्क दाईं ओर शून्य के करीब पहुंचता है, फ़ंक्शन बिना किसी सीमा के बढ़ता है, यानी, $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ और $\mathop(\lim )\limits_(x\to 0+0) \frac(1)( x^(2\cdot k-1) ) =+\infty $. उदाहरण: फ़ंक्शन का ग्राफ $y=\frac(1)(x) $.

केस 3

फ़ंक्शन $y=x^(a) $ का घातांक प्राकृतिक संख्या का व्युत्क्रम है, अर्थात, $y=\sqrt[(n)](x) $, $n\in N$।

यदि $n=2\cdot k$ एक सम संख्या है, तो फ़ंक्शन $y=\pm \sqrt[(2\cdot k)](x) $ दो-मूल्य वाला है और केवल $x\ge 0 के लिए परिभाषित है $. तर्क में असीमित वृद्धि के साथ, फ़ंक्शन का मान $y=+\sqrt[(2\cdot k)](x) $ असीमित रूप से बढ़ता है, और फ़ंक्शन का मान $y=-\sqrt[(2\) cdot k)](x) $ असीमित रूप से घटता है, अर्थात, $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right )=+\infty $ और $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. उदाहरण: फ़ंक्शन का ग्राफ़ $y=\pm \sqrt(x) $।

यदि $n=2\cdot k-1$ एक विषम संख्या है, तो फ़ंक्शन $y=\sqrt[(2\cdot k-1)](x) $ विषम है, तर्क में असीमित वृद्धि के साथ असीमित रूप से बढ़ता है और असीमित होने पर असीमित रूप से घटता है, यह घटता है, अर्थात, $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ और $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. उदाहरण: फ़ंक्शन का ग्राफ़ $y=\sqrt[(3)](x) $.

घातांकीय और लघुगणकीय कार्य

घातांक $y=a^(x) $ और लघुगणक $y=\log _(a) x$ फ़ंक्शन परस्पर व्युत्क्रम हैं। उनके ग्राफ़ पहले और तीसरे निर्देशांक कोणों के उभयनिष्ठ समद्विभाजक के संबंध में सममित हैं।

जब तर्क $\left(x\to +\infty \right)$ अनिश्चित काल तक बढ़ता है, तो घातीय फ़ंक्शन या $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ अनिश्चित काल तक बढ़ता है, यदि $a>1$, या असममित रूप से शून्य के करीब पहुंचता है $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =0$, यदि $a1$, या $\mathop बिना किसी सीमा के बढ़ता है (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, यदि $a

फ़ंक्शन $y=a^(x) $ के लिए विशिष्ट मान $x=0$ है। इस मामले में, सभी घातीय फ़ंक्शन, $a$ की परवाह किए बिना, आवश्यक रूप से $Oy$ अक्ष को $y=1$ पर काटते हैं। उदाहरण: फ़ंक्शन के ग्राफ़ $y=2^(x) $ और $y = \left (\frac(1)(2) \right)^(x) $.

लॉगरिदमिक फ़ंक्शन $y=\log _(a) x$ केवल $x > 0$ के लिए परिभाषित किया गया है।

जैसे-जैसे तर्क $\left(x\to +\infty \right)$ अनिश्चित काल तक बढ़ता है, लघुगणकीय फ़ंक्शन या $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+ \ अनिश्चित काल तक $ बढ़ाता है, यदि $a>1$, या बिना किसी सीमा के घटता है $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, यदि $a1 $, या बिना सीमा के $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $ बढ़ता है यदि $a

फ़ंक्शन $y=\log _(a) x$ के लिए विशिष्ट मान $y=0$ है। इस मामले में, सभी लघुगणकीय फ़ंक्शन, $a$ की परवाह किए बिना, आवश्यक रूप से $Ox$ अक्ष को $x=1$ पर काटते हैं। उदाहरण: फ़ंक्शन $y=\log _(2) x$ और $y=\log _(1/2) x$ के ग्राफ़।

कुछ लघुगणकीय कार्यों में विशेष अंकन होता है। विशेष रूप से, यदि लघुगणक का आधार $a=10$ है, तो ऐसे लघुगणक को दशमलव कहा जाता है, और संबंधित फ़ंक्शन को $y=\lg x$ के रूप में लिखा जाता है। और यदि अपरिमेय संख्या $e=2.7182818\ldots $ को लघुगणक के आधार के रूप में चुना जाता है, तो ऐसे लघुगणक को प्राकृतिक कहा जाता है, और संबंधित फ़ंक्शन को $y=\ln x$ के रूप में लिखा जाता है। इसका व्युत्क्रम फ़ंक्शन $y=e^(x) $ है, जिसे घातांक कहा जाता है।

बुनियादी प्राथमिक कार्यहैं: स्थिर कार्य (स्थिर), जड़ एन-वीं डिग्री, पावर फ़ंक्शन, घातांक, लॉगरिदमिक फ़ंक्शन, त्रिकोणमितीय और व्युत्क्रम त्रिकोणमितीय फ़ंक्शन।

स्थायी कार्य.

सूत्र द्वारा सभी वास्तविक संख्याओं के समुच्चय पर एक स्थिर फलन दिया जाता है, जहाँ सी– कुछ वास्तविक संख्या. एक स्थिर फ़ंक्शन स्वतंत्र चर के प्रत्येक वास्तविक मान को निर्दिष्ट करता है एक्सआश्रित चर का समान मान य- अर्थ साथ. एक स्थिर फलन को स्थिरांक भी कहा जाता है।

एक स्थिर फलन का ग्राफ x-अक्ष के समानांतर और निर्देशांक वाले बिंदु से गुजरने वाली एक सीधी रेखा है (0,सी). उदाहरण के लिए, आइए स्थिर फलनों के ग्राफ़ दिखाएं y=5,y=-2और, जो नीचे दिए गए चित्र में क्रमशः काली, लाल और नीली रेखाओं के अनुरूप है।

एक स्थिर फलन के गुण.

डोमेन: वास्तविक संख्याओं का संपूर्ण सेट.

अचर फलन सम है.

मानों की सीमा: एक एकल संख्या से युक्त सेट साथ.

एक स्थिर फलन न तो बढ़ता है और न ही घटता है (इसीलिए यह स्थिर है)।

किसी स्थिरांक की उत्तलता और अवतलता के बारे में बात करने का कोई मतलब नहीं है।

कोई स्पर्शोन्मुख नहीं हैं.

फ़ंक्शन बिंदु से होकर गुजरता है (0,सी)विमान का समन्वय।

nवीं डिग्री की जड़.

आइए मूल प्राथमिक फ़ंक्शन पर विचार करें, जो सूत्र द्वारा दिया गया है, जहां एन- एक से बड़ी प्राकृतिक संख्या।

nवाँ मूल, n एक सम संख्या है।

आइए रूट फ़ंक्शन से शुरू करें एनमूल घातांक के सम मानों के लिए -वीं शक्ति एन.

उदाहरण के तौर पर, यहां फ़ंक्शन ग्राफ़ की छवियों वाला एक चित्र है और, वे काली, लाल और नीली रेखाओं के अनुरूप हैं।

सम-डिग्री रूट फ़ंक्शंस के ग्राफ़ में घातांक के अन्य मानों के लिए समान उपस्थिति होती है।

रूट फ़ंक्शन के गुणएन -सम के लिए शक्तिएन .

nवाँ मूल, n एक विषम संख्या है।

मूल कार्य एनएक विषम मूल घातांक के साथ -वीं शक्ति एनवास्तविक संख्याओं के संपूर्ण सेट पर परिभाषित किया गया है। उदाहरण के लिए, यहां फ़ंक्शन ग्राफ़ हैं और, वे काले, लाल और नीले वक्रों के अनुरूप हैं।

1) फ़ंक्शन डोमेन और फ़ंक्शन रेंज.

किसी फ़ंक्शन का डोमेन सभी वैध मान्य तर्क मानों का सेट है एक्स(चर एक्स), जिसके लिए फ़ंक्शन वाई = एफ(एक्स)दृढ़ निश्चय वाला। किसी फ़ंक्शन की सीमा सभी वास्तविक मानों का समुच्चय है य, जिसे फ़ंक्शन स्वीकार करता है।

प्रारंभिक गणित में, कार्यों का अध्ययन केवल वास्तविक संख्याओं के सेट पर किया जाता है।

2) फ़ंक्शन शून्य.

फ़ंक्शन शून्य उस तर्क का मान है जिस पर फ़ंक्शन का मान शून्य के बराबर होता है।

3) किसी फ़ंक्शन के स्थिर चिह्न का अंतराल.

किसी फ़ंक्शन के स्थिर चिह्न के अंतराल तर्क मानों के सेट होते हैं जिन पर फ़ंक्शन मान केवल सकारात्मक या केवल नकारात्मक होते हैं।

4) फ़ंक्शन की एकरसता.

एक बढ़ता हुआ फ़ंक्शन (एक निश्चित अंतराल में) एक ऐसा फ़ंक्शन होता है जिसमें इस अंतराल से तर्क का बड़ा मान फ़ंक्शन के बड़े मान से मेल खाता है।

एक घटता हुआ फ़ंक्शन (एक निश्चित अंतराल में) एक ऐसा फ़ंक्शन होता है जिसमें इस अंतराल से तर्क का बड़ा मान फ़ंक्शन के छोटे मान से मेल खाता है।

5) सम (विषम) फ़ंक्शन.

एक सम फलन एक ऐसा फलन है जिसकी परिभाषा का क्षेत्र मूल और किसी के संबंध में सममित है एक्सपरिभाषा के क्षेत्र से समानता एफ(-एक्स) = एफ(एक्स). एक सम फलन का ग्राफ कोटि के प्रति सममित होता है।

एक विषम फलन एक ऐसा फलन है जिसकी परिभाषा का क्षेत्र मूल और किसी के संबंध में सममित है एक्सपरिभाषा के क्षेत्र से समानता सत्य है एफ(-एक्स) = - एफ(एक्स). एक विषम फलन का ग्राफ मूल बिन्दु के प्रति सममित होता है।

6) सीमित एवं असीमित कार्य.

यदि कोई धनात्मक संख्या M ऐसी हो कि |f(x)| तो किसी फ़ंक्शन को परिबद्ध कहा जाता है ≤ x के सभी मानों के लिए M. यदि ऐसी कोई संख्या मौजूद नहीं है, तो फ़ंक्शन असीमित है।

7) समारोह की आवधिकता.

एक फ़ंक्शन f(x) आवधिक है यदि इसमें एक गैर-शून्य संख्या T है जैसे कि फ़ंक्शन की परिभाषा के डोमेन से किसी भी x के लिए निम्नलिखित है: f(x+T) = f(x)। इस सबसे छोटी संख्या को फलन का आवर्त कहा जाता है। सभी त्रिकोणमितीय फलन आवर्ती होते हैं। (त्रिकोणमितीय सूत्र).

19. बुनियादी प्राथमिक कार्य, उनके गुण और ग्राफ़। अर्थशास्त्र में कार्यों का अनुप्रयोग.

बुनियादी प्राथमिक कार्य. उनके गुण और ग्राफ़

1. रैखिक कार्य.

रैखिक प्रकार्य फॉर्म का एक फ़ंक्शन कहा जाता है, जहां x एक चर है, a और b वास्तविक संख्याएं हैं।

संख्या एइसे रेखा का ढलान कहा जाता है, यह x-अक्ष की धनात्मक दिशा पर इस रेखा के झुकाव कोण की स्पर्शरेखा के बराबर है। एक रैखिक फलन का ग्राफ़ एक सीधी रेखा है। इसे दो बिंदुओं द्वारा परिभाषित किया गया है।

एक रैखिक फलन के गुण

1. परिभाषा का क्षेत्र - सभी वास्तविक संख्याओं का समुच्चय: D(y)=R

2. मानों का समुच्चय सभी वास्तविक संख्याओं का समुच्चय है: E(y)=R

3. फ़ंक्शन शून्य मान लेता है जब या।

4. परिभाषा के संपूर्ण क्षेत्र में फ़ंक्शन बढ़ता (घटता) है।

5. एक रैखिक फलन परिभाषा के संपूर्ण क्षेत्र में निरंतर होता है, अवकलनीय और।

2. द्विघात फलन.

प्रपत्र का एक फ़ंक्शन, जहां x एक चर है, गुणांक a, b, c वास्तविक संख्याएं हैं, कहलाता है द्विघात

एक जटिल चर के कार्यों पर विचार करते हुए, लिउविले ने प्राथमिक कार्यों को कुछ अधिक व्यापक रूप से परिभाषित किया। प्राथमिक कार्य यचर एक्स- विश्लेषणात्मक फ़ंक्शन, जिसे बीजगणितीय फ़ंक्शन के रूप में दर्शाया जा सकता है एक्सऔर कार्य , और कुछ बीजीय फलन का लघुगणक या घातांक है जी 1 से एक्स .

उदाहरण के लिए, पाप( एक्स) - का बीजगणितीय कार्य इ मैंएक्स .

विचार की व्यापकता को सीमित किए बिना, हम कार्यों को बीजगणितीय रूप से स्वतंत्र मान सकते हैं, अर्थात, यदि बीजगणितीय समीकरण सभी के लिए संतुष्ट है एक्स, तो बहुपद के सभी गुणांक शून्य के बराबर हैं.

प्राथमिक कार्यों का विभेदन

कहाँ जेड 1 "(जेड) बराबर या जी 1 " / जी 1 या जेड 1 जी 1" इस पर निर्भर करता है कि यह एक लघुगणक है या नहीं जेड 1 या घातांक, आदि। व्यवहार में, व्युत्पन्न तालिका का उपयोग करना सुविधाजनक है।

प्राथमिक कार्यों को एकीकृत करना

लिउविले का प्रमेय प्राथमिक कार्यों के प्रतीकात्मक एकीकरण के लिए एल्गोरिदम बनाने का आधार है, उदाहरण के लिए, में लागू किया गया

सीमा की गणना

लिउविले का सिद्धांत सीमाओं की गणना पर लागू नहीं होता है। यह ज्ञात नहीं है कि क्या कोई एल्गोरिदम है, जो प्राथमिक सूत्र द्वारा दिए गए अनुक्रम को देखते हुए उत्तर देता है कि इसकी कोई सीमा है या नहीं। उदाहरण के लिए, यह प्रश्न खुला है कि क्या अनुक्रम अभिसरित होता है।

साहित्य

• जे. लिउविल. कार्यों के एकीकरण के एक अन्य वर्ग का संस्मरण// जे. रेइन एंज्यू। गणित। बी.डी. 13, पृ. 93-118. (1835)
• जे.एफ. रिट. सीमित शर्तों में एकीकरण. एन.-वाई., 1949 // http://lib.homelinux.org
• ए जी खोवांस्की। टोपोलॉजिकल गैलोइस सिद्धांत: परिमित रूप में समीकरणों की सॉल्वैबिलिटी और अनसॉल्वैबिलिटीचौ. 1. एम, 2007

टिप्पणियाँ

विकिमीडिया फाउंडेशन. 2010.

• प्राथमिक उत्तेजना
• प्राथमिक परिणाम

देखें अन्य शब्दकोशों में "प्राथमिक कार्य" क्या है:

प्राथमिक कार्य- एक फ़ंक्शन, जिसे यदि छोटे फ़ंक्शंस में विभाजित किया जाता है, तो डिजिटल ट्रांसमिशन पदानुक्रम में विशिष्ट रूप से परिभाषित नहीं किया जा सकता है। इसलिए, नेटवर्क के दृष्टिकोण से यह अविभाज्य है (आईटीयू टी जी.806)। विषय: दूरसंचार, बुनियादी अवधारणाएँ EN अनुकूलन फ़ंक्शनए... तकनीकी अनुवादक की मार्गदर्शिका

नेटवर्क स्तरों के बीच अंतःक्रिया का कार्य- एक प्राथमिक कार्य जो दो नेटवर्क परतों के बीच विशिष्ट जानकारी की परस्पर क्रिया प्रदान करता है। (आईटीयू टी जी.806)। विषय: दूरसंचार, EN परत की बुनियादी अवधारणाएँ... ... तकनीकी अनुवादक की मार्गदर्शिका