สูตรทั่วไปของไซน์ในตรีโกณมิติ ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ - ทุกสิ่งที่คุณจำเป็นต้องรู้ที่ OGE และ USE
อัตราส่วนระหว่างฟังก์ชันตรีโกณมิติหลัก - ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ - ถูกกำหนด สูตรตรีโกณมิติ. และเนื่องจากมีความสัมพันธ์กันค่อนข้างมากระหว่างฟังก์ชันตรีโกณมิติ นี่จึงอธิบายความอุดมสมบูรณ์ของสูตรตรีโกณมิติด้วย บางสูตรเชื่อมโยงฟังก์ชันตรีโกณมิติของมุมเดียวกัน อื่นๆ - ฟังก์ชันของหลายมุม อื่นๆ - อนุญาตให้คุณลดดีกรีที่สี่ - เพื่อแสดงฟังก์ชันทั้งหมดผ่านแทนเจนต์ของครึ่งมุม ฯลฯ
ในบทความนี้ เราจะแสดงรายการสูตรตรีโกณมิติพื้นฐานทั้งหมดตามลำดับ ซึ่งเพียงพอสำหรับการแก้ปัญหาตรีโกณมิติส่วนใหญ่ เพื่อความสะดวกในการท่องจำและใช้งาน เราจะจัดกลุ่มตามจุดประสงค์ และป้อนลงในตาราง
การนำทางหน้า
เอกลักษณ์ตรีโกณมิติพื้นฐาน
เอกลักษณ์ตรีโกณมิติพื้นฐานกำหนดความสัมพันธ์ระหว่างไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมหนึ่ง พวกเขาติดตามจากนิยามของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ เช่นเดียวกับแนวคิดของวงกลมหน่วย สิ่งเหล่านี้ช่วยให้คุณแสดงฟังก์ชันตรีโกณมิติหนึ่งผ่านฟังก์ชันอื่น
สำหรับคำอธิบายโดยละเอียดของสูตรตรีโกณมิติเหล่านี้ ตัวอย่างที่มาและตัวอย่างการใช้งาน โปรดดูบทความ
สูตรหล่อ


สูตรหล่อตามมาจากคุณสมบัติของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ กล่าวคือ สะท้อนคุณสมบัติของคาบของฟังก์ชันตรีโกณมิติ สมบัติของสมมาตร และสมบัติของการเลื่อนตามมุมที่กำหนด สูตรตรีโกณมิติเหล่านี้ช่วยให้คุณเปลี่ยนจากการทำงานกับมุมใดก็ได้เป็นการทำงานกับมุมตั้งแต่ศูนย์ถึง 90 องศา
ศึกษาเหตุผลของสูตรเหล่านี้ กฎการช่วยจำสำหรับการท่องจำ และตัวอย่างการใช้งานสูตรเหล่านี้ได้ในบทความ
สูตรเสริม

สูตรบวกตรีโกณมิติแสดงว่าฟังก์ชันตรีโกณมิติของผลรวมหรือผลต่างของมุมทั้งสองแสดงออกมาอย่างไรในแง่ของฟังก์ชันตรีโกณมิติของมุมเหล่านี้ สูตรเหล่านี้เป็นพื้นฐานสำหรับการได้มาของสูตรตรีโกณมิติต่อไปนี้
สูตรดับเบิ้ล ทริปเปิ้ล ฯลฯ มุม


สูตรดับเบิ้ล ทริปเปิ้ล ฯลฯ มุม (เรียกอีกอย่างว่าสูตรหลายมุม) แสดงว่าฟังก์ชันตรีโกณมิติของสองเท่า สามเท่า ฯลฯ มุม () แสดงในรูปของฟังก์ชันตรีโกณมิติของมุมเดียว ที่มาของพวกเขาขึ้นอยู่กับสูตรการบวก
ข้อมูลรายละเอียดเพิ่มเติมถูกรวบรวมไว้ในบทความสูตรสำหรับสองเท่า สามเท่า ฯลฯ มุม .
สูตรครึ่งมุม

สูตรครึ่งมุมแสดงว่าฟังก์ชันตรีโกณมิติของครึ่งมุมแสดงในรูปของโคไซน์ของมุมจำนวนเต็มอย่างไร สูตรตรีโกณมิติเหล่านี้ตามมาจากสูตรมุมคู่
บทสรุปและตัวอย่างการสมัครสามารถพบได้ในบทความ
สูตรลด


สูตรตรีโกณมิติลดองศาได้รับการออกแบบมาเพื่ออำนวยความสะดวกในการเปลี่ยนจากพลังธรรมชาติของฟังก์ชันตรีโกณมิติไปเป็นไซน์และโคไซน์ในระดับแรก แต่มีหลายมุม กล่าวอีกนัยหนึ่ง พวกเขายอมลดกำลังของฟังก์ชันตรีโกณมิติเป็นอันดับแรก
สูตรสำหรับผลรวมและผลต่างของฟังก์ชันตรีโกณมิติ

จุดหมายหลัก สูตรผลรวมและผลต่างของฟังก์ชันตรีโกณมิติประกอบด้วยการเปลี่ยนไปใช้ผลคูณของฟังก์ชัน ซึ่งมีประโยชน์มากเมื่อลดความซับซ้อนของนิพจน์ตรีโกณมิติ สูตรเหล่านี้ยังใช้กันอย่างแพร่หลายในการแก้สมการตรีโกณมิติ เนื่องจากช่วยให้แยกตัวประกอบผลรวมและผลต่างของไซน์และโคไซน์
สูตรสำหรับผลคูณของไซน์ โคไซน์ และไซน์โดยโคไซน์

การเปลี่ยนจากผลคูณของฟังก์ชันตรีโกณมิติไปเป็นผลรวมหรือผลต่างจะดำเนินการโดยใช้สูตรสำหรับผลคูณของไซน์ โคไซน์ และไซน์โดยโคไซน์
ลิขสิทธิ์โดย นักเรียนฉลาด
สงวนลิขสิทธิ์.
ได้รับการคุ้มครองตามกฎหมายลิขสิทธิ์ ห้ามทำซ้ำส่วนหนึ่งของ www.site รวมถึงวัสดุภายในและการออกแบบภายนอกในรูปแบบใด ๆ หรือใช้โดยไม่ได้รับอนุญาตเป็นลายลักษณ์อักษรล่วงหน้าจากผู้ถือลิขสิทธิ์
เราเริ่มศึกษาตรีโกณมิติด้วยสามเหลี่ยมมุมฉาก ลองนิยามว่าไซน์และโคไซน์คืออะไร รวมทั้งแทนเจนต์และโคแทนเจนต์ของมุมแหลม เหล่านี้เป็นพื้นฐานของตรีโกณมิติ
จำได้ว่า มุมฉากเป็นมุมเท่ากับ 90 องศา กล่าวอีกนัยหนึ่งคือครึ่งหนึ่งของมุมที่กางออก
มุมแหลม- น้อยกว่า 90 องศา
มุมป้าน- มากกว่า 90 องศา ในความสัมพันธ์กับมุมดังกล่าว "ทื่อ" ไม่ใช่การดูถูก แต่เป็นศัพท์ทางคณิตศาสตร์ :-)
ลองวาดรูปสามเหลี่ยมมุมฉากกัน มุมฉากมักจะแสดง สังเกตว่าด้านตรงข้ามมุมเขียนด้วยอักษรตัวเดียวกัน ตัวพิมพ์เล็กเท่านั้น ดังนั้นด้านที่อยู่ตรงข้ามมุม A จึงถูกแสดง
มุมเขียนแทนด้วยตัวอักษรกรีกที่สอดคล้องกัน

ด้านตรงข้ามมุมฉากสามเหลี่ยมมุมฉากคือด้านตรงข้ามมุมฉาก
ขา- ด้านตรงข้ามมุมแหลมคม
ขาตรงข้ามมุมเรียกว่า ตรงข้าม(เทียบกับมุม). ขาอีกข้างหนึ่งนอนตะแคงข้างหนึ่งเรียกว่า ที่อยู่ติดกัน.
ไซนัสมุมแหลมในรูปสามเหลี่ยมมุมฉากคืออัตราส่วนของขาตรงข้ามกับด้านตรงข้ามมุมฉาก:
โคไซน์มุมแหลมในรูปสามเหลี่ยมมุมฉาก - อัตราส่วนของขาที่อยู่ติดกันต่อด้านตรงข้ามมุมฉาก:
แทนเจนต์มุมแหลมในรูปสามเหลี่ยมมุมฉาก - อัตราส่วนของขาตรงข้ามกับที่อยู่ติดกัน:
คำจำกัดความอื่น (เทียบเท่า): แทนเจนต์ของมุมแหลมคืออัตราส่วนของไซน์ของมุมหนึ่งต่อโคไซน์ของมัน:
โคแทนเจนต์มุมแหลมในรูปสามเหลี่ยมมุมฉาก - อัตราส่วนของขาที่อยู่ติดกันกับด้านตรงข้าม (หรืออัตราส่วนของโคไซน์ต่อไซน์เท่ากัน):
ให้ความสนใจกับอัตราส่วนพื้นฐานสำหรับไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ ซึ่งแสดงไว้ด้านล่าง จะเป็นประโยชน์ต่อเราในการแก้ปัญหา

มาพิสูจน์กันสักหน่อย
เอาล่ะเราได้ให้คำจำกัดความและสูตรที่เป็นลายลักษณ์อักษรแล้ว แต่ทำไมเราถึงต้องการไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์?
เรารู้ว่า ผลรวมของมุมของสามเหลี่ยมใดๆ คือ.
เรารู้ความสัมพันธ์ระหว่าง ปาร์ตี้สามเหลี่ยมมุมฉาก. นี่คือทฤษฎีบทพีทาโกรัส:
ปรากฎว่ารู้สองมุมในรูปสามเหลี่ยม คุณสามารถหามุมที่สามได้ เมื่อรู้สองด้านในสามเหลี่ยมมุมฉาก คุณสามารถหาด้านที่สามได้ ดังนั้น สำหรับมุม - อัตราส่วน สำหรับด้าน - ของมันเอง แต่จะทำอย่างไรถ้ารู้มุมหนึ่งในรูปสามเหลี่ยมมุมฉาก (ยกเว้นมุมขวา) และด้านใดด้านหนึ่ง แต่คุณต้องหาด้านอื่น

นี่คือสิ่งที่ผู้คนเผชิญในอดีต ทำแผนที่ของพื้นที่และท้องฟ้าเต็มไปด้วยดวงดาว ท้ายที่สุดแล้ว ไม่สามารถวัดทุกด้านของสามเหลี่ยมได้โดยตรงเสมอไป
ไซน์ โคไซน์ และแทนเจนต์ - เรียกอีกอย่างว่า ฟังก์ชันตรีโกณมิติของมุม- ให้อัตราส่วนระหว่าง ปาร์ตี้และ มุมสามเหลี่ยม. เมื่อรู้มุม คุณจะพบฟังก์ชันตรีโกณมิติทั้งหมดได้โดยใช้ตารางพิเศษ และเมื่อรู้ไซน์ โคไซน์ และแทนเจนต์ของมุมของสามเหลี่ยมและด้านใดด้านหนึ่ง คุณสามารถหาส่วนที่เหลือได้
เราจะวาดตารางค่าไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์สำหรับมุม "ดี" จาก ถึง
สังเกตเครื่องหมายขีดสีแดงสองอันในตาราง สำหรับค่าที่สอดคล้องกันของมุม ไม่มีแทนเจนต์และโคแทนเจนต์
มาวิเคราะห์ปัญหาตรีโกณมิติจากงาน Bank of FIPI กัน
1. ในรูปสามเหลี่ยมมุมฉากคือ , . หา .
ปัญหาได้รับการแก้ไขในสี่วินาที
เพราะว่า , .
2. ในรูปสามเหลี่ยมมุมฉากคือ , , . หา .

มาหาทฤษฎีบทพีทาโกรัสกัน
แก้ไขปัญหา.
บ่อยครั้งในปัญหามีรูปสามเหลี่ยมที่มีมุม และ หรือ กับมุม และ . จดจำอัตราส่วนพื้นฐานสำหรับพวกเขาด้วยใจ!

สำหรับรูปสามเหลี่ยมที่มีมุมและขาตรงข้ามมุมที่เท่ากับ ครึ่งหนึ่งของด้านตรงข้ามมุมฉาก.
สามเหลี่ยมที่มีมุมและเป็นหน้าจั่ว ด้านตรงข้ามมุมฉากมีขนาดใหญ่กว่าขาหลายเท่า
เราพิจารณาปัญหาในการแก้สามเหลี่ยมมุมฉาก นั่นคือ การหาด้านหรือมุมที่ไม่รู้จัก แต่นั่นไม่ใช่ทั้งหมด! ในรูปแบบข้อสอบคณิตศาสตร์ มีงานหลายอย่างที่ไซน์ โคไซน์ แทนเจนต์หรือโคแทนเจนต์ของมุมด้านนอกของรูปสามเหลี่ยมปรากฏขึ้น เพิ่มเติมเกี่ยวกับเรื่องนี้ในบทความถัดไป
ฉันจะไม่โน้มน้าวคุณไม่ให้เขียนแผ่นโกง เขียน! รวมสูตรตรีโกณมิติด้วย ต่อมาฉันวางแผนที่จะอธิบายว่าทำไมต้องมีแผ่นโกงและแผ่นโกงมีประโยชน์อย่างไร และที่นี่ - ข้อมูลเกี่ยวกับวิธีที่จะไม่เรียนรู้ แต่ต้องจำสูตรตรีโกณมิติบางสูตร ดังนั้น - ตรีโกณมิติที่ไม่มีแผ่นโกง!เราใช้การเชื่อมโยงสำหรับการท่องจำ
1. สูตรเพิ่มเติม:
โคไซน์มักจะ "เป็นคู่": โคไซน์-โคไซน์, ไซน์-ไซน์
และอีกสิ่งหนึ่ง: โคไซน์นั้น "ไม่เพียงพอ" พวกเขา "ทุกอย่างผิดปกติ" ดังนั้นพวกเขาจึงเปลี่ยนเครื่องหมาย: "-" เป็น "+" และในทางกลับกัน
ไซนัส - "ผสม": ไซน์-โคไซน์, โคไซน์-ไซน์
2. สูตรผลรวมและผลต่าง:
โคไซน์มักจะ "ไปเป็นคู่" เมื่อเพิ่มโคไซน์สองอัน - "ขนมปัง" เราได้โคไซน์หนึ่งคู่ - "koloboks" และการลบออก เราจะไม่ได้รับ koloboks แน่นอน เราได้ไซน์สองสามอัน ยังคงมีเครื่องหมายลบอยู่ข้างหน้า

ไซนัส - "ผสม" :

3. สูตรแปลงผลิตภัณฑ์เป็นผลรวมและส่วนต่าง
เราจะได้โคไซน์คู่หนึ่งเมื่อไหร่? เมื่อบวกโคไซน์ นั่นเป็นเหตุผลที่
เราจะได้คู่ของไซน์เมื่อไหร่? เมื่อลบโคไซน์ จากที่นี่:
"การผสม" ได้มาจากการบวกและการลบไซน์ อันไหนสนุกกว่ากัน: บวกหรือลบ? ถูกต้องพับ และสำหรับสูตรนี้ ให้เพิ่ม:
ในสูตรที่หนึ่งและสามในวงเล็บ - จำนวนเงิน จากการจัดเรียงตำแหน่งของเงื่อนไขใหม่ ผลรวมจะไม่เปลี่ยนแปลง ลำดับมีความสำคัญสำหรับสูตรที่สองเท่านั้น แต่เพื่อไม่ให้สับสนเพื่อให้จำง่ายทั้งสามสูตรในวงเล็บแรกเราจึงนำความแตกต่าง
และประการที่สอง ผลรวม
ผ้าปูเตียงในกระเป๋าช่วยให้อุ่นใจ: ถ้าคุณลืมสูตร คุณก็จดไว้ได้ และพวกเขาให้ความมั่นใจ: หากคุณไม่ได้ใช้สูตรโกงคุณสามารถจดจำสูตรได้ง่าย
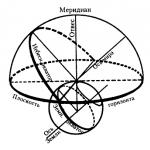
ตรีโกณมิติเป็นวิทยาศาสตร์ที่มีต้นกำเนิดมาจากตะวันออกโบราณ อัตราส่วนตรีโกณมิติแรกได้รับการพัฒนาโดยนักดาราศาสตร์เพื่อสร้างปฏิทินที่แม่นยำและปรับทิศทางของดวงดาว การคำนวณเหล่านี้เกี่ยวข้องกับตรีโกณมิติทรงกลม ในขณะที่ในหลักสูตรของโรงเรียน พวกเขาจะศึกษาอัตราส่วนของด้านและมุมของรูปสามเหลี่ยมแบนราบ
ตรีโกณมิติเป็นสาขาหนึ่งของคณิตศาสตร์ที่เกี่ยวข้องกับคุณสมบัติของฟังก์ชันตรีโกณมิติและความสัมพันธ์ระหว่างด้านและมุมของสามเหลี่ยม
ในช่วงรุ่งเรืองของวัฒนธรรมและวิทยาศาสตร์ในสหัสวรรษที่ 1 ความรู้แพร่กระจายจากตะวันออกโบราณไปยังกรีซ แต่การค้นพบตรีโกณมิติที่สำคัญคือข้อดีของชาวอาหรับหัวหน้าศาสนาอิสลาม โดยเฉพาะอย่างยิ่งนักวิทยาศาสตร์ชาวเติร์กเมนิสถาน al-Marazvi ได้แนะนำฟังก์ชันเช่นแทนเจนต์และโคแทนเจนต์ซึ่งรวบรวมตารางค่าแรกสำหรับไซน์แทนเจนต์และโคแทนเจนต์ นักวิทยาศาสตร์ชาวอินเดียแนะนำแนวคิดของไซน์และโคไซน์ ความสนใจอย่างมากเกี่ยวกับตรีโกณมิติในงานของตัวเลขที่ยิ่งใหญ่ในสมัยโบราณเช่น Euclid, Archimedes และ Eratosthenes
ปริมาณพื้นฐานของตรีโกณมิติ
ฟังก์ชันตรีโกณมิติพื้นฐานของอาร์กิวเมนต์เชิงตัวเลข ได้แก่ ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ แต่ละคนมีกราฟของตัวเอง: ไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์
สูตรการคำนวณค่าของปริมาณเหล่านี้ขึ้นอยู่กับทฤษฎีบทพีทาโกรัส เป็นที่รู้จักกันดีในหมู่เด็กนักเรียนในสูตร: "กางเกงพีทาโกรัสเท่ากันในทุกทิศทาง" เนื่องจากมีการให้การพิสูจน์ในตัวอย่างสามเหลี่ยมมุมฉากหน้าจั่ว
ไซน์ โคไซน์ และการพึ่งพาอื่นๆ สร้างความสัมพันธ์ระหว่างมุมแหลมและด้านของสามเหลี่ยมมุมฉากใดๆ เราให้สูตรสำหรับคำนวณปริมาณเหล่านี้สำหรับมุม A และติดตามความสัมพันธ์ของฟังก์ชันตรีโกณมิติ:

อย่างที่คุณเห็น tg และ ctg เป็นฟังก์ชันผกผัน หากเราแทนขา a เป็นผลคูณของบาป A และด้านตรงข้ามมุมฉาก c และขา b เป็น cos A * c เราก็จะได้สูตรต่อไปนี้สำหรับแทนเจนต์และโคแทนเจนต์:

วงกลมตรีโกณมิติ
ในรูปกราฟ อัตราส่วนของปริมาณดังกล่าวสามารถแสดงได้ดังนี้:

ในกรณีนี้ วงกลมแทนค่าที่เป็นไปได้ทั้งหมดของมุม α - ตั้งแต่ 0 ° ถึง 360 ° ดังที่เห็นได้จากรูปภาพ แต่ละฟังก์ชันใช้ค่าลบหรือค่าบวกขึ้นอยู่กับมุม ตัวอย่างเช่น sin α จะมีเครื่องหมาย "+" หาก α อยู่ในไตรมาส I และ II ของวงกลม นั่นคืออยู่ในช่วง 0 ° ถึง 180 ° ด้วย α จาก 180° ถึง 360° (III และ IV ควอเตอร์) sin α สามารถเป็นค่าลบได้เท่านั้น
มาลองสร้างตารางตรีโกณมิติสำหรับมุมเฉพาะและหาความหมายของปริมาณกัน

ค่าของ α เท่ากับ 30°, 45°, 60°, 90°, 180° เป็นต้น เรียกว่ากรณีพิเศษ ค่าของฟังก์ชันตรีโกณมิติสำหรับพวกเขาจะคำนวณและนำเสนอในรูปแบบของตารางพิเศษ

มุมเหล่านี้ไม่ได้ถูกเลือกโดยบังเอิญ การกำหนด π ในตารางใช้สำหรับเรเดียน Rad คือมุมที่ความยาวของส่วนโค้งวงกลมสอดคล้องกับรัศมีของมัน ค่านี้ถูกนำมาใช้เพื่อสร้างความสัมพันธ์แบบสากล เมื่อคำนวณเป็นเรเดียน ความยาวที่แท้จริงของรัศมีเป็นซม. ไม่สำคัญ

มุมในตารางสำหรับฟังก์ชันตรีโกณมิติสอดคล้องกับค่าเรเดียน:

ดังนั้นจึงไม่ยากที่จะเดาว่า 2π เป็นวงกลมเต็มหรือ 360°
สมบัติของฟังก์ชันตรีโกณมิติ: ไซน์และโคไซน์
ในการพิจารณาและเปรียบเทียบคุณสมบัติพื้นฐานของไซน์และโคไซน์ แทนเจนต์ และโคแทนเจนต์ จำเป็นต้องวาดฟังก์ชันของพวกมัน ซึ่งสามารถทำได้ในรูปของเส้นโค้งที่อยู่ในระบบพิกัดสองมิติ
พิจารณาตารางคุณสมบัติเปรียบเทียบสำหรับคลื่นไซน์และคลื่นโคไซน์:

| ไซนัส | คลื่นโคไซน์ |
|---|---|
| y = บาป x | y = cos x |
| โอดีซี [-1; หนึ่ง] | โอดีซี [-1; หนึ่ง] |
| บาป x = 0 สำหรับ x = πk โดยที่ k ϵ Z | cos x = 0, สำหรับ x = π/2 + πk โดยที่ k ϵ Z |
| บาป x = 1 สำหรับ x = π/2 + 2πk โดยที่ k ϵ Z | cos x = 1 สำหรับ x = 2πk โดยที่ k ϵ Z |
| บาป x = - 1 ที่ x = 3π/2 + 2πk โดยที่ k ϵ Z | cos x = - 1 สำหรับ x = π + 2πk โดยที่ k ϵ Z |
| บาป (-x) = - บาป x คือฟังก์ชันคี่ | cos (-x) = cos x นั่นคือฟังก์ชันเป็นคู่ |
| ฟังก์ชันเป็นแบบคาบ คาบที่เล็กที่สุดคือ 2π | |
| บาป x › 0, โดยที่ x อยู่ในควอเตอร์ I และ II หรือจาก 0° ถึง 180° (2πk, π + 2πk) | cos x › 0 โดยที่ x อยู่ในควอเตอร์ I และ IV หรือจาก 270 ถึง 90° (- π/2 + 2πk, π/2 + 2πk) |
| บาป x ‹ 0 โดย x อยู่ในควอเตอร์ III และ IV หรือจาก 180° ถึง 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0 โดย x อยู่ในไตรมาส II และ III หรือจาก 90° ถึง 270° (π/2 + 2πk, 3π/2 + 2πk) |
| เพิ่มขึ้นตามช่วงเวลา [- π/2 + 2πk, π/2 +2πk] | เพิ่มขึ้นในช่วงเวลา [-π + 2πk, 2πk] |
| ลดลงตามช่วงเวลา [ π/2 + 2πk, 3π/2 + 2πk] | ลดลงเป็นระยะ |
| อนุพันธ์ (sin x)' = cos x | อนุพันธ์ (cos x)’ = - บาป x |
การพิจารณาว่าฟังก์ชันมีค่าเท่ากันหรือไม่นั้นง่ายมาก ก็เพียงพอแล้วที่จะจินตนาการถึงวงกลมตรีโกณมิติที่มีสัญญาณของปริมาณตรีโกณมิติและ "พับ" กราฟที่สัมพันธ์กับแกน OX ในทางจิตใจ ถ้าเครื่องหมายเหมือนกัน ฟังก์ชันจะเป็นคู่ ไม่เช่นนั้น จะเป็นเลขคี่

การแนะนำเรเดียนและการแจงนับคุณสมบัติหลักของคลื่นไซนัสและโคไซน์ช่วยให้เราสามารถนำมาซึ่งความสม่ำเสมอดังต่อไปนี้:

การตรวจสอบความถูกต้องของสูตรทำได้ง่ายมาก ตัวอย่างเช่น สำหรับ x = π/2 ไซน์จะเท่ากับ 1 เช่นเดียวกับโคไซน์ของ x = 0 การตรวจสอบสามารถทำได้โดยดูที่ตารางหรือโดยการติดตามเส้นโค้งฟังก์ชันสำหรับค่าที่กำหนด
คุณสมบัติของแทนเจนต์และโคแทนเจนตอยด์
กราฟของฟังก์ชันแทนเจนต์และโคแทนเจนต์แตกต่างกันอย่างมีนัยสำคัญจากคลื่นไซนัสและโคไซน์ ค่า tg และ ctg จะกลับกัน


- Y = tgx.
- แทนเจนต์มีแนวโน้มที่จะเป็นค่าของ y ที่ x = π/2 + πk แต่ไม่เคยไปถึงค่าเหล่านั้น
- คาบบวกที่เล็กที่สุดของแทนเจนต์ทอยด์คือ π
- Tg (- x) \u003d - tg x นั่นคือฟังก์ชันเป็นเลขคี่
- Tg x = 0 สำหรับ x = πk
- ฟังก์ชั่นที่เพิ่มขึ้น
- Tg x › 0 สำหรับ x ϵ (πk, π/2 + πk)
- Tg x ‹ 0 สำหรับ x ϵ (— π/2 + πk, πk)
- อนุพันธ์ (tg x)' = 1/cos 2 x
พิจารณาการแสดงกราฟิกของ cotangentoid ด้านล่างในข้อความ

คุณสมบัติหลักของ cotangentoid:
- Y = ctgx.
- ฟังก์ชันไซน์และโคไซน์ต่างจากฟังก์ชันไซน์และโคไซน์ในแทนเจนต์ทอยด์ Y สามารถใช้ค่าของเซตของจำนวนจริงทั้งหมดได้
- cotangentoid มีแนวโน้มที่จะมีค่าของ y ที่ x = πk แต่ไม่เคยไปถึงค่าเหล่านั้น
- คาบบวกที่เล็กที่สุดของโคแทนเจนตอยด์คือ π
- Ctg (- x) \u003d - ctg x นั่นคือฟังก์ชันเป็นเลขคี่
- Ctg x = 0 สำหรับ x = π/2 + πk
- ฟังก์ชันกำลังลดลง
- Ctg x › 0, สำหรับ x ϵ (πk, π/2 + πk)
- Ctg x ‹ 0 สำหรับ x ϵ (π/2 + πk, πk)
- อนุพันธ์ (ctg x)' = - 1/sin 2 x Fix