รูปแบบทางเรขาคณิตสำหรับกำหนดความน่าจะเป็น คำจำกัดความทางเรขาคณิตของความน่าจะเป็นของเหตุการณ์
ดังที่แสดงไว้ในส่วนคำจำกัดความคลาสสิกของความน่าจะเป็น ในการทดลองสุ่มที่มีผลลัพธ์เบื้องต้นเท่าๆ กันจำนวนจำกัดสมัครแล้ว ความหมายคลาสสิกของความน่าจะเป็น.
เพื่อแนะนำความน่าจะเป็นของเหตุการณ์ในการทดลองสุ่ม ผลลัพธ์ที่เป็นไปได้ (ผลลัพธ์เบื้องต้น) ก็เช่นกัน เป็นไปได้อย่างเท่าเทียมกันและ เติมเต็มช่องว่างเส้นตรง, รูปบนเครื่องบินหรือ ภาคในอวกาศนำไปใช้ ความหมายทางเรขาคณิตของความน่าจะเป็น. ในการทดลองดังกล่าว จำนวนผลลัพธ์เบื้องต้น ยังไม่จบดังนั้นจึงไม่สามารถใช้คำจำกัดความคลาสสิกของความน่าจะเป็นได้
ให้เราแสดงการแนะนำคำนิยามทางเรขาคณิตของความน่าจะเป็นพร้อมตัวอย่าง
ตัวอย่างที่ 1 . จะมีการสุ่มจุดหนึ่งจุดบนส่วนของเส้นจำนวน ค้นหาความน่าจะเป็นที่จุดนั้นตกบนเซ็กเมนต์ (รูปที่ 1)


ตอบ:
ตัวอย่างที่ 2 . เส้นทแยงมุม KM และ LN ของสี่เหลี่ยมจัตุรัส KLMN ตัดกับวงกลมที่จารึกไว้ในสี่เหลี่ยมจัตุรัสที่จุด E และ F จุด O เป็นจุดศูนย์กลางของวงกลม (รูปที่ 2)

จุดจะถูกสุ่มใส่ลงในสี่เหลี่ยม KLMN หาความน่าจะเป็นที่จุดนั้นจะตกลงไปในภาค EOF ที่มีเครื่องหมายสีชมพูในรูปที่ 2

ตอบ:
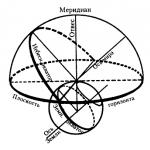
ตัวอย่างที่ 3 . สุ่มจุดหนึ่งลงในกรวยที่มีจุดยอด S และจุดศูนย์กลางฐาน O ค้นหาความน่าจะเป็นที่จุดจะตกลงไปในกรวยที่ถูกตัดทอน ซึ่งได้จากการตัดกรวยโดยให้ระนาบผ่านจุดกึ่งกลาง O "ของความสูงของกรวยและขนานกับฐานของกรวย (รูปที่ 3)


วิธีการแก้ . เซตของผลลัพธ์เบื้องต้น Ω ของการทดลองสุ่มในการโยนจุดหนึ่งๆ คือเซตของจุดทั้งหมดของกรวยที่มีจุดยอด S และจุดศูนย์กลางฐาน O
การชนจุดหนึ่งในกรวยที่ถูกตัดทอนเป็นหนึ่งในเหตุการณ์สุ่ม ซึ่งเราจะแสดงด้วยตัวอักษร A
ที่ ความหมายทางเรขาคณิต ความน่าจะเป็นของเหตุการณ์ A คำนวณโดยสูตร
ให้ R เป็นรัศมีของฐานของกรวยที่มีจุดยอด S และศูนย์กลางฐาน O และให้ H เป็นความสูงของกรวยนี้ จากนั้นรัศมีของฐานและความสูงของกรวยที่มีจุดยอด S และจุดศูนย์กลางของฐาน O" จะเท่ากับ
ตามลำดับ
ปริมาตรของกรวยที่มีจุดยอด S และจุดศูนย์กลางฐาน O คือ
คำจำกัดความดั้งเดิมของความน่าจะเป็นมีข้อจำกัดในการใช้งาน สันนิษฐานว่าชุดของเหตุการณ์เบื้องต้น Ω มีขอบเขตหรือนับได้ นั่นคือ Ω = ( ω 1 , ω 2 , … , ω n , …) และทั้งหมด ω ผม – เหตุการณ์ระดับประถมศึกษาที่เป็นไปได้เท่าๆ กัน อย่างไรก็ตาม ในทางปฏิบัติ มีการทดสอบที่ชุดของผลลัพธ์เบื้องต้นนั้นไม่มีที่สิ้นสุด ตัวอย่างเช่น เมื่อผลิตชิ้นส่วนบางอย่างบนเครื่องจักร จำเป็นต้องรักษาขนาดที่แน่นอน ความแม่นยำในการผลิตชิ้นส่วนขึ้นอยู่กับทักษะของผู้ปฏิบัติงาน คุณภาพของเครื่องมือตัด ความสมบูรณ์ของเครื่องจักร ฯลฯ หากเข้าใจว่าการทดสอบเป็นการผลิตชิ้นส่วน ผลของการทดสอบดังกล่าวจะทำให้ได้ผลลัพธ์จำนวนอนันต์ ในกรณีนี้ เพื่อให้ได้ชิ้นส่วนที่มีขนาดที่ต้องการ
เพื่อเอาชนะจุดอ่อนของนิยามความน่าจะเป็นแบบคลาสสิก บางครั้งจึงใช้แนวคิดบางประการเกี่ยวกับเรขาคณิต (หากแน่นอน สถานการณ์ของการทดสอบเอื้ออำนวย) ในกรณีดังกล่าวทั้งหมด มีความเป็นไปได้ที่จะทำการทดสอบ (อย่างน้อยในทางทฤษฎี) จำนวนเท่าใดก็ได้ และแนวคิด โอกาสที่เท่าเทียมกันยังมีบทบาทสำคัญ
ให้ทดสอบด้วยช่องว่างของเหตุการณ์ ผลลัพธ์เบื้องต้นแสดงเป็นจุดเติมบางพื้นที่ Ω (ในช่องว่างสามมิติ R 3). ให้เหตุการณ์ แต่ประกอบด้วยการสุ่มเลือกจุดโยนในโดเมนย่อย ดีโดเมน Ω เหตุการณ์ แต่โปรดปรานเหตุการณ์เบื้องต้นที่ประเด็นตกอยู่ในโดเมนย่อยบางส่วน ดี. แล้ว ภายใต้ความน่าจะเป็นพัฒนาการ แต่เราจะเข้าใจอัตราส่วนของปริมาตรของโดเมนย่อย ดี(เน้นพื้นที่ในรูป 1.11) กับปริมาตรของพื้นที่ Ω, R(แต่) = วี(ดี) / วี(Ω).
|
ข้าว.1. 11 |
ในที่นี้ โดยการเปรียบเทียบกับแนวคิดของผลลัพธ์ที่ดี พื้นที่ ดีจะเรียกว่าเป็นมงคลต่อรูปลักษณ์ของงาน แต่. ความน่าจะเป็นของเหตุการณ์ถูกกำหนดในทำนองเดียวกัน แต่,เมื่อเซต Ω คือพื้นที่หนึ่งบนระนาบหรือส่วนที่เป็นเส้นตรง ในกรณีเหล่านี้ ปริมาตรของพื้นที่จะถูกแทนที่ด้วยพื้นที่ของตัวเลขหรือความยาวของส่วนตามลำดับ
ดังนั้นเราจึงได้นิยามใหม่ว่า ความน่าจะเป็นทางเรขาคณิตสำหรับการทดสอบด้วยชุดเหตุการณ์เบื้องต้นนับไม่ถ้วนซึ่งกำหนดได้ดังนี้
ความน่าจะเป็นทางเรขาคณิตของเหตุการณ์ A คืออัตราส่วนของการวัดของโดเมนย่อยที่สนับสนุนการเกิดของเหตุการณ์นี้ต่อการวัดพื้นที่ทั้งหมด กล่าวคือ
p(A) =mesD / เมสΩ,
ที่ไหน เมส– การวัดพื้นที่ ดีและ Ω , ดี Ì Ω.
ความน่าจะเป็นทางเรขาคณิตของเหตุการณ์มีคุณสมบัติทั้งหมดที่มีอยู่ในคำจำกัดความคลาสสิกของความน่าจะเป็น ตัวอย่างเช่น คุณสมบัติที่ 4 จะเป็น: R(แต่+ ที่) = R(แต่) + R(ที่).
ความหมายคลาสสิกของความน่าจะเป็น
แนวคิดพื้นฐานของทฤษฎีความน่าจะเป็นคือแนวคิดของเหตุการณ์สุ่ม เหตุการณ์สุ่มมักจะถูกเรียกว่าเหตุการณ์ ĸฟุตบอลนี้ หรืออาจไม่เกิดขึ้นก็ได้ ตัวอย่างเช่น การกดปุ่มหรือพลาดวัตถุเมื่อยิงไปที่วัตถุนี้ด้วยอาวุธที่กำหนดเป็นเหตุการณ์แบบสุ่ม
เหตุการณ์มักจะเรียกว่าเชื่อถือได้หากจำเป็นต้องเกิดขึ้นเนื่องจากการทดสอบ เป็นเรื่องปกติที่จะเรียกเหตุการณ์ที่เป็นไปไม่ได้ ĸᴏᴛᴏᴩᴏᴇ ไม่สามารถเกิดขึ้นจากการทดสอบได้
มีการกล่าวถึงเหตุการณ์สุ่มว่าไม่สอดคล้องกันในการทดลองหนึ่งๆ หากไม่มีเหตุการณ์สองเหตุการณ์ปรากฏขึ้นพร้อมกัน
เหตุการณ์สุ่มจะรวมกันเป็นกลุ่มที่สมบูรณ์ หากมีเหตุการณ์ใดปรากฏขึ้นในการทดลองแต่ละครั้ง และไม่มีเหตุการณ์อื่นที่ไม่สอดคล้องกับเหตุการณ์ปรากฏขึ้น
พิจารณากลุ่มที่สมบูรณ์ของเหตุการณ์สุ่มที่เข้ากันไม่ได้ที่เท่าเทียมกัน เหตุการณ์ดังกล่าวจะเรียกว่าผลลัพธ์ กล่าวได้ว่าผลลัพธ์เป็นผลดีต่อการเกิดเหตุการณ์ A หากการเกิดของเหตุการณ์นี้ทำให้เกิดเหตุการณ์ A
ความหมายทางเรขาคณิตของความน่าจะเป็น
ให้คิดว่าการทดสอบแบบสุ่มเป็นการสุ่มจุดหนึ่งไปยังบริเวณเรขาคณิต G (บนเส้น เครื่องบิน หรือช่องว่าง) ผลลัพธ์เบื้องต้นคือ ϶คะแนนของ G ที่แยกจากกัน, เหตุการณ์ใดๆ ก็ตามที่เป็นสับเซตของพื้นที่นี้, ช่องว่างของผลลัพธ์เบื้องต้น G เราสามารถสรุปได้ว่าจุด G ทั้งหมดนั้น ''เท่ากับ'' และจากนั้นความน่าจะเป็นของจุดที่ตกลงไปในหนึ่งใน เซตย่อย ĸᴏᴛᴏᴩᴏᴇ เป็นสัดส่วนกับการวัด (ความยาว พื้นที่ ปริมาตร) และไม่ขึ้นอยู่กับตำแหน่งและรูปร่าง
ความน่าจะเป็นทางเรขาคณิตเหตุการณ์ A ถูกกำหนดโดยความสัมพันธ์ โดยที่ m(G), m(A) คือการวัดทางเรขาคณิต (ความยาว พื้นที่ หรือปริมาตร) ของพื้นที่ทั้งหมดของผลลัพธ์เบื้องต้นและเหตุการณ์ A
ตัวอย่าง.วงกลมรัศมี r () สุ่มโยนลงบนระนาบ คั่นด้วยแถบความกว้าง 2d ขนานกัน ระยะห่างระหว่างเส้นแกนซึ่งเป็น 2D หาความน่าจะเป็นที่วงกลมตัดกับแถบบางเส้น
วิธีการแก้.ผลลัพธ์เบื้องต้นของการทดสอบนี้ เราจะพิจารณาระยะทาง xจากจุดศูนย์กลางของวงกลมถึงเส้นกึ่งกลางของแถบที่ใกล้กับวงกลมมากที่สุด จากนั้นพื้นที่ทั้งหมดของผลลัพธ์เบื้องต้น - ส่วน ϶คะแนน จุดตัดของวงกลมกับแถบนั้นจะเกิดขึ้นหากจุดศูนย์กลางตกลงไปในแถบ ᴛ.ᴇ หรือจะอยู่ห่างจากขอบแถบในระยะน้อยกว่ารัศมี .
สำหรับความน่าจะเป็นที่ต้องการ เราได้รับ:
5. ความถี่สัมพัทธ์ของเหตุการณ์คืออัตราส่วนของจำนวนการทดลองที่เหตุการณ์เกิดขึ้นกับจำนวนการทดลองที่ดำเนินการจริงทั้งหมด Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, ความถี่สัมพัทธ์ A ถูกกำหนดโดย:
(2)โดยที่ m คือจำนวนครั้งของเหตุการณ์ n คือจำนวนการทดลองทั้งหมด. เมื่อเปรียบเทียบคำจำกัดความของความน่าจะเป็นและความถี่สัมพัทธ์ เราสรุปได้ว่า: คำจำกัดความของความน่าจะเป็นไม่จำเป็นต้องทำการทดสอบในความเป็นจริง คำจำกัดความของความถี่สัมพัทธ์ถือว่าการทดสอบได้ดำเนินการจริง กล่าวอีกนัยหนึ่ง ความน่าจะเป็นจะถูกคำนวณก่อนประสบการณ์ และความถี่สัมพัทธ์จะถูกคำนวณหลังจากประสบการณ์
ตัวอย่างที่ 2 จากพนักงานที่สุ่มเลือก 80 คน มี 3 คนที่มีความผิดปกติของหัวใจอย่างร้ายแรง ความถี่สัมพัทธ์ของผู้ที่เป็นโรคหัวใจ
ความถี่สัมพัทธ์หรือตัวเลขที่ใกล้เคียงกันถือเป็นความน่าจะเป็นแบบคงที่
คำจำกัดความ (คำจำกัดความทางสถิติของความน่าจะเป็น) จำนวนที่ความถี่สัมพัทธ์คงที่มักจะเรียกว่าความน่าจะเป็นทางสถิติของเหตุการณ์นี้
6. ผลรวม A+B สองเหตุการณ์ A และ B ตั้งชื่อเหตุการณ์ที่ประกอบด้วยเหตุการณ์ A หรือเหตุการณ์ B หรือทั้งสองเหตุการณ์ ตัวอย่างเช่น หากการยิงสองนัดจากปืนและ A - ยิงในนัดแรก, B - ยิงในนัดที่สอง จากนั้น A + B - ยิงในนัดแรก หรือในนัดที่สอง หรือในทั้งสองนัด
โดยเฉพาะอย่างยิ่ง ถ้าสองเหตุการณ์ A และ B ไม่เข้ากัน A + B จะเป็นเหตุการณ์ที่ประกอบด้วยลักษณะที่ปรากฏของหนึ่งในเหตุการณ์เหล่านี้ ไม่ว่าเหตุการณ์ใดจะเกิดขึ้น ผลรวมของหลายเหตุการณ์เรียกว่าเหตุการณ์, ĸᴏᴛᴏᴩᴏᴇ ประกอบด้วยการเกิดขึ้นของเหตุการณ์เหล่านี้อย่างน้อยหนึ่งเหตุการณ์ ตัวอย่างเช่น เหตุการณ์ A + B + C ประกอบด้วยเหตุการณ์ใดเหตุการณ์หนึ่งต่อไปนี้ A, B, C, A และ B, A และ C, B และ C, A และ B และ C ให้เหตุการณ์ A และ B เข้ากันไม่ได้และความน่าจะเป็นของเหตุการณ์เหล่านี้เป็นที่รู้จัก จะค้นหาความน่าจะเป็นที่เหตุการณ์ A หรือเหตุการณ์ B จะเกิดขึ้นได้อย่างไร คำตอบสำหรับคำถามนี้มาจากทฤษฎีบทการบวก ทฤษฎีบท. ความน่าจะเป็นที่จะเกิดขึ้นของหนึ่งในสองเหตุการณ์ที่เข้ากันไม่ได้ ไม่ว่าเหตุการณ์ใดจะเท่ากับผลรวมของความน่าจะเป็นของเหตุการณ์เหล่านี้:
P (A + B) = P (A) + P (B) หลักฐาน
ข้อพิสูจน์ ความน่าจะเป็นที่จะเกิดขึ้นของหนึ่งในหลายเหตุการณ์ที่เข้ากันไม่ได้ ไม่ว่าจะเป็นเหตุการณ์ใด เท่ากับผลรวมของความน่าจะเป็นของเหตุการณ์เหล่านี้:
P (A 1 + A 2 + ... + A n) \u003d P (A 1) + P (A 2) + ... + P (A n)
ความหมายทางเรขาคณิตของความน่าจะเป็น - แนวคิดและประเภท การจำแนกประเภทและคุณสมบัติของหมวดหมู่ "คำจำกัดความทางเรขาคณิตของความน่าจะเป็น" 2017, 2018
ในทางปฏิบัติ มักพบการทดลองดังกล่าว โดยจำนวนผลลัพธ์ที่เป็นไปได้นั้นไม่มีที่สิ้นสุด บางครั้งในกรณีเช่นนี้ คุณสามารถใช้วิธีการคำนวณความน่าจะเป็นได้ ซึ่งแนวคิดของความเท่าเทียมกันของเหตุการณ์บางอย่างยังคงมีบทบาทหลัก .... .
ในสี่เหลี่ยมจัตุรัสหนึ่งจุดจะถูกสุ่มเลือกความน่าจะเป็นที่จุดนี้จะอยู่ในพื้นที่ D. โดยที่ SD คือพื้นที่ของภูมิภาค D, S คือพื้นที่ทั้งหมด สี่เหลี่ยม. ภายใต้คลาสสิก ความน่าจะเป็นศูนย์บางอย่างมี ... .
เพื่อเอาชนะข้อเสียของคำจำกัดความคลาสสิกของความน่าจะเป็น ซึ่งใช้ไม่ได้กับการทดลองที่มีผลลัพธ์จำนวนไม่สิ้นสุด เราจึงแนะนำความน่าจะเป็นทางเรขาคณิต - ความน่าจะเป็นของจุดที่ตกลงไปในพื้นที่ ให้หุ่นแบน g (ส่วนหรือตัว)... .
คำจำกัดความคลาสสิกของความน่าจะเป็น การบรรยาย 1. ทฤษฎีความน่าจะเป็น ประวัติความเป็นมา คำจำกัดความคลาสสิกของความน่าจะเป็น A.A. Khalafyan BIBLIOGRAPHICAL ข้อมูลอ้างอิง 1. Kolemaev V.A. , Staroverov O.V. , Turundaevsky V.B. ทฤษฎี ... .[อ่านเพิ่มเติม] .
คำจำกัดความนี้ใช้เมื่อประสบการณ์มีชุดผลลัพธ์ที่เป็นไปได้เท่าๆ กันที่นับไม่ได้ ในกรณีนี้ พื้นที่ของเหตุการณ์ระดับประถมศึกษาสามารถแสดงเป็นภูมิภาค G แต่ละจุดของภูมิภาคนี้สอดคล้องกับเหตุการณ์ระดับประถมศึกษา ตี... .
คำจำกัดความทางเรขาคณิตของความน่าจะเป็นเป็นการขยายแนวคิดของความน่าจะเป็นแบบคลาสสิกไปยังกรณีของชุดเหตุการณ์เบื้องต้นที่นับไม่ได้ ในกรณีที่เป็นเซตที่นับไม่ได้ ความน่าจะเป็นไม่ได้ถูกกำหนดในเหตุการณ์เบื้องต้น แต่สำหรับเซตของพวกมัน.... .
คำจำกัดความคลาสสิกของความน่าจะเป็นของเหตุการณ์สุ่ม การตีความทฤษฎีชุดของการดำเนินการกับเหตุการณ์ ให้การทดลองบางอย่างดำเนินการด้วยผลลัพธ์แบบสุ่ม เยอะ &... .
สูตร P(A)=m/n จะสูญเสียความหมายไป หากจำนวนเคสที่เข้ากันไม่ได้ทั้งหมดที่เป็นไปได้มีไม่จำกัด (รูปแบบชุดอนันต์) อย่างไรก็ตาม บางครั้งก็เป็นไปได้ที่จะกำหนดคุณลักษณะเชิงปริมาณ S ในการวัดความยาว พื้นที่ ปริมาตร เวลา และอื่นๆ ให้กับทั้งชุดของกรณีที่เข้ากันไม่ได้ที่เท่าเทียมกันที่เป็นไปได้อย่างไม่มีที่สิ้นสุด และให้ส่วนหนึ่งของชุดนี้ที่สนับสนุน การเริ่มต้นของเหตุการณ์ A ที่อยู่ระหว่างการพิจารณา เพื่อให้คุณลักษณะ S b อยู่ในเกณฑ์เดียวกัน จากนั้นความน่าจะเป็นของเหตุการณ์ A จะถูกกำหนดโดยความสัมพันธ์:
ตัวอย่าง # 1 ตัวเลขสองตัว x และ y จะถูกสุ่มเลือกจากช่วงเวลา จงหาความน่าจะเป็นที่ตัวเลขเหล่านี้เป็นไปตามอสมการ x 2 ≤ 4y ≤ 4x
วิธีการแก้.การทดสอบประกอบด้วยการเลือกสุ่มคู่ของตัวเลข x และ y จากช่วง เราจะตีความสิ่งนี้ว่าเป็นตัวเลือกแบบสุ่มของจุด M(x;y) จากเซตของจุดทุกจุดของสี่เหลี่ยมจัตุรัสที่มีด้านเท่ากับสอง ให้เราพิจารณารูป Ф ซึ่งเป็นเซตของจุดทุกจุดของสี่เหลี่ยมจัตุรัสที่มีพิกัดตรงตามระบบของความไม่เท่าเทียมกัน x 2 ≤ 4y ≤ 4x เหตุการณ์ที่น่าสนใจจะเกิดขึ้นก็ต่อเมื่อจุดที่เลือก M(x;y) เป็นของรูปที่ Ф 
ตามสูตร (8) ความน่าจะเป็นที่ต้องการจะเท่ากับอัตราส่วนของพื้นที่ของรูปที่ Ф ต่อพื้นที่ของสี่เหลี่ยมจัตุรัส: 
ตัวอย่าง # 2 ทั้งสองตกลงที่จะพบกัน ณ ที่แห่งหนึ่ง แต่ละคนมาถึงสถานที่นัดหมายโดยอิสระจากกันในช่วงเวลาสุ่มและรอไม่เกินเวลา ความน่าจะเป็นที่จะพบกันภายใต้เงื่อนไขดังกล่าวเป็นเท่าใด 
วิธีการแก้.ให้เราแสดงด้วย x เวลาที่มาถึงคนแรก ณ สถานที่ที่ตกลงกันไว้ และเมื่อถึงเวลาของบุคคลที่สองที่นั่น มันเป็นไปตามเงื่อนไขที่ x และ y ทำงานอย่างอิสระตลอดช่วงเวลา การทดสอบประกอบด้วยการกำหนดเวลาที่มาถึงของบุคคลที่ระบุไว้ ณ สถานที่นัดพบ จากนั้นพื้นที่ของผลลัพธ์เบื้องต้นของการทดลองนี้จะถูกตีความว่าเป็นเซตของจุดทั้งหมด M(x;y) ของสี่เหลี่ยมจัตุรัส Ω=((x;y) : 0 ≤ x ≤ T, 0 ≤ y ≤ T) เหตุการณ์ A ที่เราสนใจ - "การประชุมเกิดขึ้น" จะเกิดขึ้นก็ต่อเมื่อจุดที่เลือก M(x; y) อยู่ในรูป Ф ซึ่งเป็นเซตของจุดทุกจุดของสี่เหลี่ยม พิกัดที่ตรงตาม ความไม่เท่าเทียมกัน |x – y| ≤ ต. ตามสูตร (8) ความน่าจะเป็นที่ต้องการ
คืออัตราส่วนของพื้นที่ของรูปที่ Ф ต่อพื้นที่ของสี่เหลี่ยมจัตุรัส Ω:
![]()
จากการวิเคราะห์ผลลัพธ์ที่ได้จากปัญหานี้ เราจะเห็นว่าความน่าจะเป็นของการประชุมเพิ่มขึ้นตามการเพิ่มขึ้น ให้ตัวอย่างเช่น T = 1 ชั่วโมง t = 20 นาที แล้ว
ตัวอย่าง #3 สุ่มเลือกจุดสองจุดในส่วน l
พี(0 

ตัวอย่าง #4 สุ่มจุดหนึ่งจุดในวงกลมรัศมี r เพื่อให้ตำแหน่งใดๆ ในวงกลมเป็นไปได้เท่ากัน จงหาความน่าจะเป็นที่จะอยู่ภายในสี่เหลี่ยมจัตุรัสที่มีด้าน a อยู่ในวงกลม
วิธีการแก้. ความน่าจะเป็นที่จุดจะอยู่ภายในสี่เหลี่ยมที่อยู่ในวงกลมที่มีด้าน เอเท่ากับอัตราส่วนของพื้นที่สี่เหลี่ยมจัตุรัสกับพื้นที่ของวงกลม
พื้นที่สี่เหลี่ยมจัตุรัส: Skv \u003d a 2
พื้นที่วงกลม: S = πr 2
จากนั้นความน่าจะเป็นจะเป็น: p \u003d Skv / S \u003d a 2 / πr 2
ตัวอย่างหมายเลข 5 ตัวเลขจริงสองจำนวนจะถูกสุ่มเลือกจากช่วงเวลา จงหาความน่าจะเป็นที่ผลรวมของพวกมันมากกว่า 4 และผลิตภัณฑ์ของพวกมันน้อยกว่า 4
วิธีการแก้.
มีทั้งหมด 5 ตัวเลข: 0,1,2,3,4 ความน่าจะเป็นที่จะเกิดขึ้น p=1/5 = 0.2
ก) ความน่าจะเป็นที่ผลรวมของพวกเขาจะมากกว่า 4
จำนวนรวมของผลลัพธ์ดังกล่าวคือ 8:
1+4, 2+3, 2+4, 3+4 และ 4+1, 3+2, 4+2, 4+3
P = 0.2*0.2*8 = 0.32
b) สินค้ามีค่าน้อยกว่า 4
จำนวนรวมของผลลัพธ์ดังกล่าวคือ 13:
0*1, 0*2, 0*3, 0*4, 1*1, 1*2.1*3 และ 1*0, 2*0, 3*0, 4*0, 2*1, 3* หนึ่ง
P = 0.2*0.2*13 = 0.52
งานสำหรับโซลูชันอิสระ
4.3. หลังจากเกิดพายุ สายไฟขาดเกิดขึ้นที่ส่วนระหว่างสายโทรศัพท์ที่ระยะทาง 40 ถึง 70 กิโลเมตร ความน่าจะเป็นที่จะเกิดการแตกหักระหว่างกิโลเมตรที่ 45 ถึง 50 ของเส้นคืออะไร? (ความน่าจะเป็นของลวดขาดในที่ใดถือว่าเท่ากัน)
คำตอบ: 1/6.
4.4. สุ่มจุดหนึ่งจุดในวงกลมรัศมี r จงหาความน่าจะเป็นที่จุดนี้อยู่ในสามเหลี่ยมปกติที่จารึกไว้ในวงกลมที่กำหนด
ตอบ:
4.5. ค้นหาความน่าจะเป็นที่ผลรวมของตัวเลขสุ่มสองตัวที่สุ่มเลือกจากช่วง [-1; 1] มากกว่าศูนย์และผลิตภัณฑ์ของมันคือลบ
คำตอบ: 0.25
4.6. ระหว่างการฝึกรบ ฝูงบินทิ้งระเบิดที่ n ได้รับภารกิจโจมตีคลังน้ำมัน "ศัตรู" บนอาณาเขตของคลังน้ำมันซึ่งมีรูปร่างเป็นสี่เหลี่ยมผืนผ้ามีด้านยาว 30 และ 50 ม. มีถังน้ำมันทรงกลมสี่ถังมีเส้นผ่านศูนย์กลางแต่ละอัน 10 ม. ค้นหาความน่าจะเป็นของการระเบิดโดยตรงของถังน้ำมันโดยระเบิดที่กระทบอาณาเขตของคลังน้ำมัน ถ้าระเบิดกระทบจุดใด ๆ ของฐานนี้ด้วยความน่าจะเป็นเท่ากัน
คำตอบ: π/15.
4.7. สุ่มเลือกจำนวนจริง x และ y สองจำนวนโดยสุ่มเพื่อให้ผลรวมของกำลังสองมีค่าน้อยกว่า 100 ความน่าจะเป็นที่ผลรวมของกำลังสองของตัวเลขเหล่านี้มากกว่า 64 เป็นเท่าใด
คำตอบ: 0;36.
4.8. เพื่อนสองคนตกลงที่จะพบกันระหว่างเวลา 13:00 น. ถึง 14:00 น. คนแรกที่มาถึงรอคนที่สองเป็นเวลา 20 นาทีแล้วจากไป กำหนดความน่าจะเป็นที่จะพบปะเพื่อนฝูงหากช่วงเวลาที่พวกเขามาถึงในช่วงเวลาที่กำหนดมีความน่าจะเป็นเท่ากัน
คำตอบ: 5/9
4.9. เรือกลไฟสองลำต้องมาที่ท่าเรือเดียวกัน เวลาที่มาถึงของเรือทั้งสองลำจะเท่ากันในวันที่กำหนด กำหนดความน่าจะเป็นที่เรือกลไฟคนใดคนหนึ่งจะต้องรอจนกว่าเรือจะออกหากเรือกลไฟลำแรกอยู่เป็นเวลาหนึ่งชั่วโมงและครั้งที่สองเป็นเวลาสองชั่วโมง
คำตอบ: ≈ 0;121.
4.10. สุ่มจำนวนบวกสองจำนวน x และ y โดยแต่ละจำนวนไม่เกินสอง จงหาความน่าจะเป็นที่ผลคูณ x y มีค่าเท่ากับหนึ่ง และผลคูณ y/x มีค่ามากสุดสอง
คำตอบ: ≈ 0;38.
4.11. ในพื้นที่ G ล้อมรอบด้วยทรงรี ![]() , จุดจะถูกกำหนดโดยการสุ่ม ความน่าจะเป็นที่พิกัด (x; y; z) ของจุดนี้จะเป็นไปตามความไม่เท่าเทียมกัน x 2 + y 2 + z 2 ≤4 เป็นเท่าใด
, จุดจะถูกกำหนดโดยการสุ่ม ความน่าจะเป็นที่พิกัด (x; y; z) ของจุดนี้จะเป็นไปตามความไม่เท่าเทียมกัน x 2 + y 2 + z 2 ≤4 เป็นเท่าใด
คำตอบ: 1/3.
4.12. จุดถูกโยนเข้าไปในสี่เหลี่ยมผืนผ้าที่มีจุดยอด R(-2;0), L(-2;9), M (4;9), N (4;0) ค้นหาความน่าจะเป็นที่พิกัดของมันจะตอบสนองความไม่เท่าเทียมกัน 0 ≤ y ≤ 2x – x 2 +8
คำตอบ: 2/3
4.13. พื้นที่ G ล้อมรอบด้วยวงกลม x 2 + y 2 = 25 และบริเวณ g ล้อมรอบด้วยวงกลมนี้และพาราโบลา 16x - 3y 2 > 0 จงหาความน่าจะเป็นที่จะตกไปยังพื้นที่ g
คำตอบ: ≈ 0;346.
4.14. สุ่มจำนวนบวก x และ y สองตัว โดยแต่ละจำนวนไม่เกินหนึ่งตัว จงหาความน่าจะเป็นที่ผลรวม x + y ไม่เกิน 1 และผลิตภัณฑ์ x · y ไม่น้อยกว่า 0.09
คำตอบ: ≈ 0;198.