Alapvető elemi függvények és tulajdonságaik. A függvények alapvető tulajdonságai

Az alapvető elemi funkciók teljes listája

Az alapvető elemi függvények osztálya a következőket tartalmazza:

1. $y=C$ konstans függvény, ahol a $C$ egy konstans. Egy ilyen függvény bármely $x$ esetén ugyanazt a $C$ értéket veszi fel.
2. $y=x^(a) $ hatványfüggvény, ahol az $a$ kitevő egy valós szám.
3. $y=a^(x) $ exponenciális függvény, ahol az alap $a>0$, $a\ne 1$ fok.
4. $y=\log _(a) x$ logaritmikus függvény, ahol a logaritmus alapja $a>0$, $a\ne 1$.
5. Trigonometrikus függvények $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ sec\,x$.
6. Inverz trigonometrikus függvények $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , x$.

Tápellátási funkciók

Figyelembe vesszük a $y=x^(a) $ hatványfüggvény viselkedését azokban a legegyszerűbb esetekben, amikor a kitevője egész szám hatványozását és gyökérkivonását határozza meg.

1. eset

A $y=x^(a) $ függvény kitevője egy természetes szám, azaz $y=x^(n) $, $n\in N$.

Ha $n=2\cdot k$ páros szám, akkor a $y=x^(2\cdot k) $ függvény páros és korlátlanul növekszik, mintha a $\left(x\to +\infty \ right argumentum )$, és ennek korlátlan csökkentésével $\left(x\to -\infty \right)$. A függvénynek ez a viselkedése a $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ és $\mathop(\lim )\ kifejezésekkel írható le limits_(x\to -\infty ) x^(2\cdot k) =+\infty $, ami azt jelenti, hogy a függvény mindkét esetben korlátlanul növekszik ($\lim $ a határ). Példa: $y=x^(2) $ függvény grafikonja.

Ha a $n=2\cdot k-1$ páratlan szám, akkor a $y=x^(2\cdot k-1) $ függvény páratlan, korlátlanul növekszik, ha az argumentum határozatlanul nő, és korlátlanul csökken, ha csökken határozatlan ideig. A függvénynek ez a viselkedése a $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ és $\mathop(\lim) kifejezésekkel írható le )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. Példa: $y=x^(3) $ függvény grafikonja.

2. eset

A $y=x^(a) $ függvény kitevője egy negatív egész szám, azaz $y=\frac(1)(x^(n) ) $, $n\in N$.

Ha $n=2\cdot k$ páros szám, akkor a $y=\frac(1)(x^(2\cdot k) ) $ függvény páros, és aszimptotikusan (fokozatosan) megközelíti a nullát, mint a korlátlan növekedés argumentum esetén , és annak korlátlan csökkenésével. A függvénynek ez a viselkedése egyetlen $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$ kifejezéssel írható le, ami azt jelenti, hogy az argumentum abszolút értékben való korlátlan növelésével a függvény határa nulla. Ezenkívül, mivel az argumentum mind a bal $\left(x\to 0-0\right)$, mind a jobb oldalon $\left(x\to 0+0\right)$ nullára hajlik, a függvény növekszik anélkül, hogy határ. Ezért a $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ és $\mathop(\lim )\ kifejezések limits_ érvényesek (x\-0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, ami azt jelenti, hogy a $y=\frac(1)(x^(2) függvény \cdot k ) ) $ mindkét esetben végtelen korlátja $+\infty $. Példa: $y=\frac(1)(x^(2) ) $ függvény grafikonja.

Ha a $n=2\cdot k-1$ páratlan szám, akkor a $y=\frac(1)(x^(2\cdot k-1) ) $ függvény páratlan, és aszimptotikusan nullához közelít, mintha mindkettő az argumentum korlátlanul növekszik és amikor csökken. A függvénynek ez a viselkedése egyetlen kifejezéssel írható le: $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$. Ráadásul, ahogy az argumentum a bal oldalon a nullához közelít, a függvény korlátlanul csökken, és ahogy az argumentum nullához közeledik a jobb oldalon, a függvény korlát nélkül növekszik, azaz $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ és $\mathop(\lim )\limits_(x\to 0+0) \frac(1)( x^(2\cdot k-1) ) =+\infty $. Példa: $y=\frac(1)(x) $ függvény grafikonja.

3. eset

A $y=x^(a) $ függvény kitevője a természetes szám inverze, azaz $y=\sqrt[(n)](x) $, $n\in N$.

Ha a $n=2\cdot k$ páros szám, akkor a $y=\pm \sqrt[(2\cdot k)](x) $ függvény kétértékű, és csak a $x\ge 0 esetén van megadva. $. Az argumentum korlátlan növelésével a $y=+\sqrt[(2\cdot k)](x) $ függvény értéke korlátlanul növekszik, és a $y=-\sqrt[(2\) cdot k)](x) $ korlátlanul csökken, azaz $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right )=+\infty $ és $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. Példa: $y=\pm \sqrt(x) $ függvény grafikonja.

Ha a $n=2\cdot k-1$ páratlan szám, akkor a $y=\sqrt[(2\cdot k-1)](x) $ függvény páratlan, és korlátlanul növekszik az argumentum korlátlan növekedésével és korlátlanul csökken, ha korlátlan, akkor csökken, azaz $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ és $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. Példa: $y=\sqrt[(3)](x) $ függvény grafikonja.

Exponenciális és logaritmikus függvények

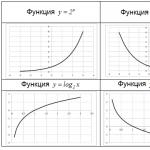
Az exponenciális $y=a^(x) $ és a logaritmikus $y=\log _(a) x$ függvények kölcsönösen inverzek. Gráfjaik szimmetrikusak az első és harmadik koordinátaszög közös felezőpontjához képest.

Amikor a $\left(x\to +\infty \right)$ argumentum korlátlanul növekszik, az exponenciális függvény vagy $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ korlátlanul növekszik, ha $a>1$, vagy aszimptotikusan megközelíti a nullát $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =0$, ha $a1$, vagy $\mathop korlát nélkül nő (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, ha $a

A $y=a^(x) $ függvény jellemző értéke a $x=0$. Ebben az esetben az összes exponenciális függvény, függetlenül az $a$-tól, szükségszerűen metszi a $Oy$ tengelyt $y=1$-ban. Példák: $y=2^(x) $ és $y = \left (\frac(1)(2) \right)^(x) $ függvények grafikonjai.

A $y=\log _(a) x$ logaritmikus függvény csak $x > 0$ esetén van definiálva.

Ahogy a $\left(x\to +\infty \right)$ argumentum korlátlanul növekszik, a logaritmikus függvény vagy a $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+ \ korlátlanul növekszik infty $, ha $a>1$, vagy korlátlanul csökken $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, ha $a1 $, vagy korlátozás nélkül $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $ növekszik, ha $a

A $y=\log _(a) x$ függvény jellemző értéke a $y=0$. Ebben az esetben minden logaritmikus függvény, függetlenül az $a$-tól, szükségszerűen metszi az $Ox$ tengelyt $x=1$-ban. Példák: $y=\log _(2) x$ és $y=\log _(1/2) x$ függvények grafikonjai.

Néhány logaritmikus függvénynek speciális jelölése van. Különösen, ha a logaritmus alapja $a=10$, akkor egy ilyen logaritmust decimálisnak nevezünk, és a megfelelő függvényt a következőképpen írjuk: $y=\lg x$. Ha pedig a $e=2,7182818\ldots $ irracionális számot választjuk a logaritmus alapjául, akkor az ilyen logaritmust természetesnek nevezzük, és a megfelelő függvényt a következőképpen írjuk fel: $y=\ln x$. Ennek inverze a kitevőnek nevezett $y=e^(x) $ függvény.

Alapvető elemi funkciók a következők: állandó függvény (konstans), gyök n-edik fok, hatványfüggvény, exponenciális, logaritmikus függvény, trigonometrikus és inverz trigonometrikus függvények.

Állandó funkció.

Az összes valós szám halmazán egy állandó függvényt adunk meg a képlettel, ahol C– valami valós szám. Egy konstans függvény hozzárendeli a független változó minden aktuális értékét x a függő változó azonos értéke y- jelentése VAL VEL. Az állandó függvényt konstansnak is nevezik.

A konstans függvény grafikonja az x tengellyel párhuzamos, a koordinátákkal ellátott ponton áthaladó egyenes (0,C). Például mutassuk meg a konstans függvények grafikonjait y=5,y=-2és , amelyek az alábbi ábrán a fekete, piros és kék vonalaknak felelnek meg.

Egy állandó függvény tulajdonságai.

Domain: a valós számok teljes halmaza.

Az állandó függvény páros.

Értéktartomány: egyes számból álló halmaz VAL VEL.

Az állandó függvény nem növekvő és nem csökkenő (ezért állandó).

Nincs értelme konvexitásról és konkávságról beszélni.

Nincsenek aszimptoták.

A függvény áthalad a ponton (0,C) Koordináta sík.

Az n-edik fok gyökere.

Tekintsük az alapvető elemi függvényt, amelyet a képlet ad meg, ahol n– egynél nagyobb természetes szám.

Az n-edik gyök, n páros szám.

Kezdjük a gyökérfüggvénnyel n-edik hatvány a gyökkitevő páros értékeire n.

Példaként álljon itt egy kép a függvénygrafikonok képeivel és , ezek fekete, piros és kék vonalaknak felelnek meg.

A páros fokú gyökfüggvények grafikonjai hasonló megjelenésűek a kitevő más értékeinél.

A gyökérfüggvény tulajdonságain -edik hatalom az egyenletesn .

Az n-edik gyök, n páratlan szám.

Root funkció n-edik hatvány páratlan gyökkitevővel n a valós számok teljes halmazán van definiálva. Például itt vannak a függvénygrafikonok és , ezek a fekete, piros és kék görbéknek felelnek meg.

1) Funkciótartomány és függvénytartomány.

Egy függvény tartománya az összes érvényes érvényes argumentumérték halmaza x(változó x), amelyhez a függvény y = f(x) eltökélt. Egy függvény tartománya az összes valós érték halmaza y, amelyet a függvény elfogad.

Az elemi matematikában a függvényeket csak valós számok halmazán tanulmányozzák.

2) Funkció nullák.

A nulla függvény annak az argumentumnak az értéke, amelynél a függvény értéke nulla.

3) Egy függvény állandó előjelének intervallumai.

A függvény állandó előjelének intervallumai olyan argumentumértékek halmazai, amelyeken a függvényértékek csak pozitívak vagy csak negatívak.

4) A függvény monotonitása.

Növekvő függvény (egy bizonyos intervallumban) olyan függvény, amelyben ebből az intervallumból származó argumentum nagyobb értéke a függvény nagyobb értékének felel meg.

Csökkenő függvény (egy bizonyos intervallumban) olyan függvény, amelyben ebből az intervallumból származó argumentum nagyobb értéke a függvény kisebb értékének felel meg.

5) Páros (páratlan) függvény.

A páros függvény olyan függvény, amelynek definíciós tartománya szimmetrikus az origóhoz és bármely függvényhez x a definíció tartományából az egyenlőség f(-x) = f(x). A páros függvény grafikonja szimmetrikus az ordinátára.

A páratlan függvény olyan függvény, amelynek definíciós tartománya szimmetrikus az origóhoz és bármely függvényhez x a definíció tartományából az egyenlőség igaz f(-x) = - f(x). Egy páratlan függvény grafikonja szimmetrikus az origóra.

6) Korlátozott és korlátlan funkciók.

Egy függvényt korlátosnak nevezünk, ha van olyan pozitív M szám, amelyre |f(x)| ≤ M x összes értékére. Ha ilyen szám nem létezik, akkor a függvény korlátlan.

7) A függvény periodicitása.

Egy f(x) függvény periodikus, ha van egy nullától eltérő T szám, amelyre a függvény definíciós tartományából származó bármely x-re teljesül a következő: f(x+T) = f(x). Ezt a legkisebb számot a függvény periódusának nevezzük. Minden trigonometrikus függvény periodikus. (Trigonometrikus képletek).

19. Alapvető elemi függvények, tulajdonságaik és grafikonjai. Függvények alkalmazása a közgazdaságtanban.

Alapvető elemi funkciók. Tulajdonságaik és grafikonjaik

1. Lineáris függvény.

Lineáris függvény alakú függvénynek nevezzük, ahol x változó, a és b valós számok.

Szám A az egyenes meredekségének nevezzük, ez egyenlő ezen egyenes dőlésszögének az x tengely pozitív irányához viszonyított érintőjével. A lineáris függvény grafikonja egy egyenes. Két pont határozza meg.

Lineáris függvény tulajdonságai

1. Definíciós tartomány - az összes valós szám halmaza: D(y)=R

2. Az értékkészlet az összes valós szám halmaza: E(y)=R

3. A függvény nulla értéket vesz fel, ha vagy.

4. A függvény növekszik (csökken) a teljes definíciós tartományban.

5. Egy lineáris függvény folytonos a teljes definíciós tartományban, differenciálható és .

2. Másodfokú függvény.

Egy olyan alakú függvényt, ahol x változó, a, b, c együtthatók valós számok, ún. négyzetes.

Egy összetett változó függvényeit tekintve Liouville valamivel tágabban határozta meg az elemi függvényeket. Elemi funkció y változó x- analitikus függvény, amely algebrai függvényeként ábrázolható xés funkciókat , és valamilyen algebrai függvény logaritmusa vagy kitevője g 1-től x .

Például a bűn ( x) - algebrai függvénye e énx .

A megfontolás általánosságának korlátozása nélkül tekinthetjük a függvényeket algebrailag függetlennek, vagyis ha az algebrai egyenlet mindenre teljesül. x, akkor a polinom összes együtthatója egyenlők nullával.

Az elemi függvények differenciálása

Ahol z 1 "(z) egyenlő vagy g 1 " / g 1 ill z 1 g 1" attól függően, hogy logaritmusról van-e szó z 1 vagy exponenciális stb. A gyakorlatban célszerű derivált táblát használni.

Elemi funkciók integrálása

Liouville tétele az alapja az elemi függvények szimbolikus integrálására szolgáló algoritmusok létrehozásának, amelyeket pl.

A határértékek kiszámítása

Liouville elmélete nem alkalmazható a határértékek kiszámítására. Nem tudni, hogy létezik-e olyan algoritmus, amely egy elemi képlettel adott sorozatra választ ad, hogy van-e határértéke vagy sem. Például nyitott a kérdés, hogy a sorozat konvergál-e.

Irodalom

• J. Liouville. Mémoire sur l'intégration d'une classe de fonctions transcendantes// J. Reine Angew. Math. Bd. 13. o. 93-118. (1835)
• J.F. Ritt. Integráció véges feltételekben. N.-Y., 1949 // http://lib.homelinux.org
• A. G. Khovansky. Topológiai Galois elmélet: egyenletek megoldhatósága és megoldhatatlansága véges formában Ch. 1. M, 2007

Megjegyzések

Wikimédia Alapítvány. 2010.

• Elemi gerjesztés
• Elemi eredmény

Nézze meg, mi az „elemi függvény” más szótárakban:

elemi funkció- Olyan függvény, amely kisebb funkciókra bontva nem határozható meg egyértelműen a digitális átviteli hierarchiában. Ezért a hálózat szempontjából oszthatatlan (ITU T G.806). Témakörök: telekommunikáció, alapfogalmak EN adaptációs funkcióA... Műszaki fordítói útmutató

a hálózati szintek közötti interakció funkciója- Egy elemi funkció, amely a jellemző információk interakcióját biztosítja két hálózati réteg között. (ITU T G.806). Témák: telekommunikáció, az EN réteg alapfogalmai... ... Műszaki fordítói útmutató