Trouver l'angle entre les équations directes données. Angle entre les lignes

Définition. Si deux lignes sont données y = k 1 x + b 1 , y = k 2 x + b 2 , alors l'angle aigu entre ces lignes sera défini comme

Deux droites sont parallèles si k 1 = k 2 . Deux droites sont perpendiculaires si k 1 = -1/ k 2 .

Théorème. Les droites Ax + Vy + C \u003d 0 et A 1 x + B 1 y + C 1 \u003d 0 sont parallèles lorsque les coefficients A 1 \u003d λA, B 1 \u003d λB sont proportionnels. Si aussi С 1 = λС, alors les droites coïncident. Les coordonnées du point d'intersection de deux droites sont trouvées comme solution du système d'équations de ces droites.

Équation d'une droite passant par un point donné

Perpendiculaire à cette ligne

Définition. La ligne passant par le point M 1 (x 1, y 1) et perpendiculaire à la ligne y \u003d kx + b est représentée par l'équation :

Distance d'un point à une ligne

Théorème. Si un point M(x 0, y 0) est donné, alors la distance à la ligne Ax + Vy + C \u003d 0 est définie comme

.

Preuve. Soit le point M 1 (x 1, y 1) la base de la perpendiculaire laissée tomber du point M à une droite donnée. Alors la distance entre les points M et M 1 :

(1)

Les coordonnées x 1 et y 1 peuvent être trouvées comme solution du système d'équations :

La deuxième équation du système est l'équation d'une droite passant par un point donné M 0 perpendiculaire à une droite donnée. Si nous transformons la première équation du système sous la forme :

A(x - x 0) + B(y - y 0) + Ax 0 + Par 0 + C = 0,

puis, en résolvant, on obtient :

En remplaçant ces expressions dans l'équation (1), on trouve :

Le théorème a été démontré.

Exemple. Déterminez l'angle entre les lignes : y = -3 x + 7 ; y = 2 x + 1.

k 1 \u003d -3; k2 = 2 ; tgφ = ; φ= p /4.

Exemple. Montrer que les droites 3x - 5y + 7 = 0 et 10x + 6y - 3 = 0 sont perpendiculaires.

Décision. Nous trouvons: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, donc les lignes sont perpendiculaires.

Exemple. Les sommets du triangle A(0; 1), B (6; 5), C (12; -1) sont donnés. Trouvez l'équation de la hauteur tirée du sommet C.

Décision. On trouve l'équation du côté AB : ; 4 x = 6 y - 6 ;

2x – 3y + 3 = 0 ;

L'équation de hauteur souhaitée est : Ax + By + C = 0 ou y = kx + b. k = . Alors y = . Car hauteur passe par le point C, alors ses coordonnées satisfont cette équation: d'où b = 17. Total : .

Réponse : 3x + 2a - 34 = 0.

Équation d'une droite passant par un point donné dans une direction donnée. Équation d'une droite passant par deux points donnés. Angle entre deux lignes. Condition de parallélisme et de perpendicularité de deux droites. Détermination du point d'intersection de deux lignes

1. Équation d'une droite passant par un point donné UN(X 1 , y 1) dans une direction donnée, déterminée par la pente k,

y - y 1 = k(X - X 1). (1)

Cette équation définit un faisceau de droites passant par un point UN(X 1 , y 1), appelé centre du faisceau.

2. Équation d'une droite passant par deux points : UN(X 1 , y 1) et B(X 2 , y 2) s'écrit ainsi :

La pente d'une droite passant par deux points donnés est déterminée par la formule

3. Angle entre droites UN et B est l'angle de rotation de la première droite UN autour du point d'intersection de ces lignes dans le sens antihoraire jusqu'à ce qu'il coïncide avec la deuxième ligne B. Si deux droites sont données par des équations de pente

y = k 1 X + B 1 ,

y = k 2 X + B 2 , (4)

alors l'angle entre eux est déterminé par la formule

Il convient de noter qu'au numérateur de la fraction, la pente de la première droite est soustraite de la pente de la deuxième droite.

Si les équations d'une droite sont données dans vue générale

UN 1 X + B 1 y + C 1 = 0,

UN 2 X + B 2 y + C 2 = 0, (6)

l'angle entre eux est déterminé par la formule

4. Conditions de parallélisme de deux lignes :

a) Si les droites sont données par les équations (4) avec une pente, alors la condition nécessaire et suffisante de leur parallélisme est l'égalité de leurs pentes :

k 1 = k 2 . (8)

b) Pour le cas où les droites sont données par des équations sous forme générale (6), la condition nécessaire et suffisante pour leur parallélisme est que les coefficients aux coordonnées courantes correspondantes dans leurs équations soient proportionnels, c'est-à-dire

5. Conditions de perpendicularité de deux lignes :

a) Dans le cas où les droites sont données par les équations (4) avec une pente, la condition nécessaire et suffisante de leur perpendicularité est qu'elles facteurs de pente sont de grandeur réciproque et de signe opposé, c'est-à-dire

Cette condition peut aussi s'écrire sous la forme

k 1 k 2 = -1. (11)

b) Si les équations des droites sont données sous la forme générale (6), alors la condition de leur perpendicularité (nécessaire et suffisante) est de vérifier l'égalité

UN 1 UN 2 + B 1 B 2 = 0. (12)

6. Les coordonnées du point d'intersection de deux droites sont trouvées en résolvant le système d'équations (6). Les droites (6) se coupent si et seulement si

1. Ecrire les équations des droites passant par le point M, dont l'une est parallèle et l'autre perpendiculaire à la droite donnée l.

coin entre des lignes droites dans l'espace, nous appellerons l'un quelconque des angles adjacents formés par deux lignes droites tracées par un point arbitraire parallèle aux données.

Soit deux droites données dans l'espace :

Évidemment, l'angle φ entre les lignes peut être pris comme l'angle entre leurs vecteurs directeurs et . Puisque , alors selon la formule du cosinus de l'angle entre les vecteurs nous obtenons

Les conditions de parallélisme et de perpendicularité de deux droites sont équivalentes aux conditions de parallélisme et de perpendicularité de leurs vecteurs directeurs et :

Deux droites sont parallèles si et seulement si leurs coefficients respectifs sont proportionnels, c'est-à-dire je 1 parallèle je 2 si et seulement si parallèle .

Deux droites perpendiculaire si et seulement si la somme des produits des coefficients correspondants est égale à zéro : .

À but entre ligne et avion

Laisse la ligne ré- non perpendiculaire au plan θ ;
ré′− projection d'une droite ré au plan θ ;
Le plus petit des angles entre des droites ré et ré′ nous appellerons angle entre droite et plan.
Notons-le comme φ=( ré,θ)
Si un ré⊥θ , alors ( ré,θ)=π/2

Oi→j→k→− système de coordonnées rectangulaires.
Équation du plan :

θ: Hache+Par+cz+ré=0

On considère que la droite est donnée par un point et un vecteur directeur : ré[M 0,p→]
Vecteur n→(UN,B,C)⊥θ
Il reste alors à trouver l'angle entre les vecteurs n→ et p→, notons-le γ=( n→,p→).

Si l'angle γ<π/2 , то искомый угол φ=π/2−γ .

Si l'angle γ>π/2 , alors l'angle requis φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Puis, angle entre droite et plan peut être calculé à l'aide de la formule :

sinφ=∣cosγ∣=∣ ∣ App 1+pb 2+CP 3∣ ∣ √UN 2+B 2+C 2√p 21+p 22+p 23

Question 29. Le concept d'une forme quadratique. La définition de signe des formes quadratiques.

Forme quadratique j (x 1, x 2, ..., x n) n variables réelles x 1, x 2, ..., x n s'appelle une somme de la forme
, (1)

où aij sont des nombres appelés coefficients. Sans perte de généralité, on peut supposer que aij = un ji.

La forme quadratique s'appelle valide, si aij О GR. Matrice de forme quadratique est appelée la matrice composée de ses coefficients. La forme quadratique (1) correspond à une matrice symétrique unique
c'est à dire. UNE T = UNE. Par conséquent, la forme quadratique (1) peut être écrite sous forme matricielle j ( X) = x T Ah, où xT = (X 1 X 2 … xn). (2)

Et inversement, toute matrice symétrique (2) correspond à une forme quadratique unique à la notation des variables près.

Le rang de la forme quadratique est appelé le rang de sa matrice. La forme quadratique s'appelle non dégénéré, si sa matrice est non singulière MAIS. (rappelons que la matrice MAIS est dit non dégénéré si son déterminant n'est pas zéro). Sinon, la forme quadratique est dégénérée.

définie positive(ou strictement positif) si

je ( X) > 0 , pour tout le monde X = (X 1 , X 2 , …, xn), Outre X = (0, 0, …, 0).

Matrice MAIS forme quadratique définie positive j ( X) est aussi appelé défini positif. Par conséquent, une forme quadratique définie positive correspond à une matrice définie positive unique et vice versa.

La forme quadratique (1) est appelée défini négatif(ou strictement négatif) si

je ( X) < 0, для любого X = (X 1 , X 2 , …, xn), Outre X = (0, 0, …, 0).

De même que ci-dessus, une matrice quadratique définie négative est également appelée négative définie.

Par conséquent, une forme quadratique définie positivement (négativement) j ( X) atteint la valeur minimale (maximale) j ( X*) = 0 pour X* = (0, 0, …, 0).

Notez que la plupart des formes quadratiques ne sont pas définies par le signe, c'est-à-dire qu'elles ne sont ni positives ni négatives. De telles formes quadratiques disparaissent non seulement à l'origine du système de coordonnées, mais aussi en d'autres points.

Lorsque n> 2, des critères spéciaux sont nécessaires pour vérifier la définition du signe d'une forme quadratique. Considérons-les.

Mineurs majeurs forme quadratique sont appelés mineurs :

c'est-à-dire qu'il s'agit de mineurs de rang 1, 2, …, n matrices MAIS situé à gauche coin supérieur, le dernier d'entre eux coïncide avec le déterminant de la matrice MAIS.

Critère de définition positive (Critère de Sylvester)

X) = x T Ah est définie positive, il faut et il suffit que tous les principaux mineurs de la matrice MAISétaient positifs, c'est-à-dire : M 1 > 0, M 2 > 0, …, M n > 0. Critère de certitude négative Pour la forme quadratique j ( X) = x T Ah est définie négative, il faut et il suffit que ses principaux mineurs d'ordre pair soient positifs, et ceux d'ordre impair soient négatifs, soit : M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

ANGLE ENTRE PLANS

Considérons deux plans α 1 et α 2 donnés respectivement par les équations :

En dessous de coin entre deux plans on comprendra l'un des angles dièdres formés par ces plans. Il est évident que l'angle entre les vecteurs normaux et les plans α 1 et α 2 est égal à l'un des angles dièdres adjacents indiqués ou . Alors . Car et , alors

.

Exemple. Déterminer l'angle entre les plans X+2y-3z+4=0 et 2 X+3y+z+8=0.

Condition de parallélisme de deux plans.

Deux plans α 1 et α 2 sont parallèles si et seulement si leurs vecteurs normaux et sont parallèles, et donc .

Ainsi, deux plans sont parallèles si et seulement si les coefficients aux coordonnées correspondantes sont proportionnels :

ou alors

Condition de perpendicularité des plans.

Il est clair que deux plans sont perpendiculaires si et seulement si leurs vecteurs normaux sont perpendiculaires, et donc, ou .

Ainsi, .

Exemples.

DIRECT DANS L'ESPACE.

ÉQUATION VECTORIELLE DIRECTE.

ÉQUATIONS PARAMÉTRIQUES DIRECTES

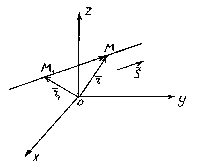
La position d'une ligne droite dans l'espace est complètement déterminée en spécifiant l'un de ses points fixes M 1 et un vecteur parallèle à cette droite.

Un vecteur parallèle à une droite est appelé guidage le vecteur de cette droite.

Alors laisse tomber je passe par un point M 1 (X 1 , y 1 , z 1) se trouvant sur une droite parallèle au vecteur .

Considérons un point arbitraire M(x,y,z) sur une ligne droite. On peut voir sur la figure que .

Les vecteurs et sont colinéaires, il existe donc un tel nombre t, quoi , où est le multiplicateur t peut prendre n'importe quelle valeur numérique en fonction de la position du point M sur une ligne droite. Facteur t est appelé un paramètre. Dénotant les vecteurs de rayon des points M 1 et M respectivement, par et , on obtient . Cette équation s'appelle vecteuréquation de droite. Il montre que chaque valeur de paramètre t correspond au rayon vecteur d'un point M allongé sur une ligne droite.

Nous écrivons cette équation sous forme de coordonnées. Remarquerez que , et d'ici

Les équations résultantes sont appelées paramétriqueéquations de droite.

Lors de la modification du paramètre t changement de coordonnées X, y et z et point M se déplace en ligne droite.

ÉQUATIONS CANONIQUES DIRECTES

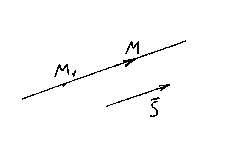
Laisser être M 1 (X 1 , y 1 , z 1) - un point situé sur une droite je, et est son vecteur directeur. Encore une fois, prenez un point arbitraire sur une droite M(x,y,z) et considérons le vecteur .

Il est clair que les vecteurs et sont colinéaires, donc leurs coordonnées respectives doivent être proportionnelles, d'où

– canoniqueéquations de droite.

Remarque 1. A noter que les équations canoniques de la droite pourraient être obtenues à partir des équations paramétriques en éliminant le paramètre t. En effet, à partir des équations paramétriques on obtient ou alors .

Exemple.Écrire l'équation d'une droite de manière paramétrique.

Dénoter , Par conséquent X = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remarque 2. Laissez la ligne être perpendiculaire à l'un des axes de coordonnées, par exemple, l'axe Bœuf. Alors le vecteur directeur de la droite est perpendiculaire Bœuf, Par conséquent, m=0. Par conséquent, les équations paramétriques de la droite prennent la forme

Éliminer le paramètre des équations t, on obtient les équations de la droite sous la forme

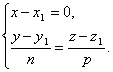
Cependant, dans ce cas aussi, on convient d'écrire formellement les équations canoniques de la droite sous la forme . Ainsi, si le dénominateur de l'une des fractions est zéro, cela signifie que la ligne est perpendiculaire à l'axe de coordonnées correspondant.

De même, les équations canoniques correspond à une droite perpendiculaire aux axes Bœuf et Oy ou axe parallèle onces.

Exemples.

ÉQUATIONS GÉNÉRALES UNE LIGNE DIRECTE COMME LIGNE D'INTERCEPTION DE DEUX PLANS

Par chaque ligne droite dans l'espace passe un nombre infini de plans. Deux d'entre eux, se croisant, le définissent dans l'espace. Par conséquent, les équations de deux de ces plans, considérés ensemble, sont les équations de cette droite.

En général, deux plans non parallèles donnés par les équations générales

déterminer leur ligne d'intersection. Ces équations sont appelées équations générales droit.

Exemples.

Construire une droite donnée par des équations

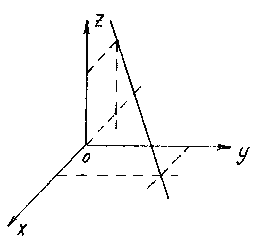
Pour construire une droite, il suffit de trouver deux de ses points. Le plus simple est de choisir les points d'intersection de la ligne avec les plans de coordonnées. Par exemple, le point d'intersection avec le plan xOy on obtient à partir des équations d'une droite, en supposant z= 0:

En résolvant ce système, on trouve le point M 1 (1;2;0).

De même, en supposant y= 0, on obtient le point d'intersection de la droite avec le plan xOz:

A partir des équations générales d'une droite, on peut passer à ses équations canoniques ou paramétriques. Pour ce faire, vous devez trouver un point M 1 sur la droite et le vecteur directeur de la droite.

Coordonnées des points M 1 on obtient de ce système d'équations, en donnant à l'une des coordonnées une valeur arbitraire. Pour trouver le vecteur directeur, notez que ce vecteur doit être perpendiculaire aux deux vecteurs normaux et . Donc, pour le vecteur directeur de la droite je vous pouvez prendre le produit croisé de vecteurs normaux :

.

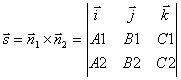Exemple. Donner les équations générales de la droite à la forme canonique.

Trouver un point sur une droite. Pour ce faire, nous choisissons arbitrairement l'une des coordonnées, par exemple, y= 0 et résoudre le système d'équations :

Les vecteurs normaux des plans définissant la droite ont pour coordonnées Par conséquent, le vecteur de direction sera droit

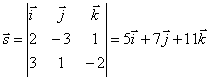. Ainsi, je: .

ANGLE ENTRE DROITS

coin entre des lignes droites dans l'espace, nous appellerons l'un quelconque des angles adjacents formés par deux lignes droites tracées par un point arbitraire parallèle aux données.

Soit deux droites données dans l'espace :

Évidemment, l'angle φ entre les lignes peut être pris comme l'angle entre leurs vecteurs directeurs et . Puisque , alors selon la formule du cosinus de l'angle entre les vecteurs nous obtenons

Je serai bref. L'angle entre deux droites est égal à l'angle entre leurs vecteurs directeurs. Ainsi, si vous parvenez à trouver les coordonnées des vecteurs directeurs a \u003d (x 1; y 1; z 1) et b \u003d (x 2; y 2; z 2), vous pouvez trouver l'angle. Plus précisément, le cosinus de l'angle selon la formule :

Voyons comment cette formule fonctionne sur des exemples spécifiques :

Tâche. Les points E et F sont marqués dans le cube ABCDA 1 B 1 C 1 D 1 - les milieux des arêtes A 1 B 1 et B 1 C 1, respectivement. Trouver l'angle entre les droites AE et BF.

Puisque l'arête du cube n'est pas spécifiée, nous fixons AB = 1. Nous introduisons un système de coordonnées standard : l'origine est au point A et les axes x, y, z sont dirigés le long de AB, AD et AA 1, respectivement . Le segment unitaire est égal à AB = 1. Trouvons maintenant les coordonnées des vecteurs directeurs de nos droites.

Trouver les coordonnées du vecteur AE. Pour ce faire, nous avons besoin des points A = (0 ; 0 ; 0) et E = (0,5 ; 0 ; 1). Le point E étant le milieu du segment A 1 B 1 , ses coordonnées sont égales à la moyenne arithmétique des coordonnées des extrémités. Notez que l'origine du vecteur AE coïncide avec l'origine, donc AE = (0,5 ; 0 ; 1).

Passons maintenant au vecteur BF. De même, on analyse les points B = (1 ; 0 ; 0) et F = (1 ; 0,5 ; 1), car F - le milieu du segment B 1 C 1 . Nous avons:
BF = (1 - 1 ; 0,5 - 0 ; 1 - 0) = (0 ; 0,5 ; 1).

Ainsi, les vecteurs de direction sont prêts. Le cosinus de l'angle entre les droites est le cosinus de l'angle entre les vecteurs directeurs, on a donc :

Tâche. Dans un prisme trièdre régulier ABCA 1 B 1 C 1 , dont toutes les arêtes sont égales à 1, les points D et E sont marqués - les milieux des arêtes A 1 B 1 et B 1 C 1, respectivement. Trouver l'angle entre les droites AD et BE.

Nous introduisons un système de coordonnées standard : l'origine est au point A, l'axe x est dirigé selon AB, z - selon AA 1 . Nous orientons l'axe y de sorte que le plan OXY coïncide avec le plan ABC. Le segment unitaire est égal à AB = 1. Trouvez les coordonnées des vecteurs directeurs pour les lignes souhaitées.

Trouvons d'abord les coordonnées du vecteur AD. Considérons les points : A = (0 ; 0 ; 0) et D = (0,5 ; 0 ; 1), car D - le milieu du segment A 1 B 1 . Comme le début du vecteur AD coïncide avec l'origine, on obtient AD = (0,5 ; 0 ; 1).

Trouvons maintenant les coordonnées du vecteur BE. Le point B = (1 ; 0 ; 0) est facile à calculer. Avec le point E - le milieu du segment C 1 B 1 - un peu plus difficile. Nous avons:

Il reste à trouver le cosinus de l'angle :

Tâche. Dans un prisme hexagonal régulier ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , dont toutes les arêtes sont égales à 1, les points K et L sont marqués - les milieux des arêtes A 1 B 1 et B 1 C 1, respectivement. Trouver l'angle entre les droites AK et BL.

Nous introduisons un système de coordonnées standard pour un prisme : nous plaçons l'origine des coordonnées au centre de la base inférieure, dirigeons l'axe des x le long de FC, l'axe des y passant par les milieux des segments AB et DE, et l'axe des z verticalement vers le haut. Le segment unitaire est à nouveau égal à AB = 1. Notons les coordonnées des points qui nous intéressent :

Les points K et L sont les milieux des segments A 1 B 1 et B 1 C 1, respectivement, de sorte que leurs coordonnées sont trouvées par la moyenne arithmétique. Connaissant les points, on trouve les coordonnées des vecteurs directeurs AK et BL :

Trouvons maintenant le cosinus de l'angle :

Tâche. Dans le droit pyramide quadrangulaire SABCD, dont toutes les arêtes sont égales à 1, les points E et F sont marqués - les milieux des côtés SB et SC, respectivement. Trouver l'angle entre les droites AE et BF.

Nous introduisons un système de coordonnées standard : l'origine est au point A, les axes x et y sont dirigés respectivement selon AB et AD, et l'axe z est dirigé verticalement vers le haut. Le segment unitaire est égal à AB = 1.

Les points E et F sont les milieux des segments SB et SC, respectivement, de sorte que leurs coordonnées sont trouvées comme la moyenne arithmétique des extrémités. Nous notons les coordonnées des points qui nous intéressent:
A = (0; 0; 0); B = (1 ; 0 ; 0)

Connaissant les points, on trouve les coordonnées des vecteurs directeurs AE et BF :

Les coordonnées du vecteur AE coïncident avec les coordonnées du point E, puisque le point A est l'origine. Il reste à trouver le cosinus de l'angle :