Направляющим вектором прямой l называется всякий ненулевой вектор (m , n ), параллельный этой прямой.

Пусть заданы точка M 1 (x 1 , y 1) и направляющий вектор (m , n ), тогда уравнение прямой, проходящей через точку M 1 в направлении вектора имеет вид: . Это уравнение называется каноническим уравнением прямой.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. Запишем каноническое уравнение прямой , преобразуем его. Получим х + у - 3 = 0

Уравнение прямой, проходящей через две точки

Пусть на плоскости заданы две точки M 1 (x 1 , y 1) и M 2 (x 2, y 2), тогда уравнение прямой, проходящей через эти точки имеет вид: . Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Применяя записанную выше формулу, получаем: ,

Уравнение прямой по точке и угловому коэффициенту

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду: и обозначить , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.

Уравнение прямой в отрезках

Если в общем уравнении прямой Ах + Ву + С = 0 коэффициент С ¹ 0, то, разделив на С, получим: или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох , а b – координатой точки пересечения прямой с осью Оу .

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках. А = -1, В = 1, С = 1, тогда а = -1, b = 1. Уравнение прямой в отрезках примет вид .

Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: ;

4x = 6y – 6; 2x – 3y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b .

k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3x + 2y – 34 = 0.

Практическое занятие №7

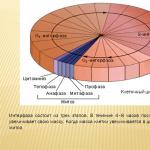
Наименование занятия: Кривые второго порядка.

Цель занятия: Научиться составлять кривых 2-го порядка, строить их.

Подготовка к занятию: Повторить теоретический материал по теме «Кривые 2-го порядка»

Литература:

1. Дадаян А.А. «Математика», 2004г.

Задание на занятие:

Порядок проведения занятия:

1. Получить допуск к работе
2. Выполнить задания
3. Ответить на контрольные вопросы.

1. Наименование, цель занятия, задание;
2. Выполненное задание;
3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Дать определение кривых второго порядка (окружности, эллипса, гиперболы, параболы), записать их канонические уравнения.
2. Что называется эксцентриситетом эллипса, гиперболы? Как его найти?
3. Записать уравнение равносторонней гиперболы

ПРИЛОЖЕНИЕ

Окружностью называется множество всех точек плоскости, равноудаленных от одной точки, называемой центром.

Пусть центром окружности является точка О (a; b ), а расстояние до любой точки М (х;у ) окружности равно R . Тогда (x – a ) 2 + (y – b ) 2 = R 2 – каноническое уравнение окружности с центром О (a; b ) и радиусом R.

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде: 2x 2 + 2y 2 – 8x + 5y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к каноническому виду. Для этого выделим полные квадраты:

x 2 + y 2 – 4x + 2,5y – 2 = 0

x 2 – 4x + 4 – 4 + y 2 + 2,5y + 25/16 – 25/16 – 2 = 0

(x – 2) 2 + (y + 5/4) 2 – 25/16 – 6 = 0

(x – 2) 2 + (y + 5/4) 2 = 121/16

Отсюда находим координаты центра О (2; -5/4); радиус R = 11/4.

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная, большая, чем расстояние между фокусами.

Фокусы обозначаются буквами F 1 , F с , сумма расстояний от любой точки эллипса до фокусов – 2а (2а > 2c ), a – большая полуось; b – малая полуось.

Каноническое уравнение эллипса имеет вид: , где a , b и c связаны между собой равенствами: a 2 – b 2 = c 2 (или b 2 – a 2 = c 2).

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к длине большей оси и называется эксцентриситетом. или .

Т.к. по определению 2а > 2c , то эксцентриситет всегда выражается правильной дробью, т.е. .

Пример. Составить уравнение эллипса, если его фокусы F 1 (0; 0), F 2 (1; 1), большая ось равна 2.

Уравнение эллипса имеет вид: .

Расстояние между фокусами: 2c = , таким образом, a 2 – b 2 = c 2 = . По условию 2а = 2, следовательно, а = 1, b = Искомое уравнение эллипса примет вид: .

Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Каноническое уравнение гиперболы имеет вид: или , где a , b и c связаны между собой равенством a 2 + b 2 = c 2 . Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Фокусы обозначаются буквами F 1 , F 2 , расстояние между фокусами – 2с , разность расстояний от любой точки гиперболы до фокусов – 2а (2а < 2c ). Ось 2а называется действительной осью гиперболы, ось 2b – мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси: или . Т.к. по определению 2а < 2c , то эксцентриситет гиперболы всегда выражается неправильной дробью, т.е. .

Если длина действительной оси равна длине мнимой оси, т.е. а = b , ε = , то гипербола называется равносторонней .

Пример. Составить каноническое уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением

Находим фокусное расстояние c 2 = 25 – 9 = 16.

Для гиперболы: c 2 = a 2 + b 2 = 16, ε = c/a = 2; c = 2a ; c 2 = 4a 2 ; a 2 = 4; b 2 = 16 – 4 = 12.

Тогда - искомое уравнение гиперболы.

Параболой называется множество точек плоскости, равноудаленных от заданной точки, называемой фокусом, и данной прямой, называемой директрисой.

Фокус параболы обозначается буквой F , директриса – d , расстояние от фокуса до директрисы – р .

Каноническое уравнение параболы, фокус которой расположен на оси абсцисс, имеет вид:

y 2 = 2px или y 2 = -2px

x = -p /2, x = p /2

Каноническое уравнение параболы, фокус которой расположен на оси ординат, имеет вид:

х 2 = 2pу или х 2 = -2pу

Уравнения директрис соответственно у = -p /2, у = p /2

Пример. На параболе у 2 = 8х найти точки, расстояние которой от директрисы равно 4.

Из уравнения параболы получаем, что р = 4. r = x + p /2 = 4; следовательно:

x = 2; y 2 = 16; y = ±4. Искомые точки: M 1 (2; 4), M 2 (2; -4).

Практическое занятие №8

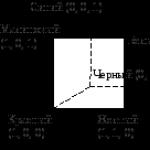
Наименование занятия: Действия над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел .

Цель занятия: Научиться выполнять действия над комплексными числами.

Подготовка к занятию: Повторить теоретический материал по теме «Комплексные числа».

Литература:

1. Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.

Задание на занятие:

1. Вычислить:

1) i 145 + i 147 + i 264 + i 345 + i 117 ;

2) (i 64 + i 17 + i 13 + i 82)·(i 72 – i 34);

Пусть прямая проходит через точки М 1 (х 1 ; у 1) и М 2 (х 2 ; у 2). Уравнение прямой, проходящей через точку М 1 , имеет вид у- у 1 = k (х - х 1), (10.6)

где k - пока неизвестный коэффициент.

Так как прямая проходит через точку М 2 (х 2 у 2), то координаты этой точки должны удовлетворять уравнению (10.6): у 2 -у 1 = k (х 2 -х 1).

Отсюда находим Подставляя найденное значениеk в уравнение (10.6), получим уравнение прямой, проходящей через точки М 1 и М 2:

Предполагается, что в этом уравнении х 1 ≠ х 2 , у 1 ≠ у 2

Если х 1 = х 2 , то прямая, проходящая через точки М 1 (х 1 ,у I) и М 2 (х 2 ,у 2) параллельна оси ординат. Ее уравнение имеет вид х = х 1 .

Если у 2 = у I , то уравнение прямой может быть записано в виде у = у 1 , прямая М 1 М 2 параллельна оси абсцисс.

Уравнение прямой в отрезках

Пусть прямая пересекает ось Ох в точке М 1 (а;0), а ось Оу – в точке М 2 (0;b). Уравнение примет вид:
т.е.
. Это уравнение называетсяуравнением прямой в отрезках, т.к. числа а и b указывают, какие отрезки отсекает прямая на осях координат .

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Найдем уравнение прямой, проходящей через заданную точку Мо (х О; у о) перпендикулярно данному ненулевому вектор n = (А; В).

Возьмем на прямой произвольную точку М(х; у) и рассмотрим вектор М 0 М (х - х 0 ; у - у о) (см. рис.1). Поскольку векторы n и М о М перпендикулярны, то их скалярное произведение равно нулю: то есть

А(х - хо) + В(у - уо) = 0. (10.8)

Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору .

Вектор n= (А; В), перпендикулярный прямой, называется нормальным нормальным вектором этой прямой .

Уравнение (10.8) можно переписать в виде Ах + Ву + С =0 , (10.9)

где А и В координаты нормального вектора, С = -Ах о - Ву о - свободный член. Уравнение (10.9) есть общее уравнение прямой (см. рис.2).

Рис.1 Рис.2

Канонические уравнения прямой

,

Где
- координаты точки, через которую проходит прямая, а
- направляющий вектор.

Кривые второго порядка Окружность

Окружностью называется множество всех точек плоскости, равноотстоящих от данной точки, которая называется центром.

Каноническое уравнение круга радиуса R с центром в точке
:

В частности, если центр кола совпадает с началом координат, то уравнение будет иметь вид:

Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек и, которые называются фокусами, есть величина постоянная
, большая чем расстояние между фокусами
.

Каноническое уравнение эллипса, фокусы которого лежат на оси Ох, а начало координат посредине между фокусами имеет вид
где a длина большой полуоси; b– длина малой полуоси (рис. 2).

Уравнение прямой, проходящей через т.у А(ха; уа) и имеющей угловой коэффициент k, записывается в виде

у – уа=k (x – xa). (5)

Уравнение прямой, проходящей через две точки т. А (х 1 ; у 1) и т.В (х 2 ; у 2) , имеет вид

Если точки А и В определяют прямую, параллельную оси Ох (у 1 = у 2) или оси Оу (х 1 = х 2), то уравнение такой прямой записывается соответственно в виде:

у = у 1 или х = х 1 (7)

Нормальное уравнение прямой

Пусть дана прямая С, проходящая через данную точку Мо(Хо; Уо) и перпендикулярная вектору (А;В). Любой вектор , перпендикулярный данной прямой , называется ее нормальным вектором. Выберем на прямой произвольную т. М(х;у). Тогда , а значит их скалярное произведение . Это равенство можно записать в координатах

А(х-х о)+В(у-у о)=0 (8)

Уравнение (8) называется нормальным уравнением прямой .

Параметрическое и каноническое уравнения прямой

Пусть прямая l задана начальной точкой М 0 (х 0 ; у 0) и направляющим вектором (а 1 ;а 2 ),. Пусть т. М(х; у) – любая точка, лежащая на прямой l . Тогда вектор коллинеарен вектору . Следовательно, = . Записывая это уравнение в координатах, получаем параметрическое уравнение прямой

Исключим параметр t из уравнения (9). Это возможно, так как вектор , и потому хотя бы одна из его координат отлична от нуля.

Пусть и , тогда , и, следовательно,

Уравнение (10) называется каноническим уравнением прямой с направляющим вектором

=(а 1 ; а 2). Если а 1 =0 и , то уравнения (9) примут вид

Этими уравнениями задается прямая, параллельная оси, Оу и проходящая через точку

М 0 (х 0 ; у 0).

х=х 0 (11)

Если , , то уравнения (9) примут вид

Этими уравнениями задается прямая, параллельная оси Ох и проходящая через точку

М 0 (х 0 ; у 0). Каноническое уравнение такой прямой имеет вид

у=у 0 (12)

Угол между прямыми. Условие параллельности и перпендикулярности двух

Прямых

Пусть даны две прямые, заданные общими уравнениями:

и

Тогда угол φ между ними определяется по формуле:

(13)

Условие параллельности 2-х прямых: (14)

Условие перпендикулярности 2-х прямых: (15)

Условие параллельности в этом случае имеет вид: (17)

Условие перпендикулярности прямых: (18)

Если две прямые заданы каноническими уравнениями:

и

то угол φ между этими прямыми определяется по формуле:

(19)

Условие параллельности прямых: (20)

Условие перпендикулярности прямых: (21)

Расстояние от точки до прямой

Расстояние d от точки М(х 1 ; у 1) до прямой Ax+By+C=0 вычисляется по формуле

(22)

Пример по выполнению практической работы

Пример 1. Построить прямую 3х– 2у +6=0.

Решение:Для построения прямой достаточно знать какие-либо две её точки, например, точки её пересечения с осями координат. Точку А пересечения прямой с осью Ох можно получить, если в уравнении прямой принять у=0.Тогда имеем 3х +6=0, т.е. х =-2. Таким образом, А (–2;0).

Тогда В пересечения прямой с осью Оу имеет абсциссу х =0; следовательно, ордината точки В находится из уравнения –2у+ 6=0, т.е. у=3. Таким образом, В (0;3).

Пример 2. Составить уравнение прямой, которая отсекает на отрицательной полуплоскости Оу отрезок, равный 2 единицам, и образует с осью Ох угол φ =30˚.

Решение: Прямая пересекает ось Оу в точке В (0;–2) и имеет угловой коэффициент k =tg φ= = . Полагая в уравнении (2) k = и b = –2, получим искомое уравнение

Или .

Пример 3. А (–1; 2) и

В (0;–3). (указание : угловой коэффициент прямой находится по формуле (3))

Решение: .Отсюда имеем . Подставив в это уравнение координаты т.В, получим: , т.е. начальная ордината b = –3 . Тогда получим уравнение .

Пример 4. Общее уравнение прямой 2х – 3у – 6 = 0 привести к уравнению в отрезках.

Решение: запишем данное уравнение в виде 2х – 3у =6 и разделим обе его части на свободный член: . Это и есть уравнение данной прямой в отрезках.

Пример 5. Через точку А (1;2) провести прямую, отсекающую на положительных полуосях координат равные отрезки.

Решение: Пусть уравнение искомой прямой имеет вид По условию а =b . Следовательно, уравнение принимает вид х + у = а . Так как точка А (1; 2) принадлежит этой прямой, значит ее координаты удовлетворяют уравнению х + у = а ; т.е. 1 + 2 = а , откуда а = 3. Итак, искомое уравнение записывается следующим образом: х + у = 3, или х + у – 3 = 0.

Пример 6. Для прямой написать уравнение в отрезках. Вычислить площадь треугольника, образованного этой прямой и осями координат.

Решение: Преобразуем данное уравнение следующим образом: , или .

В результате получим уравнение , которое и является уравнением данной прямой в отрезках. Треугольник, образованный данной прямой и осями координат, является прямоугольным треугольником с катетами, равными 4 и 3, поэтому его площадь равна S= (кв. ед.)

Пример 7. Составить уравнение прямой, проходящий через точку (–2; 5) и образующей с осью Ох угол 45º.

Решение: Угловой коэффициент искомой прямой k = tg 45º = 1. Поэтому, воспользовавшись уравнением (5), получаем у – 5 = x – (–2), или х – у + 7 = 0.

Пример 8. Составить уравнение прямой, проходящей через точки А (–3; 5)и В(7; –2).

Решение: Воспользуемся уравнением (6):

, или , откуда 7х + 10у – 29 = 0.

Пример 9. Проверить, лежат ли точки А (5; 2), В (3; 1) и С (–1; –1) на одной прямой.

Решение: Составим уравнение прямой, проходящей через точки А и С :

, или

Подставляя в это уравнение координаты точки В (хВ = 3 и у В = 1), получим (3–5) / (–6)= = (1–2) / (–3), т.е. получаем верное равенство. Т. о., координаты точки В удовлетворяют уравнению прямой (АС ), т.е. .

Пример 10: Составить уравнение прямой, проходящую через т. А(2;-3).

Перпендикулярную =(-1;5)

Решение: Пользуясь формулой (8), находим уравнение данной прямой -1(х-2)+5(у+3)=0,

или окончательно, х – 5 у - 17=0.

Пример 11 : Даны точки М 1 (2;-1) и М 2 (4; 5). Написать уравнение прямой, проходящей через точку М 1 перпендикулярно вектору Решение: Нормальный вектор искомой прямой имеет координаты (2;6), следовательно по формуле (8) получим уравнение 2(х-2)+6(у+1)=0 или х+3у +1=0.

Пример 12 : и .

Решение: ; .

Пример 13:

Решение: а) ;

Пример 14: Вычислить угол между прямыми

Решение:

Пример 15: Выяснить взаимное расположение прямых:

Решение:

Пример 16: найти угол между прямыми и .

Решение: .

Пример 17: выяснить взаимное расположение прямых:

Решение:а) - прямые параллельны;

б) - значит, прямые перпендикулярны.

Пример 18: Вычислить расстояние от точки М(6; 8) до прямой

Решение: по формуле (22) получим: .

Задания для практического занятия:

Вариант 1

1. Привести общее уравнение прямой 2x+3y-6=0 к уравнению в отрезках и вычислить площадь треугольника, отсекаемого этой прямой от соответствующего координатного угла;

2. В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);

3. Вычислить угловой коэффициент прямой, проходящей через точку М 0 (-2;4) и параллельной вектору (6;-1);

4. Вычислить угол между прямыми

4. Вычислить угол между прямыми:

а) 2x - 3y + 7 = 0 и 3x - y + 5 = 0 ; б) и y = 2x – 4;

5.Определить взаимное расположение 2-х прямых и ;

, если известны координаты концов отрезка т.А(18;8) и т.В(-2; -6).

Вариант 3

1. Привести общее уравнение прямой 4x-5y+20=0 к уравнению в отрезках и вычислить площадь треугольника, отсекаемого этой прямой от соответствующего координатного угла;

2. В ∆ABC вершины имеют координаты точки А (3;-2), точки В (7;3), точки

С (0;8). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);

3. Вычислить угловой коэффициент прямой, проходящей через точку M 0 (-1;-2) и

параллельной вектору (3;-5);

4. Вычислить угол между прямыми

а) 3x + y - 7 = 0 и x - y + 4 = 0; б) и ;

5. Определить взаимное расположение 2-х прямых и y = 5x + 3;

6. Вычислить расстояние от середины отрезка АВ до прямой , если известны координаты концов отрезка т.А(4;-3) и т.В(-6; 5).

Вариант 4

1. Привести общее уравнение прямой 12x-5y+60=0 к уравнению в отрезках и вычислить длину отрезка, который отсекается от этой прямой соответствующим координатным углом;

2. В ∆ABC вершины имеют координаты точки А (0;-2), точки В (3;6), точки С (1;-4). Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ);

3. Вычислить угловой коэффициент прямой, проходящей через точку M 0 (4;4) и параллельной вектору (-2;7);

4.Вычислить угол между прямыми

а) x +4 y + 8 = 0 и 7x - 3y + 5 = 0; б) и ;

5. Определить взаимное расположение 2-х прямых и ;

6. Вычислить расстояние от середины отрезка АВ до прямой , если известны координаты концов отрезка т.А(-4; 8) и т.В(0; 4).

Контрольные вопросы

1. Назовите уравнения прямой на плоскости, когда известны точка, через которую она проходит и ее направляющий вектор;

2. Какой вид имеет нормальное, общее уравнения прямой на плоскости;

3. Назовите уравнение прямой, проходящей через две точки, уравнение прямой в отрезках, уравнение прямой с угловым коэффициентом;

4. Перечислите формулы для вычисления угла между прямыми, заданными уравнениями с угловым коэффициентом. Сформулируйте условия параллельности и перпендикулярности двух прямых.

5. Как найти расстояние от точки до прямой?

Пусть даны две точки М (Х 1 ,У 1) и N (Х 2, y 2). Найдем уравнение прямой, проходящей через эти точки.

Так как эта прямая проходит через точку М , то согласно формуле (1.13) ее уравнение имеет вид

У – Y 1 = K (X – x 1),

Где K – неизвестный угловой коэффициент.

Значение этого коэффициента определим из того условия, что искомая прямая проходит через точку N , а значит, ее координаты удовлетворяют уравнению (1.13)

Y 2 – Y 1 = K (X 2 – X 1),

Отсюда можно найти угловой коэффициент этой прямой:

,

Или после преобразования

(1.14)

Формула (1.14) определяет Уравнение прямой, проходящей через две точки М (X 1, Y 1) и N (X 2, Y 2).

В частном случае, когда точки M (A , 0), N (0, B ), А ¹ 0, B ¹ 0, лежат на осях координат, уравнение (1.14) примет более простой вид

Уравнение (1.15) называется Уравнением прямой в отрезках , здесь А и B обозначают отрезки, отсекаемые прямой на осях (рисунок 1.6).

Рисунок 1.6

Пример 1.10. Составить уравнение прямой, проходящей через точки М (1, 2) и B (3, –1).

. Согласно (1.14) уравнение искомой прямой имеет вид

2(Y – 2) = -3(X – 1).

Перенося все члены в левую часть, окончательно получаем искомое уравнение

3X + 2Y – 7 = 0.

Пример 1.11. Составить уравнение прямой, проходящей через точку М (2, 1) и точку пересечения прямых X + Y – 1 = 0, Х – у + 2 = 0.

. Координаты точки пересечения прямых найдем, решив совместно данные уравнения

Если сложить почленно эти уравнения, получим 2X + 1 = 0, откуда . Подставив найденное значение в любое уравнение, найдем значение ординаты У :

Теперь напишем уравнение прямой, проходящей через точки (2, 1) и :

или .

Отсюда или –5(Y – 1) = X – 2.

Окончательно получаем уравнение искомой прямой в виде Х + 5Y – 7 = 0.

Пример 1.12. Найти уравнение прямой, проходящей через точки M (2,1) и N (2,3).

Используя формулу (1.14), получим уравнение

Оно не имеет смысла, так как второй знаменатель равен нулю. Из условия задачи видно, что абсциссы обеих точек имеют одно и то же значение. Значит, искомая прямая параллельна оси ОY и ее уравнение имеет вид: x = 2.

Замечание . Если при записи уравнения прямой по формуле (1.14) один из знаменателей окажется равным нулю, то искомое уравнение можно получить, приравняв к нулю соответствующий числитель.

Рассмотрим другие способы задания прямой на плоскости.

1. Пусть ненулевой вектор перпендикулярен данной прямой L , а точка M 0(X 0, Y 0) лежит на этой прямой (рисунок 1.7).

Рисунок 1.7

Обозначим М (X , Y ) произвольную точку на прямой L . Векторы и Ортогональны. Используя условия ортогональности этих векторов, получим или А (X – X 0) + B (Y – Y 0) = 0.

Мы получили уравнение прямой, проходящей через точку M 0 перпендикулярно вектору . Этот вектор называется Вектором нормали к прямой L . Полученное уравнение можно переписать в виде

Ах + Ву + С = 0, где С = –(А X 0 + By 0), (1.16),

Где А и В – координаты вектора нормали.

Получим общее уравнение прямой в параметрическом виде.

2. Прямую на плоскости можно задать так: пусть ненулевой вектор параллелен данной прямой L и точка M 0(X 0, Y 0) лежит на этой прямой. Вновь возьмем произвольную точку М (Х , y) на прямой (рисунок 1.8).

Рисунок 1.8

Векторы и коллинеарны.

Запишем условие коллинеарности этих векторов: , где T – произвольное число, называемое параметром. Распишем это равенство в координатах:

Эти уравнения называются Параметрическими уравнениями Прямой . Исключим из этих уравнений параметр T :

Эти уравнения иначе можно записать в виде

. (1.18)

Полученное уравнение называют Каноническим уравнением прямой . Вектор называют Направляющим вектором прямой .

Замечание . Легко видеть, что если – вектор нормали к прямой L , то ее направляющим вектором может быть вектор , так как , т. е. .

Пример 1.13. Написать уравнение прямой, проходящей через точку M 0(1, 1) параллельно прямой 3Х + 2У – 8 = 0.

Решение . Вектор является вектором нормали к заданной и искомой прямым. Воспользуемся уравнением прямой, проходящей через точку M 0 с заданным вектором нормали 3(Х –1) + 2(У – 1) = 0 или 3Х + 2у – 5 = 0. Получили уравнение искомой прямой.

Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Определение точки пересечения двух прямых

1. Уравнение прямой, проходящей через данную точку A (x 1 , y 1) в данном направлении, определяемом угловым коэффициентом k ,

y - y 1 = k (x - x 1). (1)

Это уравнение определяет пучок прямых, проходящих через точку A (x 1 , y 1), которая называется центром пучка.

2. Уравнение прямой, проходящей через две точки: A (x 1 , y 1) и B (x 2 , y 2), записывается так:

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B . Если две прямые заданы уравнениями с угловым коэффициентом

y = k 1 x + B 1 ,