Osnovne elementarne funkcije i njihova svojstva. Osnovna svojstva funkcija

Kompletan popis osnovnih elementarnih funkcija

Klasa osnovnih elementarnih funkcija uključuje sljedeće:

Konstantna funkcija $y=C$, gdje je $C$ konstanta. Takva funkcija uzima istu vrijednost $C$ za bilo koji $x$.
Funkcija stepena $y=x^(a) $, gdje je eksponent $a$ realan broj.
Eksponencijalna funkcija $y=a^(x) $, gdje je baza stupanj $a>0$, $a\ne 1$.
Logaritamska funkcija $y=\log _(a) x$, gdje je baza logaritma $a>0$, $a\ne 1$.
Trigonometrijske funkcije $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ sek\,x$.
Inverzne trigonometrijske funkcije $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , x$.

Funkcije snage

Razmotrit ćemo ponašanje funkcije potencije $y=x^(a) $ za one najjednostavnije slučajeve kada njezin eksponent određuje cjelobrojno potenciranje i vađenje korijena.

Slučaj 1

Eksponent funkcije $y=x^(a) $ je prirodan broj, odnosno $y=x^(n) $, $n\in N$.

Ako je $n=2\cdot k$ paran broj, tada je funkcija $y=x^(2\cdot k) $ paran i neograničeno raste kao da argument $\left(x\to +\infty \ right )$, a s njegovim neograničenim smanjenjem $\left(x\to -\infty \right)$. Ovo ponašanje funkcije može se opisati izrazima $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ i $\mathop(\lim )\ limits_(x\to -\infty ) x^(2\cdot k) =+\infty $, što znači da funkcija u oba slučaja raste bez ograničenja ($\lim $ je granica). Primjer: graf funkcije $y=x^(2) $.

Ako je $n=2\cdot k-1$ neparan broj, tada je funkcija $y=x^(2\cdot k-1) $ neparna, neograničeno raste kako argument raste neograničeno, a opada neograničeno kako argument smanjuje unedogled. Ovo ponašanje funkcije može se opisati izrazima $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ i $\mathop(\lim )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. Primjer: graf funkcije $y=x^(3) $.

Slučaj 2

Eksponent funkcije $y=x^(a) $ je negativan cijeli broj, to jest $y=\frac(1)(x^(n) ) $, $n\in N$.

Ako je $n=2\cdot k$ paran broj, tada je funkcija $y=\frac(1)(x^(2\cdot k) ) $ paran i asimptotski (postupno) se približava nuli kao s argumentom neograničenog povećanja , te s njegovim neograničenim smanjenjem. Ovo ponašanje funkcije može se opisati jednim izrazom $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$, što znači da s neograničenim porastom argumenta u apsolutnoj vrijednosti limit funkcije je nula. Nadalje, kako argument teži nuli i lijevo $\lijevo(x\to 0-0\desno)$ i desno $\lijevo(x\to 0+0\desno)$, funkcija raste bez ograničiti. Prema tome, izrazi $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ i $\mathop(\lim )\ granice_ su važeće (x\to 0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, što znači da je funkcija $y=\frac(1)(x^(2 \cdot k ) ) $ u oba slučaja ima beskonačnu granicu jednaku $+\infty $. Primjer: graf funkcije $y=\frac(1)(x^(2) ) $.

Ako je $n=2\cdot k-1$ neparan broj, tada je funkcija $y=\frac(1)(x^(2\cdot k-1) ) $ neparna i asimptotski se približava nuli kao da oboje kada argument se povećava i kada se neograničeno smanjuje. Ovo ponašanje funkcije može se opisati jednim izrazom $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$. Osim toga, kako se argument približava nuli s lijeve strane, funkcija opada bez ograničenja, a kako se argument približava nuli s desne strane, funkcija raste bez ograničenja, to jest, $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ i $\mathop(\lim )\limits_(x\to 0+0) \frac(1)( x^(2\cdot k-1) ) =+\infty $. Primjer: graf funkcije $y=\frac(1)(x) $.

Slučaj 3

Eksponent funkcije $y=x^(a) $ je inverz prirodnog broja, to jest, $y=\sqrt[(n)](x) $, $n\in N$.

Ako je $n=2\cdot k$ paran broj, tada je funkcija $y=\pm \sqrt[(2\cdot k)](x) $ dvovrijedna i definirana je samo za $x\ge 0 $. Neograničenim povećanjem argumenta vrijednost funkcije $y=+\sqrt[(2\cdot k)](x) $ neograničeno raste, a vrijednost funkcije $y=-\sqrt[(2\ cdot k)](x) $ neograničeno opada, to jest $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right )=+\infty $ i $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. Primjer: graf funkcije $y=\pm \sqrt(x) $.

Ako je $n=2\cdot k-1$ neparan broj, tada je funkcija $y=\sqrt[(2\cdot k-1)](x) $ neparna, raste neograničeno s neograničenim povećanjem argumenta i neograničeno se smanjuje kada je neograničeno, smanjuje se, to jest, $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ i $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. Primjer: graf funkcije $y=\sqrt[(3)](x) $.

Eksponencijalne i logaritamske funkcije

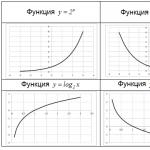
Eksponencijalna $y=a^(x) $ i logaritamska $y=\log _(a) x$ funkcija međusobno su inverzne. Njihovi su grafikoni simetrični u odnosu na zajedničku simetralu prvog i trećeg koordinatnog kuta.

Kada se argument $\left(x\to +\infty \right)$ neograničeno povećava, eksponencijalna funkcija ili $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ raste neograničeno, ako je $a>1$, ili se asimptotski približava nuli $\mathop(\lim)\limits_(x\to +\infty) a^(x) =0$, ako je $a1$, ili $\mathop raste bez ograničenja (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, ako $a

Karakteristična vrijednost za funkciju $y=a^(x) $ je vrijednost $x=0$. U tom slučaju sve eksponencijalne funkcije, bez obzira na $a$, nužno sijeku $Oy$ os u $y=1$. Primjeri: grafovi funkcija $y=2^(x) $ i $y = \lijevo (\frac(1)(2) \desno)^(x) $.

Logaritamska funkcija $y=\log _(a) x$ definirana je samo za $x > 0$.

Kako argument $\left(x\to +\infty \right)$ raste neograničeno, logaritamska funkcija ili $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+ \ povećava neograničeno infty $, ako $a>1$, ili se smanjuje bez ograničenja $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, ako $a1 $, ili bez ograničenja $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $ raste ako $a

Karakteristična vrijednost za funkciju $y=\log _(a) x$ je vrijednost $y=0$. U tom slučaju sve logaritamske funkcije, bez obzira na $a$, nužno sijeku $Ox$ os u $x=1$. Primjeri: grafovi funkcija $y=\log _(2) x$ i $y=\log _(1/2) x$.

Neke logaritamske funkcije imaju posebne oznake. Konkretno, ako je baza logaritma $a=10$, tada se takav logaritam naziva decimalnim, a odgovarajuća funkcija se piše kao $y=\lg x$. A ako se kao baza logaritma odabere iracionalni broj $e=2,7182818\ldots $, tada se takav logaritam naziva prirodnim, a odgovarajuća funkcija se piše kao $y=\ln x$. Njen inverz je funkcija $y=e^(x) $, koja se naziva eksponent.

Osnovne elementarne funkcije su: stalna funkcija (konstanta), korijen n- stupanj, potencija, eksponencijalna, logaritamska funkcija, trigonometrijska i inverzna trigonometrijska funkcija.

Stalna funkcija.

Konstantna funkcija dana je na skupu svih realnih brojeva formulom , gdje je C– neki realni broj. Konstantna funkcija dodjeljuje svaku stvarnu vrijednost nezavisne varijable x ista vrijednost zavisne varijable g- značenje S. Konstantna funkcija naziva se i konstanta.

Graf konstantne funkcije je ravna linija paralelna s x-osi koja prolazi točkom s koordinatama (0,C). Na primjer, pokažimo grafove konstantnih funkcija y=5,y=-2 i , koji na donjoj slici odgovaraju crnim, crvenim i plavim linijama.

Svojstva konstantne funkcije.

Domena: cijeli skup realnih brojeva.

Konstantna funkcija je parna.

Raspon vrijednosti: skup koji se sastoji od jednog broja S.

Konstantna funkcija je nerastuća i neopadajuća (zato je i konstantna).

O konveksnosti i konkavnosti konstante nema smisla govoriti.

Nema asimptota.

Funkcija prolazi kroz točku (0,C) koordinatna ravnina.

Korijen n-tog stupnja.

Razmotrimo osnovnu elementarnu funkciju, koja je dana formulom, gdje je n– prirodni broj veći od jedan.

N-ti korijen, n je paran broj.

Počnimo s root funkcijom n-tu potenciju za parne vrijednosti eksponenta korijena n.

Kao primjer, ovdje je slika sa slikama grafova funkcija i odgovaraju crnim, crvenim i plavim linijama.

Grafikoni korijenskih funkcija parnog stupnja imaju sličan izgled za druge vrijednosti eksponenta.

Svojstva korijenske funkcijen -ta snaga za parn .

N-ti korijen, n je neparan broj.

Funkcija korijena n-tu potenciju s eksponentom neparnog korijena n je definiran na cijelom skupu realnih brojeva. Na primjer, ovdje su grafikoni funkcija i odgovaraju crnim, crvenim i plavim krivuljama.

1) Domena funkcije i područje funkcije.

Domena funkcije je skup svih valjanih valjanih vrijednosti argumenata x(varijabilno x), za koju je funkcija y = f(x) odlučan. Raspon funkcije je skup svih realnih vrijednosti g, što funkcija prihvaća.

U elementarnoj matematici funkcije se proučavaju samo na skupu realnih brojeva.

2) Funkcijske nule.

Funkcija nula je vrijednost argumenta pri kojoj je vrijednost funkcije jednaka nuli.

3) Intervali konstantnog predznaka funkcije.

Intervali konstantnog predznaka funkcije su skupovi vrijednosti argumenata na kojima su vrijednosti funkcije samo pozitivne ili samo negativne.

4) Monotonost funkcije.

Rastuća funkcija (u određenom intervalu) je funkcija kod koje većoj vrijednosti argumenta iz tog intervala odgovara veća vrijednost funkcije.

Opadajuća funkcija (u određenom intervalu) je funkcija kod koje manja vrijednost funkcije odgovara većoj vrijednosti argumenta iz tog intervala.

5) Parna (neparna) funkcija.

Parna funkcija je funkcija čija je definicijska domena simetrična s obzirom na ishodište i za bilo koji x iz domene definicije jednakost f(-x) = f(x). Graf parne funkcije je simetričan u odnosu na ordinatu.

Neparna funkcija je funkcija čija je definicijska domena simetrična s obzirom na ishodište i za bilo koji x iz domene definicije jednakost je istinita f(-x) = - f(x). Graf neparne funkcije je simetričan oko ishodišta.

6) Ograničene i neograničene funkcije.

Funkcija se naziva ograničenom ako postoji pozitivan broj M takav da je |f(x)| ≤ M za sve vrijednosti x. Ako takav broj ne postoji, funkcija je neograničena.

7) Periodičnost funkcije.

Funkcija f(x) je periodična ako postoji broj T različit od nule da za bilo koji x iz domene definicije funkcije vrijedi: f(x+T) = f(x). Taj najmanji broj naziva se periodom funkcije. Sve trigonometrijske funkcije su periodične. (Trigonometrijske formule).

19. Osnovne elementarne funkcije, njihova svojstva i grafovi. Primjena funkcija u ekonomiji.

Osnovne elementarne funkcije. Njihova svojstva i grafikoni

1. Linearna funkcija.

Linearna funkcija naziva se funkcija oblika , gdje je x varijabla, a i b realni brojevi.

Broj A koji se naziva nagib pravca, jednak je tangensu kuta nagiba ovog pravca na pozitivan smjer osi apscise. Graf linearne funkcije je pravac. Definiraju ga dvije točke.

Svojstva linearne funkcije

1. Domena definicije - skup svih realnih brojeva: D(y)=R

2. Skup vrijednosti je skup svih realnih brojeva: E(y)=R

3. Funkcija poprima nultu vrijednost kada ili.

4. Funkcija raste (opada) u cijeloj domeni definicije.

5. Linearna funkcija je kontinuirana na cijelom području definicije, diferencijabilna i .

2. Kvadratna funkcija.

Funkcija oblika gdje je x varijabla, koeficijenti a, b, c realni brojevi naziva se kvadratni

Promatrajući funkcije kompleksne varijable, Liouville je elementarne funkcije definirao nešto šire. Elementarna funkcija g varijabla x- analitička funkcija, koja se može prikazati kao algebarska funkcija x i funkcije , i logaritam je ili eksponent neke algebarske funkcije g 1 od x .

Na primjer, grijeh( x) - algebarska funkcija od e jax .

Bez ograničavanja općenitosti razmatranja, možemo smatrati da su funkcije algebarski neovisne, to jest ako je algebarska jednadžba zadovoljena za sve x, zatim svi koeficijenti polinoma jednaki su nuli.

Diferencijacija elementarnih funkcija

Gdje z 1 "(z) jednako ili g 1 " / g 1 ili z 1 g 1" ovisno o tome radi li se o logaritmu z 1 ili eksponencijalni itd. U praksi je zgodno koristiti tablicu izvoda.

Integriranje elementarnih funkcija

Liouvilleov teorem je osnova za stvaranje algoritama za simboličku integraciju elementarnih funkcija, implementiranih npr.

Izračun granica

Liouvilleova teorija ne odnosi se na izračun granica. Ne zna se postoji li algoritam koji za niz zadan elementarnom formulom daje odgovor ima li limit ili ne. Na primjer, otvoreno je pitanje da li niz konvergira.

Književnost

J. Liouville. Mémoire sur l'intégration d'une classe de fonctions transcendantes// J. Reine Angew. matematika Bd. 13, str. 93-118 (prikaz, ostalo). (1835)
J.F. Ritt. Integracija u konačnim terminima. N.-Y., 1949 // http://lib.homelinux.org
A. G. Khovanski. Topološka Galoisova teorija: rješivost i nerješivost jednadžbi u konačnom obliku CH. 1. M, 2007. (monografija).

Bilješke

Zaklada Wikimedia. 2010.

Elementarna ekscitacija
Elementarni ishod

Pogledajte što je "elementarna funkcija" u drugim rječnicima:

elementarna funkcija- Funkcija koja se, ako se podijeli na manje funkcije, ne može jednoznačno definirati u hijerarhiji digitalnog prijenosa. Stoga je sa stajališta mreže nedjeljiv (ITU T G.806). Teme: telekomunikacije, osnovni pojmovi EN funkcija prilagodbeA... Vodič za tehničke prevoditelje

funkcija interakcije između mrežnih razina- Elementarna funkcija koja osigurava interakciju karakterističnih informacija između dva mrežna sloja. (ITU T G.806). Teme: telekomunikacije, osnovni koncepti EN sloja... ... Vodič za tehničke prevoditelje