Funcții elementare de bază și proprietățile lor. Proprietățile de bază ale funcțiilor

Lista completă a funcțiilor elementare de bază

Clasa de funcții elementare de bază include următoarele:

1. Funcția constantă $y=C$, unde $C$ este o constantă. O astfel de funcție ia aceeași valoare $C$ pentru orice $x$.
2. Funcția de putere $y=x^(a) $, unde exponentul $a$ este un număr real.
3. Funcția exponențială $y=a^(x) $, unde baza este gradul $a>0$, $a\ne 1$.
4. Funcția logaritmică $y=\log _(a) x$, unde baza logaritmului este $a>0$, $a\ne 1$.
5. Funcții trigonometrice $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ sec\,x$.
6. Funcții trigonometrice inverse $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , x$.

Funcții de putere

Vom lua în considerare comportamentul funcției de putere $y=x^(a) $ pentru acele mai simple cazuri când exponentul său determină exponențiarea întregului și extragerea rădăcinilor.

Cazul 1

Exponentul funcției $y=x^(a) $ este un număr natural, adică $y=x^(n) $, $n\în N$.

Dacă $n=2\cdot k$ este un număr par, atunci funcția $y=x^(2\cdot k) $ este par și crește la infinit ca și cum argumentul $\left(x\to +\infty \ right )$ și cu scăderea sa nelimitată $\left(x\to -\infty \right)$. Acest comportament al funcției poate fi descris prin expresiile $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ și $\mathop(\lim )\ limits_(x\to -\infty ) x^(2\cdot k) =+\infty $, ceea ce înseamnă că funcția în ambele cazuri crește fără limită ($\lim $ este limita). Exemplu: graficul funcției $y=x^(2) $.

Dacă $n=2\cdot k-1$ este un număr impar, atunci funcția $y=x^(2\cdot k-1) $ este impară, crește la infinit pe măsură ce argumentul crește la nesfârșit și scade la infinit ca argument scade la infinit. Acest comportament al funcției poate fi descris prin expresiile $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ și $\mathop(\lim )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. Exemplu: graficul funcției $y=x^(3) $.

Cazul 2

Exponentul funcției $y=x^(a) $ este un întreg negativ, adică $y=\frac(1)(x^(n) ) $, $n\în N$.

Dacă $n=2\cdot k$ este un număr par, atunci funcția $y=\frac(1)(x^(2\cdot k) ) $ este par și asimptotic (treptat) se apropie de zero ca și cu argumentul de creștere nelimitată , și cu scăderea sa nelimitată. Acest comportament al funcției poate fi descris printr-o singură expresie $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$, ceea ce înseamnă că cu o creștere nelimitată a argumentului în valoare absolută, limita funcției este zero. În plus, deoarece argumentul tinde spre zero atât în ​​stânga $\left(x\to 0-0\right)$ cât și în dreapta $\left(x\to 0+0\right)$, funcția crește fără limită. Prin urmare, expresiile $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ și $\mathop(\lim )\ limitele_ sunt valide (x\to 0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, ceea ce înseamnă că funcția $y=\frac(1)(x^(2) \cdot k ) ) $ în ambele cazuri are o limită infinită egală cu $+\infty $. Exemplu: graficul funcției $y=\frac(1)(x^(2) ) $.

Dacă $n=2\cdot k-1$ este un număr impar, atunci funcția $y=\frac(1)(x^(2\cdot k-1) ) $ este impar și se apropie asimptotic de zero, ca și cum ambele atunci când argumentul crește și când scade fără limită. Acest comportament al funcției poate fi descris printr-o singură expresie $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$. În plus, pe măsură ce argumentul se apropie de zero în stânga, funcția scade fără limită, iar pe măsură ce argumentul se apropie de zero în dreapta, funcția crește fără limită, adică $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ și $\mathop(\lim )\limits_(x\to 0+0) \frac(1)( x^(2\cdot k-1) ) =+\infty $. Exemplu: graficul funcției $y=\frac(1)(x) $.

Cazul 3

Exponentul funcției $y=x^(a) $ este inversul numărului natural, adică $y=\sqrt[(n)](x) $, $n\în N$.

Dacă $n=2\cdot k$ este un număr par, atunci funcția $y=\pm \sqrt[(2\cdot k)](x) $ are două valori și este definită numai pentru $x\ge 0 $. Cu o creștere nelimitată a argumentului, valoarea funcției $y=+\sqrt[(2\cdot k)](x) $ crește nelimitat, iar valoarea funcției $y=-\sqrt[(2\ cdot k)](x) $ scade nelimitat, adică $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right )=+\infty $ și $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. Exemplu: graficul funcției $y=\pm \sqrt(x) $.

Dacă $n=2\cdot k-1$ este un număr impar, atunci funcția $y=\sqrt[(2\cdot k-1)](x) $ este impar, crește nelimitat cu o creștere nelimitată a argumentului și scade nelimitat atunci când este nelimitat, scade, adică $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ și $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. Exemplu: graficul funcției $y=\sqrt[(3)](x) $.

Funcții exponențiale și logaritmice

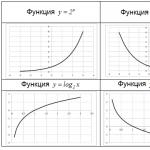
Funcțiile exponențiale $y=a^(x) $ și logaritmice $y=\log _(a) x$ sunt reciproc inverse. Graficele lor sunt simetrice față de bisectoarea comună a primului și a treilea unghi de coordonate.

Când argumentul $\left(x\to +\infty \right)$ crește la nesfârșit, funcția exponențială sau $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ crește la nesfârșit, dacă $a>1$, sau se apropie asimptotic de zero $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =0$, dacă $a1$ sau $\mathop crește fără limită (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, dacă $a

Valoarea caracteristică pentru funcția $y=a^(x) $ este valoarea $x=0$. În acest caz, toate funcțiile exponențiale, indiferent de $a$, intersectează în mod necesar axa $Oy$ la $y=1$. Exemple: grafice ale funcțiilor $y=2^(x) $ și $y = \left (\frac(1)(2) \right)^(x) $.

Funcția logaritmică $y=\log _(a) x$ este definită numai pentru $x > 0$.

Pe măsură ce argumentul $\left(x\to +\infty \right)$ crește la nesfârșit, funcția logaritmică sau $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+ \ crește la infinit la infinit $, dacă $a>1$, sau scade fără limită $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, dacă $a1 $, sau fără limită $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $ crește dacă $a

Valoarea caracteristică pentru funcția $y=\log _(a) x$ este valoarea $y=0$. În acest caz, toate funcțiile logaritmice, indiferent de $a$, intersectează în mod necesar axa $Ox$ la $x=1$. Exemple: grafice ale funcțiilor $y=\log _(2) x$ și $y=\log _(1/2) x$.

Unele funcții logaritmice au notație specială. În special, dacă baza logaritmului este $a=10$, atunci un astfel de logaritm se numește zecimal, iar funcția corespunzătoare este scrisă ca $y=\lg x$. Și dacă numărul irațional $e=2.7182818\ldots $ este ales ca bază a logaritmului, atunci un astfel de logaritm se numește natural, iar funcția corespunzătoare este scrisă ca $y=\ln x$. Inversa sa este funcția $y=e^(x) $, numită exponent.

Funcții elementare de bază sunt: ​​funcție constantă (constant), rădăcină n-gradul, funcția de putere, funcția exponențială, logaritmică, funcțiile trigonometrice și trigonometrice inverse.

Funcție permanentă.

O funcție constantă este dată pe mulțimea tuturor numerelor reale prin formula , unde C– un număr real. O funcție constantă atribuie fiecare valoare reală a variabilei independente X aceeași valoare a variabilei dependente y- sens CU. O funcție constantă se mai numește și constantă.

Graficul unei funcții constante este o dreaptă paralelă cu axa x și care trece prin punctul cu coordonate (0,C). De exemplu, să arătăm grafice ale funcțiilor constante y=5,y=-2și , care în figura de mai jos corespund liniilor negre, roșii și, respectiv, albastre.

Proprietățile unei funcții constante.

Domeniu: întregul set de numere reale.

Funcția constantă este pară.

Interval de valori: set format dintr-un număr singular CU.

O funcție constantă nu crește și nu descrește (de aceea este constantă).

Nu are sens să vorbim despre convexitatea și concavitatea unei constante.

Nu există asimptote.

Funcția trece prin punct (0,C) plan de coordonate.

Rădăcina gradului al n-lea.

Să luăm în considerare funcția elementară de bază, care este dată de formula, unde n– un număr natural mai mare decât unu.

Rădăcina a n-a, n este un număr par.

Să începem cu funcția rădăcină n-a puterea pentru valorile pare ale exponentului rădăcină n.

Ca exemplu, iată o imagine cu imagini ale graficelor de funcții și , acestea corespund liniilor negre, roșii și albastre.

Graficele funcțiilor rădăcinii de grad par au un aspect similar pentru alte valori ale exponentului.

Proprietățile funcției rădăcinăn -a putere pentru parn .

Rădăcina a n-a, n este un număr impar.

Funcția rădăcină n-a putere cu un exponent rădăcină impar n este definită pe întregul set de numere reale. De exemplu, aici sunt graficele funcțiilor și , acestea corespund curbelor negre, roșii și albastre.

1) Domeniul funcției și domeniul de funcții.

Domeniul unei funcții este setul tuturor valorilor argumentelor valide X(variabil X), pentru care funcția y = f(x) determinat. Domeniul unei funcții este mulțimea tuturor valorilor reale y, pe care funcția îl acceptă.

În matematica elementară, funcțiile sunt studiate numai pe mulțimea numerelor reale.

2) Zerourile funcției.

Funcția zero este valoarea argumentului la care valoarea funcției este egală cu zero.

3) Intervale de semn constant al unei funcții.

Intervalele de semn constant ale unei funcții sunt seturi de valori ale argumentelor pe care valorile funcției sunt doar pozitive sau numai negative.

4) Monotonitatea funcției.

O funcție crescătoare (într-un anumit interval) este o funcție în care o valoare mai mare a argumentului din acest interval îi corespunde unei valori mai mari a funcției.

O funcție descrescătoare (într-un anumit interval) este o funcție în care o valoare mai mare a argumentului din acest interval îi corespunde unei valori mai mici a funcției.

5) Funcția par (impar)..

O funcție pară este o funcție al cărei domeniu de definiție este simetric față de origine și pentru oricare X din domeniul definirii egalitatea f(-x) = f(x). Graficul unei funcții pare este simetric față de ordonată.

O funcție impară este o funcție al cărei domeniu de definiție este simetric față de origine și pentru oricare X din domeniul definiției egalitatea este adevărată f(-x) = - f(x). Graficul unei funcții impare este simetric față de origine.

6) Funcții limitate și nelimitate.

O funcție se numește mărginită dacă există un număr M pozitiv astfel încât |f(x)| ≤ M pentru toate valorile lui x. Dacă un astfel de număr nu există, atunci funcția este nelimitată.

7) Periodicitatea funcției.

O funcție f(x) este periodică dacă există un număr T diferit de zero, astfel încât pentru orice x din domeniul de definire al funcției se respectă următoarele: f(x+T) = f(x). Acest număr cel mai mic se numește perioada funcției. Toate funcțiile trigonometrice sunt periodice. (Formulele trigonometrice).

19. Funcții elementare de bază, proprietățile și graficele lor. Aplicarea funcțiilor în economie.

Funcții elementare de bază. Proprietățile și graficele lor

1. Funcția liniară.

Funcție liniară se numește funcție de forma , unde x este o variabilă, a și b sunt numere reale.

Număr A numită panta dreptei, este egală cu tangenta unghiului de înclinare a acestei linii la direcția pozitivă a axei x. Graficul unei funcții liniare este o linie dreaptă. Este definit de două puncte.

Proprietățile unei funcții liniare

1. Domeniul definiției - mulțimea tuturor numerelor reale: D(y)=R

2. Mulțimea valorilor este mulțimea tuturor numerelor reale: E(y)=R

3. Funcția ia o valoare zero când sau.

4. Funcția crește (descrește) pe întregul domeniu de definire.

5. O funcție liniară este continuă pe întregul domeniu al definiției, diferențiabilă și .

2. Funcția pătratică.

O funcție de forma, unde x este o variabilă, coeficienții a, b, c sunt numere reale, se numește pătratică.

Luând în considerare funcțiile unei variabile complexe, Liouville a definit funcțiile elementare oarecum mai larg. Funcția elementară y variabil X- funcţie analitică, care poate fi reprezentată ca o funcţie algebrică a X si functii , și este logaritmul sau exponentul unei funcții algebrice g 1 din X .

De exemplu, păcatul( X) - funcţie algebrică a e iX .

Fără a limita generalitatea considerației, putem considera că funcțiile sunt independente din punct de vedere algebric, adică dacă ecuația algebrică este satisfăcută pentru toate X, apoi toți coeficienții polinomului sunt egale cu zero.

Diferențierea funcțiilor elementare

Unde z 1 "(z) egal cu sau g 1 " / g 1 sau z 1 g 1" în funcție de faptul că este un logaritm z 1 sau exponențial etc. În practică, este convenabil să folosiți un tabel derivat.

Integrarea funcţiilor elementare

Teorema lui Liouville stă la baza creării algoritmilor pentru integrarea simbolică a funcțiilor elementare, implementați, de exemplu, în

Calculul limitelor

Teoria lui Liouville nu se aplică la calculul limitelor. Nu se știe dacă există un algoritm care, dată fiind o succesiune dată de o formulă elementară, să dea un răspuns dacă are sau nu limită. De exemplu, întrebarea este deschisă dacă secvența converge.

Literatură

• J. Liouville. Memorie de integrare a unei clase de funcții transcendante// J. Reine Angew. Matematică. Bd. 13, p. 93-118. (1835)
• J.F. Ritt. Integrare în termeni finiți. N.-Y., 1949 // http://lib.homelinux.org
• A. G. Khovansky. Teoria topologică Galois: solvabilitatea și insolubilitatea ecuațiilor în formă finită Ch. 1. M, 2007

Note

Fundația Wikimedia. 2010.

• Excitație elementară
• Rezultat elementar

Vedeți ce este „Funcția elementară” în alte dicționare:

funcţie elementară- O funcție care, dacă este împărțită în funcții mai mici, nu poate fi definită în mod unic în ierarhia transmisiei digitale. Prin urmare, din punctul de vedere al rețelei este indivizibilă (ITU T G.806). Subiecte: telecomunicații, concepte de bază Funcția de adaptare la ENA... Ghidul tehnic al traducătorului

funcţia de interacţiune între nivelurile de reţea- O funcție elementară care asigură interacțiunea informațiilor caracteristice între două straturi de rețea. (ITU T G.806). Subiecte: telecomunicații, concepte de bază ale stratului EN... ... Ghidul tehnic al traducătorului