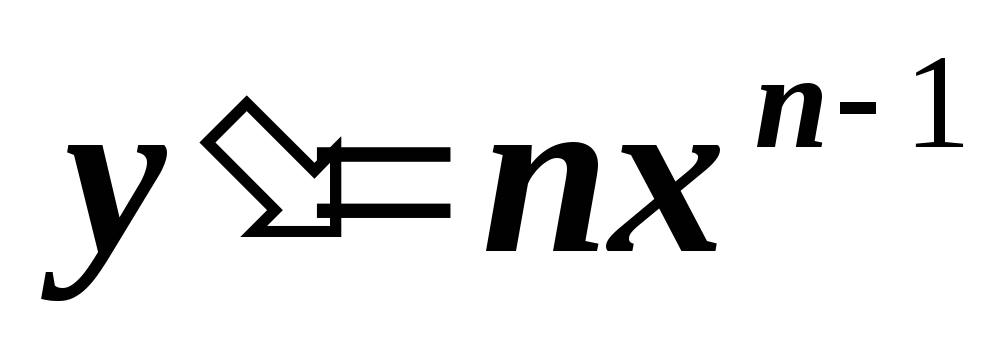Formulas for reducing logarithms. Natural logarithm, ln x function
The logarithm of a number N by reason a is called exponent X , to which you need to raise a to get the number N
Provided that 
,
,
It follows from the definition of the logarithm that 
, i.e.
- this equality is the basic logarithmic identity.
Logarithms to base 10 are called decimal logarithms. Instead of 
write 
.
base logarithms e
are called natural and denoted 
.
Basic properties of logarithms.
The logarithm of unity for any base is zero
The logarithm of the product is equal to the sum of the logarithms of the factors.
3) The logarithm of the quotient is equal to the difference of the logarithms
Factor 
is called the modulus of transition from logarithms at the base a
to logarithms at the base b
.
Using properties 2-5, it is often possible to reduce the logarithm of a complex expression to the result of simple arithmetic operations on logarithms.
For example, 
Such transformations of the logarithm are called logarithms. Transformations reciprocal of logarithms are called potentiation.
Chapter 2. Elements of higher mathematics.
1. Limits
function limit 
is a finite number A if, when striving xx
0
for each predetermined 
, there is a number 
that as soon as 
, then 
.
A function that has a limit differs from it by an infinitesimal amount: 
, where - b.m.w., i.e.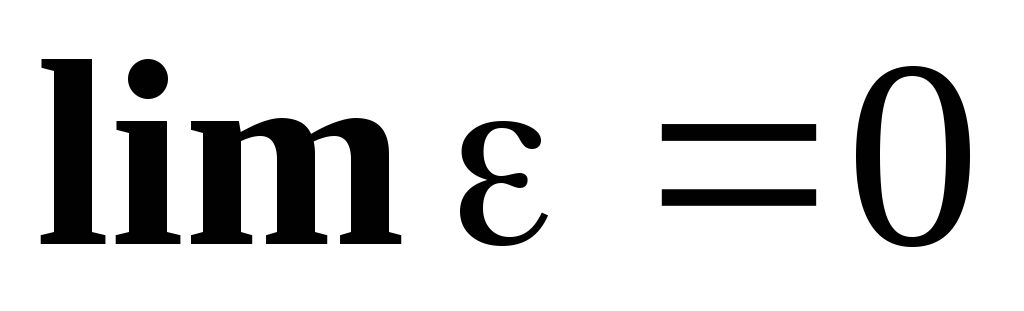 
.
Example. Consider the function 
.
When striving 
, function y
goes to zero: 
1.1. Basic theorems about limits.
The limit of a constant value is equal to this constant value
.
The limit of the sum (difference) of a finite number of functions is equal to the sum (difference) of the limits of these functions.
The limit of a product of a finite number of functions is equal to the product of the limits of these functions.
The limit of the quotient of two functions is equal to the quotient of the limits of these functions if the limit of the denominator is not equal to zero.
Remarkable Limits
,
, where 
1.2. Limit Calculation Examples
However, not all limits are calculated so easily. More often, the calculation of the limit is reduced to the disclosure of type uncertainty: 
or .
.
2. Derivative of a function
Let we have a function 
, continuous on the segment 
.
Argument 
got some boost 
. Then the function will be incremented 
.
Argument value 
corresponds to the value of the function 
.
Argument value 
corresponds to the value of the function .
Hence, .
Let us find the limit of this relation at 
. If this limit exists, then it is called the derivative of the given function.
Definition of the 3derivative of a given function 
by argument 
called the limit of the ratio of the increment of the function to the increment of the argument, when the increment of the argument arbitrarily tends to zero.
Function derivative 
can be denoted as follows:
;
;
;
.
Definition 4The operation of finding the derivative of a function is called differentiation.
2.1. The mechanical meaning of the derivative.
Consider the rectilinear motion of some rigid body or material point.
Let at some point in time 
moving point 
was at a distance 
from the starting position 
.
After some period of time 
she moved a distance 
. Attitude 
=
- average speed of a material point 
. Let us find the limit of this ratio, taking into account that 
.
Consequently, the determination of the instantaneous velocity of a material point is reduced to finding the derivative of the path with respect to time.
2.2. Geometric value of the derivative
Suppose we have a graphically defined some function 
.
Rice. 1. The geometric meaning of the derivative
If a 
, then the point 
, will move along the curve, approaching the point 
.
Hence 
, i.e. the value of the derivative given the value of the argument 
numerically equals the tangent of the angle formed by the tangent at a given point with the positive direction of the axis 
.
2.3. Table of basic differentiation formulas.
Power function
|
|
|
|
|
|
|
Exponential function
|
|
|
|
|
logarithmic function
|
|
|
|
|
trigonometric function
|
|
|
|
|
|
|
|
|
|
Inverse trigonometric function
|
|
|
|
|
|
|
|
|
|
2.4. Differentiation rules.
Derivative of 
Derivative of the sum (difference) of functions
Derivative of the product of two functions
The derivative of the quotient of two functions
2.5. Derivative of a complex function.
Let the function 
such that it can be represented as
and 
, where the variable 
is an intermediate argument, then 
The derivative of a complex function is equal to the product of the derivative of the given function with respect to the intermediate argument by the derivative of the intermediate argument with respect to x.
Example1. 
Example2. 
3. Function differential.
Let there be 
, differentiable on some interval 
let it go at
this function has a derivative
,
then you can write
(1),
where 
- an infinitesimal quantity,
because at 
Multiplying all terms of equality (1) by 
we have:
Where 
- b.m.v. higher order.
Value 
is called the differential of the function 
and denoted 
.
3.1. The geometric value of the differential.
Let the function 
.
Fig.2. The geometric meaning of the differential.
.
Obviously, the differential of the function 
is equal to the increment of the ordinate of the tangent at the given point.
3.2. Derivatives and differentials of various orders.
If there 
, then 
is called the first derivative.
The derivative of the first derivative is called the second order derivative and is written 
.
Derivative of the nth order of the function 
is called the derivative of the (n-1) order and is written:
.
The differential of the differential of a function is called the second differential or the second order differential.
.
.
3.3 Solving biological problems using differentiation.
Task1. Studies have shown that the growth of a colony of microorganisms obeys the law 
, where N
– number of microorganisms (in thousands), t
– time (days).
b) Will the population of the colony increase or decrease during this period?
Answer. The colony will grow in size.
Task 2. The water in the lake is periodically tested to control the content of pathogenic bacteria. Through t days after testing, the concentration of bacteria is determined by the ratio
.
When will the minimum concentration of bacteria come in the lake and it will be possible to swim in it?
Solution A function reaches max or min when its derivative is zero.
,
Let's determine max or min will be in 6 days. To do this, we take the second derivative.
Answer: After 6 days there will be a minimum concentration of bacteria.
\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)
Let's explain it easier. For example, \(\log_(2)(8)\) is equal to the power \(2\) must be raised to to get \(8\). From this it is clear that \(\log_(2)(8)=3\).
|
Examples: |
\(\log_(5)(25)=2\) |
because \(5^(2)=25\) |
||
|
\(\log_(3)(81)=4\) |
because \(3^(4)=81\) |
|||
|
\(\log_(2)\)\(\frac(1)(32)\) \(=-5\) |
because \(2^(-5)=\)\(\frac(1)(32)\) |
Argument and base of the logarithm
Any logarithm has the following "anatomy":
The argument of the logarithm is usually written at its level, and the base is written in subscript closer to the sign of the logarithm. And this entry is read like this: "the logarithm of twenty-five to the base of five."
How to calculate the logarithm?
To calculate the logarithm, you need to answer the question: to what degree should the base be raised to get the argument?
for example, calculate the logarithm: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)
a) To what power must \(4\) be raised to get \(16\)? Obviously the second. So:
\(\log_(4)(16)=2\)
\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)
c) To what power must \(\sqrt(5)\) be raised to get \(1\)? And what degree makes any number a unit? Zero, of course!
\(\log_(\sqrt(5))(1)=0\)
d) To what power must \(\sqrt(7)\) be raised to get \(\sqrt(7)\)? In the first - any number in the first degree is equal to itself.
\(\log_(\sqrt(7))(\sqrt(7))=1\)
e) To what power must \(3\) be raised to get \(\sqrt(3)\)? From we know that is a fractional power, and therefore the square root is the power of \(\frac(1)(2)\) .
\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)
Example : Calculate the logarithm \(\log_(4\sqrt(2))(8)\)
Decision :
|
\(\log_(4\sqrt(2))(8)=x\) |
We need to find the value of the logarithm, let's denote it as x. Now let's use the definition of the logarithm: |
|
|
\((4\sqrt(2))^(x)=8\) |
What links \(4\sqrt(2)\) and \(8\)? Two, because both numbers can be represented by twos: |
|
|
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\) |
On the left, we use the degree properties: \(a^(m)\cdot a^(n)=a^(m+n)\) and \((a^(m))^(n)=a^(m\cdot n)\) |
|
|
\(2^(\frac(5)(2)x)=2^(3)\) |
The bases are equal, we proceed to the equality of indicators |
|
|
\(\frac(5x)(2)\) \(=3\) |
|
Multiply both sides of the equation by \(\frac(2)(5)\) |
|
|
The resulting root is the value of the logarithm |
Answer : \(\log_(4\sqrt(2))(8)=1,2\)
Why was the logarithm invented?
To understand this, let's solve the equation: \(3^(x)=9\). Just match \(x\) to make the equality work. Of course, \(x=2\).
Now solve the equation: \(3^(x)=8\). What is x equal to? That's the point.
The most ingenious will say: "X is a little less than two." How exactly is this number to be written? To answer this question, they came up with the logarithm. Thanks to him, the answer here can be written as \(x=\log_(3)(8)\).
I want to emphasize that \(\log_(3)(8)\), as well as any logarithm is just a number. Yes, it looks unusual, but it is short. Because if we wanted to write it as a decimal, it would look like this: \(1.892789260714.....\)
Example : Solve the equation \(4^(5x-4)=10\)
Decision :
|
\(4^(5x-4)=10\) |
\(4^(5x-4)\) and \(10\) cannot be reduced to the same base. So here you can not do without the logarithm. Let's use the definition of the logarithm: |
|
|
\(\log_(4)(10)=5x-4\) |
Flip the equation so x is on the left |
|
|
\(5x-4=\log_(4)(10)\) |
Before us. Move \(4\) to the right. And don't be afraid of the logarithm, treat it like a regular number. |
|
|
\(5x=\log_(4)(10)+4\) |
Divide the equation by 5 |
|
|
\(x=\)\(\frac(\log_(4)(10)+4)(5)\) |
|
Here is our root. Yes, it looks unusual, but the answer is not chosen. |
Answer : \(\frac(\log_(4)(10)+4)(5)\)
Decimal and natural logarithms
As stated in the definition of the logarithm, its base can be any positive number except one \((a>0, a\neq1)\). And among all the possible bases, there are two that occur so often that a special short notation was invented for logarithms with them:
Natural logarithm: a logarithm whose base is the Euler number \(e\) (equal to approximately \(2.7182818…\)), and the logarithm is written as \(\ln(a)\).
I.e, \(\ln(a)\) is the same as \(\log_(e)(a)\)
Decimal logarithm: A logarithm whose base is 10 is written \(\lg(a)\).
I.e, \(\lg(a)\) is the same as \(\log_(10)(a)\), where \(a\) is some number.
Basic logarithmic identity
Logarithms have many properties. One of them is called "Basic logarithmic identity" and looks like this:
| \(a^(\log_(a)(c))=c\) |
This property follows directly from the definition. Let's see how this formula came about.
Recall the short definition of the logarithm:
if \(a^(b)=c\), then \(\log_(a)(c)=b\)
That is, \(b\) is the same as \(\log_(a)(c)\). Then we can write \(\log_(a)(c)\) instead of \(b\) in the formula \(a^(b)=c\) . It turned out \(a^(\log_(a)(c))=c\) - the main logarithmic identity.
You can find the rest of the properties of logarithms. With their help, you can simplify and calculate the values of expressions with logarithms, which are difficult to calculate directly.
Example : Find the value of the expression \(36^(\log_(6)(5))\)
Decision :
Answer : \(25\)
How to write a number as a logarithm?
As mentioned above, any logarithm is just a number. The converse is also true: any number can be written as a logarithm. For example, we know that \(\log_(2)(4)\) is equal to two. Then you can write \(\log_(2)(4)\) instead of two.
But \(\log_(3)(9)\) is also equal to \(2\), so you can also write \(2=\log_(3)(9)\) . Similarly with \(\log_(5)(25)\), and with \(\log_(9)(81)\), etc. That is, it turns out
\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)
Thus, if we need, we can write the two as a logarithm with any base anywhere (even in an equation, even in an expression, even in an inequality) - we just write the squared base as an argument.
It's the same with a triple - it can be written as \(\log_(2)(8)\), or as \(\log_(3)(27)\), or as \(\log_(4)(64) \) ... Here we write the base in the cube as an argument:
\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)
And with four:
\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)
And with minus one:
\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1 )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\)\(...\)
And with one third:
\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)
Any number \(a\) can be represented as a logarithm with base \(b\): \(a=\log_(b)(b^(a))\)
Example : Find the value of an expression \(\frac(\log_(2)(14))(1+\log_(2)(7))\)
Decision :
Answer : \(1\)
Let's start with properties of the logarithm of unity. Its formulation is as follows: the logarithm of unity is equal to zero, that is, log a 1=0 for any a>0 , a≠1 . The proof is straightforward: since a 0 =1 for any a that satisfies the above conditions a>0 and a≠1 , then the proven equality log a 1=0 immediately follows from the definition of the logarithm.
Let's give examples of application of the considered property: log 3 1=0 , lg1=0 and .
Let's move on to the next property: the logarithm of a number equal to the base is equal to one, i.e, log a a=1 for a>0 , a≠1 . Indeed, since a 1 =a for any a , then by the definition of the logarithm log a a=1 .
Examples of using this property of logarithms are log 5 5=1 , log 5.6 5.6 and lne=1 .
For example, log 2 2 7 =7 , log10 -4 =-4 and 
.
Logarithm of the product of two positive numbers x and y is equal to the product of the logarithms of these numbers: log a (x y)=log a x+log a y, a>0 , a≠1 . Let us prove the property of the logarithm of the product. Due to the properties of the degree a log a x+log a y =a log a x a log a y, and since by the main logarithmic identity a log a x =x and a log a y =y , then a log a x a log a y =x y . Thus, a log a x+log a y =x y , whence the required equality follows by the definition of the logarithm.
Let's show examples of using the property of the logarithm of the product: log 5 (2 3)=log 5 2+log 5 3 and 
.
The product logarithm property can be generalized to the product of a finite number n of positive numbers x 1 , x 2 , …, x n as log a (x 1 x 2 ... x n)= log a x 1 + log a x 2 +…+ log a x n . This equality is easily proved.
For example, the natural logarithm of a product can be replaced by the sum of three natural logarithms of the numbers 4 , e , and .
Logarithm of the quotient of two positive numbers x and y is equal to the difference between the logarithms of these numbers. The quotient logarithm property corresponds to a formula of the form , where a>0 , a≠1 , x and y are some positive numbers. The validity of this formula is proved like the formula for the logarithm of the product: since 
, then by the definition of the logarithm .
Here is an example of using this property of the logarithm: 
.
Let's move on to property of the logarithm of degree. The logarithm of a degree is equal to the product of the exponent and the logarithm of the modulus of the base of this degree. We write this property of the logarithm of the degree in the form of a formula: log a b p =p log a |b|, where a>0 , a≠1 , b and p are numbers such that the degree of b p makes sense and b p >0 .
We first prove this property for positive b . The basic logarithmic identity allows us to represent the number b as a log a b , then b p =(a log a b) p , and the resulting expression, due to the power property, is equal to a p log a b . So we arrive at the equality b p =a p log a b , from which, by the definition of the logarithm, we conclude that log a b p =p log a b .
It remains to prove this property for negative b . Here we note that the expression log a b p for negative b makes sense only for even exponents p (since the value of the degree b p must be greater than zero, otherwise the logarithm will not make sense), and in this case b p =|b| p . Then b p =|b| p =(a log a |b|) p =a p log a |b|, whence log a b p =p log a |b| .
For example, 
and ln(-3) 4 =4 ln|-3|=4 ln3 .
It follows from the previous property property of the logarithm from the root: the logarithm of the root of the nth degree is equal to the product of the fraction 1/n and the logarithm of the root expression, that is, 
, where a>0 , a≠1 , n is a natural number greater than one, b>0 .
The proof is based on the equality (see ), which is valid for any positive b , and the property of the logarithm of the degree: 
.
Here is an example of using this property: 
.
Now let's prove conversion formula to the new base of the logarithm kind 
. To do this, it suffices to prove the validity of the equality log c b=log a b log c a . The basic logarithmic identity allows us to represent the number b as a log a b , then log c b=log c a log a b . It remains to use the property of the logarithm of the degree: log c a log a b = log a b log c a. Thus, the equality log c b=log a b log c a is proved, which means that the formula for the transition to a new base of the logarithm is also proved.
Let's show a couple of examples of applying this property of logarithms: and 
.
The formula for moving to a new base allows you to move on to working with logarithms that have a “convenient” base. For example, it can be used to switch to natural or decimal logarithms so that you can calculate the value of the logarithm from the table of logarithms. The formula for the transition to a new base of the logarithm also allows in some cases to find the value of a given logarithm, when the values of some logarithms with other bases are known.
Often used is a special case of the formula for the transition to a new base of the logarithm for c=b of the form 
. This shows that log a b and log b a – . For example, 
.
Also often used is the formula 
, which is useful for finding logarithm values. To confirm our words, we will show how the value of the logarithm of the form is calculated using it. We have 
. To prove the formula 
it is enough to use the transition formula to the new base of the logarithm a: 
.
It remains to prove the comparison properties of logarithms.
Let us prove that for any positive numbers b 1 and b 2 , b 1 log a b 2 , and for a>1, the inequality log a b 1 Finally, it remains to prove the last of the listed properties of logarithms. We confine ourselves to proving its first part, that is, we prove that if a 1 >1 , a 2 >1 and a 1 1 is true log a 1 b>log a 2 b . The remaining statements of this property of logarithms are proved by a similar principle. Let's use the opposite method. Suppose that for a 1 >1 , a 2 >1 and a 1 1 log a 1 b≤log a 2 b is true. By the properties of logarithms, these inequalities can be rewritten as 
and 
respectively, and from them it follows that log b a 1 ≤log b a 2 and log b a 1 ≥log b a 2, respectively. Then, by the properties of powers with the same bases, the equalities b log b a 1 ≥b log b a 2 and b log b a 1 ≥b log b a 2 must be satisfied, that is, a 1 ≥a 2 . Thus, we have arrived at a contradiction to the condition a 1
Bibliography.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. and others. Algebra and the Beginnings of Analysis: A Textbook for Grades 10-11 of General Educational Institutions.
- Gusev V.A., Mordkovich A.G. Mathematics (a manual for applicants to technical schools).
Logarithm of b (b > 0) to base a (a > 0, a ≠ 1) is the exponent to which you need to raise the number a to get b.
The base 10 logarithm of b can be written as log(b), and the logarithm to the base e (natural logarithm) - ln(b).
Often used when solving problems with logarithms:
Properties of logarithms
There are four main properties of logarithms.
Let a > 0, a ≠ 1, x > 0 and y > 0.
Property 1. Logarithm of the product
Logarithm of the product is equal to the sum of logarithms:
log a (x ⋅ y) = log a x + log a y
Property 2. Logarithm of the quotient
Logarithm of the quotient is equal to the difference of logarithms:
log a (x / y) = log a x – log a y
Property 3. Logarithm of the degree
Degree logarithm is equal to the product of the degree and the logarithm:
If the base of the logarithm is in the exponent, then another formula applies:
Property 4. Logarithm of the root
This property can be obtained from the property of the logarithm of the degree, since the root of the nth degree is equal to the power of 1/n:
The formula for going from a logarithm in one base to a logarithm in another base
This formula is also often used when solving various tasks for logarithms:
Special case:
Comparison of logarithms (inequalities)
Suppose we have 2 functions f(x) and g(x) under logarithms with the same bases and there is an inequality sign between them:
To compare them, you first need to look at the base of the logarithms a:
- If a > 0, then f(x) > g(x) > 0
- If 0< a < 1, то 0 < f(x) < g(x)
How to solve problems with logarithms: examples
Tasks with logarithms included in the USE in mathematics for grade 11 in task 5 and task 7, you can find tasks with solutions on our website in the relevant sections. Also, tasks with logarithms are found in the bank of tasks in mathematics. You can find all examples by searching the site.
What is a logarithm
Logarithms have always been considered a difficult topic in the school mathematics course. There are many different definitions of the logarithm, but for some reason most textbooks use the most complex and unfortunate of them.
We will define the logarithm simply and clearly. Let's create a table for this:
So, we have powers of two.
Logarithms - properties, formulas, how to solve
If you take the number from the bottom line, then you can easily find the power to which you have to raise a two to get this number. For example, to get 16, you need to raise two to the fourth power. And to get 64, you need to raise two to the sixth power. This can be seen from the table.
And now - in fact, the definition of the logarithm:
base a of the argument x is the power to which the number a must be raised to get the number x.
Notation: log a x \u003d b, where a is the base, x is the argument, b is actually what the logarithm is equal to.
For example, 2 3 = 8 ⇒ log 2 8 = 3 (the base 2 logarithm of 8 is three because 2 3 = 8). Might as well log 2 64 = 6, because 2 6 = 64.
The operation of finding the logarithm of a number to a given base is called. So let's add a new row to our table:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
Unfortunately, not all logarithms are considered so easily. For example, try to find log 2 5. The number 5 is not in the table, but logic dictates that the logarithm will lie somewhere on the segment. Because 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Such numbers are called irrational: the numbers after the decimal point can be written indefinitely, and they never repeat. If the logarithm turns out to be irrational, it is better to leave it like this: log 2 5, log 3 8, log 5 100.
It is important to understand that the logarithm is an expression with two variables (base and argument). At first, many people confuse where the base is and where the argument is. To avoid annoying misunderstandings, just take a look at the picture:
Before us is nothing more than the definition of the logarithm. Remember: the logarithm is the power, to which you need to raise the base to get the argument. It is the base that is raised to a power - in the picture it is highlighted in red. It turns out that the base is always at the bottom! I tell this wonderful rule to my students at the very first lesson - and there is no confusion.
How to count logarithms
We figured out the definition - it remains to learn how to count logarithms, i.e. get rid of the "log" sign. To begin with, we note that two important facts follow from the definition:
- The argument and base must always be greater than zero. This follows from the definition of the degree by a rational exponent, to which the definition of the logarithm is reduced.
- The base must be different from unity, since a unit to any power is still a unit. Because of this, the question “to what power must one be raised to get two” is meaningless. There is no such degree!
Such restrictions are called valid range(ODZ). It turns out that the ODZ of the logarithm looks like this: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Note that there are no restrictions on the number b (the value of the logarithm) is not imposed. For example, the logarithm may well be negative: log 2 0.5 = −1, because 0.5 = 2 −1 .
However, now we are considering only numerical expressions, where it is not required to know the ODZ of the logarithm. All restrictions have already been taken into account by the compilers of the problems. But when logarithmic equations and inequalities come into play, the DHS requirements will become mandatory. Indeed, in the basis and argument there can be very strong constructions, which do not necessarily correspond to the above restrictions.
Now consider the general scheme for calculating logarithms. It consists of three steps:
- Express the base a and the argument x as a power with the smallest possible base greater than one. Along the way, it is better to get rid of decimal fractions;
- Solve the equation for the variable b: x = a b ;
- The resulting number b will be the answer.
That's all! If the logarithm turns out to be irrational, this will be seen already at the first step. The requirement that the base be greater than one is very relevant: this reduces the likelihood of error and greatly simplifies calculations. Similarly with decimal fractions: if you immediately convert them to ordinary ones, there will be many times less errors.
Let's see how this scheme works with specific examples:
Task. Calculate the logarithm: log 5 25
- Let's represent the base and the argument as a power of five: 5 = 5 1 ; 25 = 52;
- Received an answer: 2.
Let's make and solve the equation:
log 5 25 = b ⇒(5 1) b = 5 2 ⇒5 b = 5 2 ⇒ b = 2;
Task. Calculate the logarithm:
Task. Calculate the logarithm: log 4 64
- Let's represent the base and the argument as a power of two: 4 = 2 2 ; 64 = 26;
- Let's make and solve the equation:
log 4 64 = b ⇒(2 2) b = 2 6 ⇒2 2b = 2 6 ⇒2b = 6 ⇒ b = 3; - Received an answer: 3.
Task. Calculate the logarithm: log 16 1
- Let's represent the base and the argument as a power of two: 16 = 2 4 ; 1 = 20;
- Let's make and solve the equation:
log 16 1 = b ⇒(2 4) b = 2 0 ⇒2 4b = 2 0 ⇒4b = 0 ⇒ b = 0; - Received a response: 0.
Task. Calculate the logarithm: log 7 14
- Let's represent the base and the argument as a power of seven: 7 = 7 1 ; 14 is not represented as a power of seven, because 7 1< 14 < 7 2 ;
- It follows from the previous paragraph that the logarithm is not considered;
- The answer is no change: log 7 14.
A small note on the last example. How to make sure that a number is not an exact power of another number? Very simple - just decompose it into prime factors. If there are at least two distinct factors in the expansion, the number is not an exact power.
Task. Find out if the exact powers of the number are: 8; 48; 81; 35; fourteen.
8 \u003d 2 2 2 \u003d 2 3 - the exact degree, because there is only one multiplier;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 is not an exact power because there are two factors: 3 and 2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - exact degree;
35 = 7 5 - again not an exact degree;
14 \u003d 7 2 - again not an exact degree;
Note also that the prime numbers themselves are always exact powers of themselves.
Decimal logarithm
Some logarithms are so common that they have a special name and designation.
of the x argument is the base 10 logarithm, i.e. the power to which 10 must be raised to obtain x. Designation: lgx.
For example, log 10 = 1; log 100 = 2; lg 1000 = 3 - etc.
From now on, when a phrase like “Find lg 0.01” appears in the textbook, know that this is not a typo. This is the decimal logarithm. However, if you are not used to such a designation, you can always rewrite it:
log x = log 10 x
Everything that is true for ordinary logarithms is also true for decimals.
natural logarithm
There is another logarithm that has its own notation. In a sense, it is even more important than decimal. This is the natural logarithm.
of the x argument is the logarithm to the base e, i.e. the power to which the number e must be raised to get the number x. Designation: lnx.
Many will ask: what is the number e? This is an irrational number, its exact value cannot be found and written down. Here are just the first numbers:
e = 2.718281828459…
We will not delve into what this number is and why it is needed. Just remember that e is the base of the natural logarithm:
ln x = log e x
Thus ln e = 1; log e 2 = 2; ln e 16 = 16 - etc. On the other hand, ln 2 is an irrational number. In general, the natural logarithm of any rational number is irrational. Except, of course, unity: ln 1 = 0.
For natural logarithms, all the rules that are true for ordinary logarithms are valid.
See also:
Logarithm. Properties of the logarithm (power of the logarithm).
How to represent a number as a logarithm?
We use the definition of a logarithm.
The logarithm is an indicator of the power to which the base must be raised to get the number under the sign of the logarithm.
Thus, in order to represent a certain number c as a logarithm to the base a, it is necessary to put a degree under the sign of the logarithm with the same base as the base of the logarithm, and write this number c into the exponent:
In the form of a logarithm, you can represent absolutely any number - positive, negative, integer, fractional, rational, irrational:
In order not to confuse a and c in stressful conditions of a test or exam, you can use the following rule to remember:
what is below goes down, what is above goes up.
For example, you want to represent the number 2 as a logarithm to base 3.
We have two numbers - 2 and 3. These numbers are the base and the exponent, which we will write under the sign of the logarithm. It remains to determine which of these numbers should be written down, in the base of the degree, and which - up, in the exponent.
The base 3 in the record of the logarithm is at the bottom, which means that when we represent the deuce as a logarithm to the base of 3, we will also write 3 down to the base.
2 is higher than 3. And in the notation of the degree, we write the two above the three, that is, in the exponent:
Logarithms. First level.
Logarithms
logarithm positive number b by reason a, where a > 0, a ≠ 1, is the exponent to which the number must be raised. a, To obtain b.
Definition of logarithm can be briefly written like this:
This equality is valid for b > 0, a > 0, a ≠ 1. He is usually called logarithmic identity.
The action of finding the logarithm of a number is called logarithm.
Properties of logarithms:
The logarithm of the product:
Logarithm of the quotient from division:
Replacing the base of the logarithm:
Degree logarithm:
root logarithm:
Logarithm with power base:
Decimal and natural logarithms.
Decimal logarithm numbers call the base 10 logarithm of that number and write lg b
natural logarithm numbers call the logarithm of this number to the base e, where e is an irrational number, approximately equal to 2.7. At the same time, they write ln b.
Other Notes on Algebra and Geometry
Basic properties of logarithms
Basic properties of logarithms
Logarithms, like any number, can be added, subtracted and converted in every possible way. But since logarithms are not quite ordinary numbers, there are rules here, which are called basic properties.
These rules must be known - no serious logarithmic problem can be solved without them. In addition, there are very few of them - everything can be learned in one day. So let's get started.
Addition and subtraction of logarithms
Consider two logarithms with the same base: log a x and log a y. Then they can be added and subtracted, and:
- log a x + log a y = log a (x y);
- log a x - log a y = log a (x: y).
So, the sum of the logarithms is equal to the logarithm of the product, and the difference is the logarithm of the quotient. Please note: the key point here is - same grounds. If the bases are different, these rules do not work!
These formulas will help calculate the logarithmic expression even when its individual parts are not considered (see the lesson "What is a logarithm"). Take a look at the examples and see:
log 6 4 + log 6 9.
Since the bases of logarithms are the same, we use the sum formula:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Task. Find the value of the expression: log 2 48 − log 2 3.
The bases are the same, we use the difference formula:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Task. Find the value of the expression: log 3 135 − log 3 5.
Again, the bases are the same, so we have:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
As you can see, the original expressions are made up of "bad" logarithms, which are not considered separately. But after transformations quite normal numbers turn out. Many tests are based on this fact. Yes, control - similar expressions in all seriousness (sometimes - with virtually no changes) are offered at the exam.
Removing the exponent from the logarithm
Now let's complicate the task a little. What if there is a degree in the base or argument of the logarithm? Then the exponent of this degree can be taken out of the sign of the logarithm according to the following rules:
It is easy to see that the last rule follows their first two. But it's better to remember it anyway - in some cases it will significantly reduce the amount of calculations.
Of course, all these rules make sense if the ODZ logarithm is observed: a > 0, a ≠ 1, x > 0. And one more thing: learn to apply all formulas not only from left to right, but also vice versa, i.e. you can enter the numbers before the sign of the logarithm into the logarithm itself.
How to solve logarithms
This is what is most often required.
Task. Find the value of the expression: log 7 49 6 .
Let's get rid of the degree in the argument according to the first formula:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Task. Find the value of the expression:
Note that the denominator is a logarithm whose base and argument are exact powers: 16 = 2 4 ; 49 = 72. We have:
I think the last example needs clarification. Where have logarithms gone? Until the very last moment, we work only with the denominator. They presented the base and the argument of the logarithm standing there in the form of degrees and took out the indicators - they got a “three-story” fraction.
Now let's look at the main fraction. The numerator and denominator have the same number: log 2 7. Since log 2 7 ≠ 0, we can reduce the fraction - 2/4 will remain in the denominator. According to the rules of arithmetic, the four can be transferred to the numerator, which was done. The result is the answer: 2.
Transition to a new foundation
Speaking about the rules for adding and subtracting logarithms, I specifically emphasized that they only work with the same bases. What if the bases are different? What if they are not exact powers of the same number?
Formulas for transition to a new base come to the rescue. We formulate them in the form of a theorem:
Let the logarithm log a x be given. Then for any number c such that c > 0 and c ≠ 1, the equality is true:
In particular, if we put c = x, we get:
It follows from the second formula that it is possible to interchange the base and the argument of the logarithm, but in this case the whole expression is “turned over”, i.e. the logarithm is in the denominator.
These formulas are rarely found in ordinary numerical expressions. It is possible to evaluate how convenient they are only when solving logarithmic equations and inequalities.
However, there are tasks that cannot be solved at all except by moving to a new foundation. Let's consider a couple of these:
Task. Find the value of the expression: log 5 16 log 2 25.
Note that the arguments of both logarithms are exact exponents. Let's take out the indicators: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
Now let's flip the second logarithm:
Since the product does not change from permutation of factors, we calmly multiplied four and two, and then figured out the logarithms.
Task. Find the value of the expression: log 9 100 lg 3.
The base and argument of the first logarithm are exact powers. Let's write it down and get rid of the indicators:
Now let's get rid of the decimal logarithm by moving to a new base:
Basic logarithmic identity
Often in the process of solving it is required to represent a number as a logarithm to a given base.
In this case, the formulas will help us:
In the first case, the number n becomes the exponent in the argument. The number n can be absolutely anything, because it's just the value of the logarithm.
The second formula is actually a paraphrased definition. It's called like this:
Indeed, what will happen if the number b is raised to such a degree that the number b in this degree gives the number a? That's right: this is the same number a. Read this paragraph carefully again - many people “hang” on it.
Like the new base conversion formulas, the basic logarithmic identity is sometimes the only possible solution.
Task. Find the value of the expression:
Note that log 25 64 = log 5 8 - just took out the square from the base and the argument of the logarithm. Given the rules for multiplying powers with the same base, we get:
If someone is not in the know, this was a real task from the Unified State Examination 🙂
Logarithmic unit and logarithmic zero
In conclusion, I will give two identities that are difficult to call properties - rather, these are consequences from the definition of the logarithm. They are constantly found in problems and, surprisingly, create problems even for "advanced" students.
- log a a = 1 is. Remember once and for all: the logarithm to any base a from that base itself is equal to one.
- log a 1 = 0 is. The base a can be anything, but if the argument is one, the logarithm is zero! Because a 0 = 1 is a direct consequence of the definition.
That's all the properties. Be sure to practice putting them into practice! Download the cheat sheet at the beginning of the lesson, print it out and solve the problems.
derived from its definition. And so the logarithm of the number b by reason a defined as the exponent to which a number must be raised a to get the number b(the logarithm exists only for positive numbers).
From this formulation it follows that the calculation x=log a b, is equivalent to solving the equation ax=b. For example, log 2 8 = 3 because 8 = 2 3 . The formulation of the logarithm makes it possible to justify that if b=a c, then the logarithm of the number b by reason a equals with. It is also clear that the topic of the logarithm is closely related to the topic of the power of a number.
With logarithms, as with any numbers, you can perform operations of addition, subtraction and transform in every possible way. But in view of the fact that logarithms are not quite ordinary numbers, their own special rules apply here, which are called basic properties.
Addition and subtraction of logarithms.
Take two logarithms with the same base: log x and log a y. Then remove it is possible to perform addition and subtraction operations:
log a x+ log a y= log a (x y);
log a x - log a y = log a (x:y).
log a(x 1 . x 2 . x 3 ... x k) = log x 1 + log x 2 + log x 3 + ... + log a x k.
From quotient logarithm theorems one more property of the logarithm can be obtained. It is well known that log a 1= 0, therefore,
log a 1 /b= log a 1 - log a b= -log a b.
So there is an equality:
log a 1 / b = - log a b.
Logarithms of two mutually reciprocal numbers on the same basis will differ from each other only in sign. So:
Log 3 9= - log 3 1 / 9 ; log 5 1 / 125 = -log 5 125.
We also recommend
Loading...