Калькулятор неравенств с решением онлайн. Линейные неравенства

Неравенство – это числовое соотношение, иллюстрирующее величину чисел относительно друг друга. Неравенства широко используются при поиске величин в прикладных науках. Наш калькулятор поможет вам разобраться с такой непростой темой, как решение линейных неравенств.

Что такое неравенство

Неравные соотношения в реальной жизни соотносятся с постоянным сравнением различных объектов: выше или ниже, дальше или ближе, тяжелее или легче. Интуитивно или зрительно мы можем понять, что один объект больше, выше или тяжелее другого, однако фактически речь всегда идет о сравнении чисел, которые характеризуют соответствующие величины. Сравнивать объекты можно по любому признаку и в любом случае мы можем составить числовое неравенство.

Если неизвестные величины при конкретных условиях равны, то для их численного определения мы составляем уравнение. Если же нет, то вместо знака «равно» мы можем указать любое другое соотношение между этими величинами. Два числа или математических объекта могут быть больше «>», меньше «<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.

Знаки неравенств в их современном виде придумал британский математик Томас Гарриот, который в 1631 году выпустил книгу о неравных соотношениях. Знаки больше «>» и меньше «<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.

Решение неравенств

Неравенства, как и уравнения, бывают разных типов. Линейные, квадратные, логарифмические или показательные неравные соотношения развязываются различными методами. Однако вне зависимости от метода, любое неравенство вначале требуется привести к стандартному виду. Для этого используются тождественные преобразования, идентичные видоизменениям равенств.

Тождественные преобразования неравенств

Такие трансформации выражений очень похожи на привидение уравнений, однако они имеют нюансы, которые важно учитывать при развязывании неравенств.

Первое тождественное преобразование идентично аналогичной операции с равенствами. К обеим сторонам неравного соотношения можно прибавить или отнять одно и то же число или выражение с неизвестным иксом, при этом знак неравенства останется прежним. Чаще всего этот метод применяется в упрощенной форме как перенос членов выражения через знак неравенства со сменой знака числа на противоположный. Имеется в виду смена знака самого члена, то есть +R при переносе через любой знак неравенства изменится на – R и наоборот.

Второе преобразование имеет два пункта:

Обе стороны неравного соотношения разрешается умножить или разделить на одно и то же положительное число. Знак самого неравенства при этом не изменится.
Обе стороны неравенства разрешается разделить или умножить на одно и то же отрицательное число. Знак самого неравенства изменится на противоположный.

Второе тождественное преобразование неравенств имеет серьезные различия с видоизменением уравнений. Во-первых, при умножении/делении на отрицательное число знак неравного выражения всегда изменяется на обратный. Во-вторых, разделить или умножить части отношения разрешается только на число, а не на любое выражение, содержащее неизвестное. Дело в том, что мы не можем точно знать, число больше или меньше нуля скрывается за неизвестным, поэтому второе тождественное преобразование применяется к неравенствам исключительно с числами. Рассмотрим эти правила на примерах.

Примеры развязывания неравенств

В заданиях по алгебре встречаются самые разные задания на тему неравенств. Пусть нам дано выражение:

6x − 3(4x + 1) > 6.

Для начала раскроем скобки и перенесем все неизвестные влево, а все числа – вправо.

6x − 12x > 6 + 3

Нам требуется поделить обе части выражения на −6, поэтому при нахождении неизвестного икса знак неравенства изменится на противоположный.

При решении этого неравенства мы использовали оба тождественных преобразования: перенесли все числа справа от знака и разделили обе стороны соотношения на отрицательное число.

Наша программа представляет собой калькулятор решения числовых неравенств, которые не содержат неизвестных. В программу заложены следующие теоремы для соотношений трех чисел:

если A < B то A–C< B–C;
если A > B, то A–C > B–C.

Вместо вычитания членов A–C вы можете указать любое арифметическое действие: сложение, умножение или деление. Таким образом, калькулятор автоматически представит неравенства сумм, разностей, произведений или дробей.

Заключение

В реальной жизни неравенства встречаются также часто, как и уравнения. Естественно, что в быту знания о разрешении неравенств могут и не понадобиться. Однако в прикладных науках неравенства и их системы находят широкое применение. К примеру, различные исследования проблем глобальной экономики сводятся к составлению и развязыванию систем линейных или квадратных неравенств, а некоторые неравные отношения служат однозначным способом доказательства существования определенных объектов. Пользуйтесь нашими программами для решения линейных неравенств или проверки собственных выкладок.

Вида ах 2 + bх + 0 0, где (вместо знака > может быть, разумеется, любой другой знак неравенства). Всеми необходимыми для решения таких неравенств фактами теории мы с вами располагаем, в чем сейчас и убедимся.

Пример 1 . Решить неравенство:

а) х 2 - 2х - 3 >0; б) х 2 - 2х - 3 < 0;
в) х 2 - 2х - 3 > 0; г) х 2 - 2х - 3 < 0.
Решение,

а) Рассмотрим параболу у = х 2 - 2х - 3, изображенную на рис. 117.

Решить неравенство х 2 - 2х - 3 > 0 - это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны.

Замечаем, что у > 0, т. е. график функции расположен выше оси х, при х < -1 или при х > 3.

Значит, решениями неравенства служат все точки открытого луча (- 00 , - 1), а также все точки открытого луча (3, +00).

Используя знак U (знак объединения множеств), ответ можно записать так: (-00 , - 1) U (3, +00). Впрочем, ответ можно записать и так: х < - 1; х > 3.

б) Неравенство х 2 - 2х - 3 < 0, или у < 0, где у = х 2 - 2х - 3, также можно решить с помощью рис. 117: график расположен ниже оси х, если -1 < х < 3. Поэтому решениями данного неравенства служат все точки интервала (- 1, 3).

в) Неравенство х 2 - 2х - 3 > 0 отличается от неравенства х 2 - 2х - 3 > 0 тем, что в ответ надо включить и корни уравнения х 2 - 2х - 3 = 0, т. е. точки х = -1

и х = 3. Таким образом, решениями данного нестрогого неравенства являются все точки луча (-00 , - 1], а также все точки луча .

Практичные математики обычно говорят так: зачем нам, решая неравенство ах 2 + bх + с > 0, аккуратно строить параболу график квадратичной функции

у = ах 2 + bх + с (как это было сделано в примере 1)? Достаточно сделать схематический набросок графика, для чего следует лишь найти корни квадратного трехчлена (точки пересечения параболы с осью х) и определить, куда направлены ветви параболы - вверх или вниз. Этот схематический набросок даст наглядное истолкование решению неравенства.

Пример 2. Решить неравенство - 2х 2 + Зх + 9 < 0.
Решение.

1) Найдем корни квадратного трехчлена - 2х 2 + Зх + 9: х 1 = 3; х 2 = - 1,5.

2) Парабола, служащая графиком функции у = -2х 2 + Зх + 9, пересекает ось х в точках 3 и - 1,5, а ветви параболы направлены вниз, поскольку старший коэффициент - отрицательное число - 2. На рис. 118 представлен набросок графика.

3) Используя рис. 118, делаем вывод: у < 0 на тех промежутках оси х, где график расположен ниже оси х, т.е. на открытом луче (-оо, -1,5) или на открытом луче C, +оо).
Ответ: х < -1,5; х > 3.

Пример 3. Решить неравенство 4х 2 - 4х + 1 < 0.
Решение.

1) Из уравнения 4х 2 - 4х + 1 = 0 находим .

2) Квадратный трехчлен имеет один корень ; это значит, что парабола, служащая графиком квадратного трехчлена, не пересекает ось х, а касается ее в точке . Ветви параболы направлены вверх (рис. 119.)

3) С помощью геометрической модели, представленной на рис. 119, устанавливаем, что заданное неравенство выполняется только в точке , поскольку при всех других значениях х ординаты графика положительны.
Ответ: .
Вы, наверное, заметили, что фактически в примерах 1, 2, 3 использовался вполне определенный алгоритм решения квадратных неравенств, оформим его.

Алгоритм решения квадратного неравенства ах 2 + bх + 0 0 (ах 2 + bх + с < 0)

На первом шаге этого алгоритма требуется найти корни квадратного трехчлена. Но ведь корни могут и не существовать, что же делать? Тогда алгоритм неприменим, значит, надо рассуждать как-то по-другому. Ключ к этим рассуждениям дают следующие теоремы.

Иными словами, если D < 0, а > 0, то неравенство ах 2 + bх + с > 0 выполняется при всех х; напротив, неравенство ах 2 + bх + с < 0 не имеет решений.
Доказательство. Графиком функции у = ах 2 + bх + с является парабола, ветви которой направлены вверх (поскольку а > 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 120. Видим, что при всех х график расположен выше оси х, а это значит, что при всех х выполняется неравенство ах 2 + bх + с > 0, что и требовалось доказать.

Иными словами, если D < 0, а < 0, то неравенство ах 2 + bх + с < 0 выполняется при всех х; напротив, неравенство ах 2 + bх + с > 0 не имеет решений.

Доказательство. Графиком функции у = ах 2 + bх +с является парабола, ветви которой направлены вниз (поскольку а < 0) и которая не пересекает ось х, так как корней у квадратного трехчлена по условию нет. График представлен на рис. 121. Видим, что при всех х график расположен ниже оси х, а это значит, что при всех х выполняется неравенство ах 2 + bх + с < 0, что и требовалось доказать.

Пример 4 . Решить неравенство:

а) 2х 2 - х + 4 >0; б) -х 2 + Зх - 8 >0.

а) Найдем дискриминант квадратного трехчлена 2х 2 - х + 4. Имеем D = (-1) 2 - 4 2 4 = - 31 < 0.
Старший коэффициент трехчлена (число 2) положителен.

Значит, по теореме 1, при всех х выполняется неравенство 2x 2 - х + 4 > 0, т. е. решением заданного неравенства служит вся (-00 , + 00).

б) Найдем дискриминант квадратного трехчлена - х 2 + Зх - 8. Имеем D = З2 - 4 (- 1) (- 8) = - 23 < 0. Старший коэффициент трехчлена (число - 1) отрицателен. Следовательно, по теореме 2, при всех х выполняется неравенство - х 2 + Зx - 8 < 0. Это значит, что неравенство - х 2 + Зх - 8 0 не выполняется ни при каком значении х, т. е. заданное неравенство не имеет решений.

Ответ: а) (-00 , + 00); б) нет решений.

В следующем примере мы познакомимся еще с одним способом рассуждений, который применяется при решении квадратных неравенств.

Пример 5. Решить неравенство Зх 2 - 10х + 3 < 0.
Решение. Разложим квадратный трехчлен Зx 2 - 10x + 3 на множители. Корнями трехчлена являются числа 3 и , поэтому воспользовавшись ах 2 + bх + с = а (х - x 1)(x - х 2),получим Зx 2 - 10х + 3 = 3(х - 3) (х - )
Отметим на числовой прямой корни трехчлена: 3 и (рис. 122).

Пусть х > 3; тогда x-3>0 и x->0, а значит, и произведение 3(х - 3)(х - ) положительно. Далее, пусть < х < 3; тогда x-3< 0, а х- >0. Следовательно, произведение 3(х-3)(х-) отрицательно. Пусть, наконец, х <; тогда x-3< 0 и x- < 0. Но в таком случае произведение
3(x -3)(x -) положительно.

Подводя итог рассуждениям, приходим к выводу: знаки квадратного трехчлена Зx 2 - 10х + 3 изменяются так, как показано на рис. 122. Нас же интересует, при каких х квадратный трехчлен принимает отрицательные значения. Из рис. 122 делаем вывод: квадратный трехчлен Зx 2 - 10х + 3 принимает отрицательные значения для любого значения х из интервала (, 3)
Ответ (, 3), или < х < 3.

Замечание. Метод рассуждений, который мы применили в примере 5, обычно называют методом интервалов (или методом промежутков). Он активно используется в математике для решения рациональных неравенств. В 9-м классе мы изучим метод интервалов более детально.

Пример 6 . При каких значениях параметра р квадратное уравнение х 2 - 5х + р 2 = 0:
а) имеет два различных корня;

б) имеет один корень;

в) не имеет -корней?

Решение. Число корней квадратного уравнения зависит от знака его дискриминанта D. В данном случае находим D = 25 - 4р 2 .

а) Квадратное уравнение имеет два различных корня, если D>0, значит, задача сводится к решению неравенства 25 - 4р 2 > 0. Умножим обе части этого неравенства на -1 (не забыв изменить при этом знак неравенства). Получим равносильное неравенство 4р 2 - 25 < 0. Далее имеем 4 (р - 2,5) (р + 2,5) < 0.

Знаки выражения 4(р - 2,5) (р + 2,5) указаны на рис. 123.

Делаем вывод, что неравенство 4(р - 2,5)(р + 2,5) < 0 выполняется для всех значений р из интервала (-2,5; 2,5). Именно при этих значениях параметра р данное квадратное уравнение имеет два различных корня.

б) квадратное уравнение имеет один корень, если D - 0.
Как мы установили выше, D = 0 при р = 2,5 или р = -2,5.

Именно при этих значениях параметра р данное квадратное уравнение имеет только один корень.

в) Квадратное уравнение не имеет корней, если D < 0. Решим неравенство 25 - 4р 2 < 0.

Получаем 4р 2 - 25 > 0; 4 (р-2,5)(р + 2,5)>0, откуда (см. рис. 123) р < -2,5; р > 2,5. При этих значениях параметра р данное квадратное уравнение не имеет корней.

Ответ: а) при р (-2,5, 2,5);

б) при р = 2,5 илир = -2,5;
в) при р < - 2,5 или р > 2,5.

Мордкович А. Г., Алгебра . 8 кл.: Учеб. для общеобразоват. учреждений.- 3-е изд., доработ. - М.: Мнемозина, 2001. - 223 с: ил.

Помощь школьнику онлайн , Математика для 8 класса скачать , календарно-тематическое планирование

см. также Решение задачи линейного программирования графически , Каноническая форма задач линейного программирования

Система ограничений такой задачи состоит из неравенств от двух переменных:
и целевая функция имеет вид F = C 1 x + C 2 y , которую необходимо максимизировать.

Ответим на вопрос: какие пары чисел ( x ; y ) являются решениями системы неравенств, т. е. удовлетворяют каждому из неравенств одновременно? Другими словами, что значит решить систему графически?
Предварительно необходимо понять, что является решением одного линейного неравенства с двумя неизвестными.
Решить линейное неравенство с двумя неизвестными – это значит определить все пары значений неизвестных, при которых неравенство выполняется.
Например, неравенству 3x – 5 y ≥ 42 удовлетворяют пары (x , y ) : (100, 2); (3, –10) и т. д. Задача состоит в нахождении всех таких пар.
Рассмотрим два неравенства: ax + by ≤ c , ax + by ≥ c . Прямая ax + by = c делит плоскость на две полуплоскости так, что координаты точек одной из них удовлетворяют неравенству ax + by >c , а другой неравенству ax + +by <c .
Действительно, возьмем точку с координатой x = x 0 ; тогда точка, лежащая на прямой и имеющая абсциссу x 0 , имеет ординату

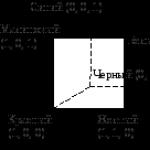
Пусть для определенности a < 0, b >0, c >0. Все точки с абсциссой x 0 , лежащие выше P (например, точка М ), имеют y M >y 0 , а все точки, лежащие ниже точки P , с абсциссой x 0 , имеют y N <y 0 . Поскольку x 0 –произвольная точка, то всегда с одной стороны от прямой будут находиться точки, для которых ax + by > c , образующие полуплоскость, а с другой стороны – точки, для которых ax + by < c .

Рисунок 1

Знак неравенства в полуплоскости зависит от чисел a , b , c .
Отсюда вытекает следующий способ графического решения систем линейных неравенств от двух переменных. Для решения системы необходимо:

Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.

Эта область может оказаться пустой, тогда система неравенств не имеет решений, несовместна. В противном случае говорят, что система совместна.
Решений может быть конечное число и бесконечное множество. Область может представлять собой замкнутый многоугольник или же быть неограниченной.

Рассмотрим три соответствующих примера.

Пример 1. Решить графически систему:
x + y – 1 ≤ 0;
–2 x – 2y + 5 ≤ 0.

рассмотрим уравнения x+y–1=0 и –2x–2y+5=0 , соответствующие неравенствам;
построим прямые, задающиеся этими уравнениями.

Рисунок 2

Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим x + y– 1 0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2x – 2y + 5≥ 0, а нас спрашивали, где –2x – 2y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.

Пример 2. Найти графически решения системы неравенств:

Рисунок 3
1. Выпишем уравнения, соответствующие неравенствам, и построим прямые.
x + 2y – 2 = 0

x	2	0
y	0	1

y – x – 1 = 0

x	0	2
y	1	3

y + 2 = 0;
y = –2.
2. Выбрав точку (0; 0), определим знаки неравенств в полуплоскостях:
0 + 2 ∙ 0 – 2 ≤ 0, т.е. x + 2y – 2 ≤ 0 в полуплоскости ниже прямой;
0 – 0 – 1 ≤ 0, т.е. y –x – 1 ≤ 0 в полуплоскости ниже прямой;
0 + 2 =2 ≥ 0, т.е. y + 2 ≥ 0 в полуплоскости выше прямой.
3. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником. Нетрудно найти вершины области, как точки пересечения соответствующих прямых

Таким образом, А (–3; –2), В (0; 1), С (6; –2).

Рассмотрим еще один пример, в котором получившаяся область решения системы не ограничена.

Решение неравенств онлайн

Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения .

Не важно каким является неравенство – строгим () или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).

Поясним что означает решить неравенство?

После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!

Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?

Как решать неравенства?

Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.

Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.

Как правильно записывать решение неравенства?

Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?

Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.

Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.

Важный момент

Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.

Например, у неравенства |x|≤0 всего одно решение – это точка 0.

А у неравенства |x|

Для чего нужен калькулятор неравенств?

Калькулятор неравенств выдает правильный итоговый ответ. При этом в большинстве случаев приводится иллюстрация числовой оси или плоскости. Видно, входят ли границы интервалов в решение или нет – точки отображаются закрашенными или проколотыми.

Благодаря онлайн калькулятору неравенств можно проверить правильно ли вы нашли корни уравнения, отметили их на числовой оси и проверили на интервалах (и границах) выполнение условия неравенства?

Если ваш ответ расходится с ответом калькулятора, то однозначно нужно перепроверить свое решение и выявить допущенную ошибку.

Неравенство это выражение с, ≤, или ≥. Например, 3x - 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно. Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений . Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .

Линейные неравенства

Принципы решения неравенств аналогичны принципам решения уравнений.

Принципы решения неравенств
Для любых вещественных чисел a, b, и c :
Принцип прибавления неравенств : Если a Принцип умножения для неравенств : Если a 0 верно, тогда ac Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.

Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами .

Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x - 5 b) 13 - 7x ≥ 10x - 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть {x|x
Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x - 5 и y 2 = 6 - 2x. Тогда отсюда видно, что для x
Множеством решений есть {x|x ≤ 1}, или (-∞, 1]. График множества решений изображён ниже.

Двойные неравенства

Когда два неравенства соединены словом и , или , тогда формируется двойное неравенство . Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым , потому что в нём использовано и . Запись -3 Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.

Пример 2 Решите -3 Решение У нас есть

Множество решений {x|x ≤ -1 или x > 3}. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.

Для проверки, нарисуем y 1 = 2x - 5, y 2 = -7, и y 3 = 1. Заметьте, что для {x|x ≤ -1 или x > 3}, y 1 ≤ y 2 или y 1 > y 3 .

Неравенства с абсолютным значением (модулем)

Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x| |x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.

Например,
|x| |y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.

Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2| b) |5 - 2x| ≥ 1

Решение
a) |3x + 2|

Множеством решением есть {x|-7/3