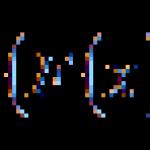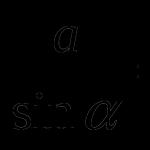Antiderivativlar to'plamini qanday topish mumkin. Sinfdan tashqari dars - Antiderivativ

Antiderivativning ta'rifi.

f(x) funksiyaning (a; b) oraliqdagi anti hosilasi F(x) funksiya bo‘lib, berilgan oraliqdan istalgan x uchun tenglik bajariladi.

Agar doimiy S ning hosilasi nolga teng ekanligini hisobga olsak, tenglik to'g'ri bo'ladi. . Shunday qilib, f(x) funksiya ixtiyoriy doimiy C uchun F(x)+C antiderivativlar to‘plamiga ega va bu antiderivativlar bir-biridan ixtiyoriy doimiy qiymat bilan farqlanadi.

Noaniq integralning ta'rifi.

f(x) funksiyaning butun anti hosilalari to'plami bu funktsiyaning noaniq integrali deb ataladi va belgilanadi. .

ifoda deyiladi integral, va f(x) – integral funktsiyasi. Integrand f(x) funksiyaning differentsialini ifodalaydi.

Noma'lum funktsiyaning differentsialini hisobga olgan holda topish harakati deyiladi noaniq integrasiya, chunki integrasiya natijasi bitta F(x) funksiya emas, balki uning F(x)+C ga qarshi hosilalari to‘plamidir.

Hosilning xossalariga asoslanib, formulalash va isbotlash mumkin noaniq integralning xossalari(antiderivativning xususiyatlari).

Aniqlik uchun noaniq integralning birinchi va ikkinchi xossalarining oraliq tengliklari keltirilgan.

Uchinchi va toʻrtinchi xossalarni isbotlash uchun tengliklarning oʻng tomonlarining hosilalarini topish kifoya:

Bu hosilalar integrallarga teng bo'lib, bu birinchi xususiyat tufayli dalildir. U oxirgi o'tishlarda ham qo'llaniladi.

Shunday qilib, integratsiya muammosi differensiallash muammosiga teskari masala bo'lib, bu muammolar o'rtasida juda yaqin bog'liqlik mavjud:

birinchi xususiyat integratsiyani tekshirish imkonini beradi. Amalga oshirilgan integratsiyaning to'g'riligini tekshirish uchun olingan natijaning hosilasini hisoblash kifoya. Agar differentsiallash natijasida olingan funksiya integrandaga teng bo'lib chiqsa, bu integrasiya to'g'ri amalga oshirilganligini bildiradi;
noaniq integralning ikkinchi xossasi funksiyaning ma'lum differensialidan uning anti hosilasini topish imkonini beradi. Noaniq integrallarni to'g'ridan-to'g'ri hisoblash ushbu xususiyatga asoslanadi.

Keling, bir misolni ko'rib chiqaylik.

Misol.

X = 1 da qiymati bir ga teng funksiyaning anti hosilasi topilsin.

Yechim.

Biz buni differentsial hisobdan bilamiz (asosiy elementar funksiyalarning hosilalari jadvaliga qarang). Shunday qilib, . Ikkinchi mulk bo'yicha . Ya'ni, bizda ko'plab antiderivativlar mavjud. x = 1 uchun biz qiymatni olamiz. Shartga ko'ra, bu qiymat birga teng bo'lishi kerak, shuning uchun C = 1. Kerakli antiderivativ shaklni oladi.

Misol.

Noaniq integralni toping va natijani farqlash orqali tekshiring.

Yechim.

Trigonometriyadan ikki burchakli sinus formulasidan foydalanish , Shunung uchun

Antiderivativ funktsiya f(x) orasida (a; b) bu funksiya deyiladi F(x), bu tenglik har qanday uchun amal qiladi X berilgan oraliqdan.

Agar doimiyning hosilasi ekanligini hisobga olsak BILAN nolga teng bo'lsa, tenglik to'g'ri bo'ladi. Shunday qilib, funktsiya f(x) ko'plab ibtidoiylarga ega F(x)+C, ixtiyoriy doimiy uchun BILAN, va bu antiderivativlar bir-biridan ixtiyoriy doimiy qiymat bilan farqlanadi.

Noaniq integralning ta'rifi.

Antiderivativ funktsiyalarning butun to'plami f(x) bu funksiyaning noaniq integrali deyiladi va belgilanadi .

ifoda deyiladi integral, A f(x) – integral funktsiyasi. Integrand funksiyaning differentsialini ifodalaydi f(x).

Noma'lum funktsiyaning differentsialini hisobga olgan holda topish harakati deyiladi noaniq integratsiya, chunki integratsiya natijasi bir nechta funktsiyadir F(x), va uning ibtidoiylari to'plami F(x)+C.

Noaniq integralning geometrik ma'nosi. Antiderivativ D(x) ning grafigi integral egri chiziq deyiladi. X0y koordinatalar sistemasida berilgan funksiyaning barcha anti hosilalari grafiklari C doimiysi qiymatiga bog’liq bo’lgan va bir-biridan 0y o’qi bo’ylab parallel siljish orqali olinadigan egri chiziqlar turkumini ifodalaydi. Yuqorida muhokama qilingan misol uchun bizda:

J 2 x^x = x2 + C.

Antiderivativlar oilasi (x + C) geometrik ravishda parabolalar to'plami bilan izohlanadi.

Agar antiderivativlar turkumidan birini topish kerak bo'lsa, u holda C konstantasini aniqlash imkonini beruvchi qo'shimcha shartlar o'rnatiladi. Odatda, bu maqsadda dastlabki shartlar o'rnatiladi: x = x0 argumenti bo'lganda, funktsiya D qiymatiga ega bo'ladi. (x0) = y0.

Misol. y = 2 x funktsiyaning x0 = 1 da 3 qiymatini oladigan anti hosilalaridan biri ekanligini topish talab qilinadi.

Kerakli antiderivativ: D(x) = x2 + 2.

Yechim. ^2x^x = x2 + C; 12 + C = 3; C = 2.

2. Noaniq integralning asosiy xossalari

1. Noaniq integralning hosilasi integral funksiyaga teng:

2. Noaniq integralning differensiali integrasiya ifodasiga teng:

3. Muayyan funksiya differensialining noaniq integrali shu funksiyaning o‘zi va ixtiyoriy doimiyning yig‘indisiga teng:

4. Integral belgisidan doimiy koeffitsientni chiqarish mumkin:

5. Yig‘indining (farq) integrali integrallarning yig‘indisiga (farqiga) teng:

6. Mulk 4 va 5 xossalarning birikmasidir:

7. Noaniq integralning o'zgarmaslik xossasi:

Agar , Bu

8. Mulk:

Agar , Bu

Aslida, bu xususiyat o'zgaruvchan o'zgarish usuli yordamida integratsiyaning alohida holati bo'lib, keyingi bo'limda batafsilroq muhokama qilinadi.

Keling, bir misolni ko'rib chiqaylik:

3. Integratsiya usuli bunda berilgan integral integralni (yoki ifodani) bir xil o'zgartirishlar va noaniq integralning xossalarini qo'llash orqali bir yoki bir nechta jadval integrallariga keltiriladi, deyiladi. to'g'ridan-to'g'ri integratsiya. Ushbu integralni jadvalga keltirishda ko'pincha quyidagi differentsial o'zgarishlar qo'llaniladi (operatsiya " differentsial belgiga obuna bo'lish»):

Umuman, f’(u)du = d(f(u)). Bu (formula ko'pincha integrallarni hisoblashda qo'llaniladi.

Integralni toping

Yechim. Keling, integralning xossalaridan foydalanamiz va bu integralni bir nechta jadvalga keltiramiz.

4. Almashtirish usuli bilan integratsiya.

Usulning mohiyati shundan iboratki, biz yangi o'zgaruvchini kiritamiz, bu o'zgaruvchi orqali integratsiyani ifodalaymiz va natijada biz integralning jadvalli (yoki oddiyroq) ko'rinishiga kelamiz.

Ko'pincha trigonometrik funktsiyalar va funktsiyalarni radikallar bilan integratsiyalashganda almashtirish usuli yordamga keladi.

Misol.

Noaniq integralni toping .

Yechim.

Keling, yangi o'zgaruvchini kiritamiz. ifoda qilaylik X orqali z:

Olingan ifodalarni asl integralga almashtiramiz:

Antiderivativlar jadvalidan bizda .

Asl o'zgaruvchiga qaytish qoladi X:

Javob:

Funktsiya F(x ) chaqirdi antiderivativ funktsiya uchun f(x) ma'lum bir intervalda, agar hamma uchun x bu oraliqdan boshlab tenglik amal qiladi

F"(x ) = f(x ) .

Masalan, funktsiya F(x) = x 2 f(x ) = 2X , chunki

F"(x) = (x 2 )" = 2x = f(x). ◄

Antiderivativning asosiy xossasi

Agar F(x) - funksiyaning anti hosilasi f(x) berilgan oraliqda, keyin funksiya f(x) cheksiz ko'p antiderivativlarga ega va bu barcha antiderivativlarni ko'rinishda yozish mumkin F(x) + C, Qayerda BILAN ixtiyoriy doimiydir.

Masalan.

Funktsiya F(x) = x 2 + 1 funksiyaning antiderivatividir

f(x ) = 2X , chunki F"(x) = (x 2 + 1 )" = 2 x = f(x);

funktsiyasi F(x) = x 2 - 1 funksiyaning antiderivatividir

f(x ) = 2X , chunki F"(x) = (x 2 - 1)" = 2x = f(x) ;

funktsiyasi F(x) = x 2 - 3 funksiyaning antiderivatividir

f(x) = 2X , chunki F"(x) = (x 2 - 3)" = 2 x = f(x);

har qanday funktsiya F(x) = x 2 + BILAN , Qayerda BILAN - ixtiyoriy konstanta va faqat shunday funksiya funksiyaning anti hosilasi hisoblanadi f(x) = 2X . ◄

Antiderivativlarni hisoblash qoidalari

Agar F(x) - uchun antiderivativ f(x) , A G(x) - uchun antiderivativ g(x) , Bu F(x) + G(x) - uchun antiderivativ f(x) + g(x) . Boshqa so'zlar bilan aytganda, yig'indining antiderivativi antiderivativlar yig'indisiga teng .
Agar F(x) - uchun antiderivativ f(x) , Va k - doimiy, keyin k · F(x) - uchun antiderivativ k · f(x) . Boshqa so'zlar bilan aytganda, doimiy koeffitsient hosila belgisidan chiqarilishi mumkin .
Agar F(x) - uchun antiderivativ f(x) , Va k,b- doimiy va k ≠ 0 , Bu 1 / k F( k x+ b ) - uchun antiderivativ f(k x+ b) .

Noaniq integral

Noaniq integral funktsiyasidan f(x) ifoda deyiladi F(x) + C, ya'ni berilgan funksiyaning barcha anti hosilalari to'plami f(x) . Noaniq integral quyidagicha ifodalanadi:

∫ f(x) dx = F(x) + C ,

f(x)- chaqirishadi integral funktsiyasi ;

f(x) dx- chaqirishadi integral ;

x - chaqirishadi integratsiya o'zgaruvchisi ;

F(x) - ibtidoiy funktsiyalardan biri f(x) ;

BILAN ixtiyoriy doimiydir.

Masalan, ∫ 2 x dx =X 2 + BILAN , ∫ cosx dx = gunoh X + BILAN va hokazo. ◄

"Integral" so'zi lotincha so'zdan olingan butun son , bu "qayta tiklangan" degan ma'noni anglatadi. ning noaniq integralini hisobga olgan holda 2 x, biz funktsiyani tiklaganga o'xshaymiz X 2 ga teng bo'lgan hosilasi 2 x. Funksiyani hosilasidan tiklash yoki bir xil bo‘lsa, berilgan integralda noaniq integral topish deyiladi. integratsiya bu funksiya. Integratsiya - bu differensiallashning teskari operatsiyasi, integrasiyaning to'g'ri bajarilganligini tekshirish uchun natijani differentsiallash va integralni olish kifoya.

Noaniq integralning asosiy xossalari

Noaniq integralning hosilasi integralga teng:

(∫ f(x) dx )" = f(x) .

Integralning doimiy omili integral belgisidan chiqarilishi mumkin:

∫ k · f(x) dx = k · ∫ f(x) dx .

Funktsiyalar yig'indisining (farqining) integrali ushbu funktsiyalarning integrallari yig'indisiga (farqiga) teng:

∫ ( f(x) ± g(x ) ) dx = ∫ f(x) dx ± ∫ g (x ) dx .

Agar k,b- doimiy va k ≠ 0 , Bu

∫ f ( k x+ b) dx = 1 / k F( k x+ b ) + C .

Antiderivativlar va noaniq integrallar jadvali

	f(x)	F(x) + C	∫ f(x) dx = F(x) + C
I.	$$0$$	$$C$$	$$\int 0dx=C$$
II.	$$k$$	$$kx+C$$	$$\int kdx=kx+C$$
III.	$$x^n~(n\neq-1)$$	$$\frac(x^(n+1))(n+1)+C$$	$$\int x^ndx=\frac(x^(n+1))(n+1)+C$$
IV.	$$\frac(1)(x)$$	$$\ln \|x\|+C$$	$$\int\frac(dx)(x)=\ln \|x\|+C$$
V.	$$\sin x$$	$$-\cos x+C$$	$$\int\sin x~dx=-\cos x+C$$
VI.	$$\cos x$$	$$\sin x+C$$	$$\int\cos x~dx=\sin x+C$$
VII.	$$\frac(1)(\cos^2x)$$	$$\textrm(tg) ~x+C$$	$$\int\frac(dx)(\cos^2x)=\textrm(tg) ~x+C$$
VIII.	$$\frac(1)(\sin^2x)$$	$$-\textrm(ctg) ~x+C$$	$$\int\frac(dx)(\sin^2x)=-\textrm(ctg) ~x+C$$
IX.	$$e^x$$	$$e^x+C$$	$$\int e^xdx=e^x+C$$
X.	$$a^x$$	$$\frac(a^x)(\ln a)+C$$	$$\int a^xdx=\frac(a^x)(\ln a)+C$$
XI.	$$\frac(1)(\sqrt(1-x^2))$$	$$\arcsin x +C$$	$$\int\frac(dx)(\sqrt(1-x^2))=\arcsin x +C$$
XII.	$$\frac(1)(\sqrt(a^2-x^2))$$	$$\arcsin \frac(x)(a)+C$$	$$\int\frac(dx)(\sqrt(a^2-x^2))=\arcsin \frac(x)(a)+C$$
XIII.	$$\frac(1)(1+x^2)$$	$$\textrm(arctg) ~x+C$$	$$\int \frac(dx)(1+x^2)=\textrm(arctg) ~x+C$$
XIV.	$$\frac(1)(a^2+x^2)$$	$$\frac(1)(a)\textrm(arctg) ~\frac(x)(a)+C$$	$$\int \frac(dx)(a^2+x^2)=\frac(1)(a)\textrm(arctg) ~\frac(x)(a)+C$$
XV.	$$\frac(1)(\sqrt(a^2+x^2))$$	$$\ln\|x+\sqrt(a^2+x^2)\|+C$$	$$\int\frac(dx)(\sqrt(a^2+x^2))=\ln\|x+\sqrt(a^2+x^2)\|+C$$
XVI.	$$\frac(1)(x^2-a^2)~(a\neq0)$$	$$\frac(1)(2a)\ln \begin(vmatrix)\frac(x-a)(x+a)\end(vmatrix)+C$$	$$\int\frac(dx)(x^2-a^2)=\frac(1)(2a)\ln \begin(vmatrix)\frac(x-a)(x+a)\end(vmatrix)+ C$$
XVII.	$$\textrm(tg) ~x$$	$$-\ln \|\cos x\|+C$$	$$\int \textrm(tg) ~x ~dx=-\ln \|\cos x\|+C$$
XVIII.	$$\textrm(ctg) ~x$$	$$\ln \|\sin x\|+C$$	$$\int \textrm(ctg) ~x ~dx=\ln \|\sin x\|+C$$
XIX.	$$ \frac(1)(\sin x) $$	$$\ln \begin(vmatrix)\textrm(tg) ~\frac(x)(2)\end(vmatrix)+C $$	$$\int \frac(dx)(\sin x)=\ln \begin(vmatrix)\textrm(tg) ~\frac(x)(2)\end(vmatrix)+C $$
XX.	$$ \frac(1)(\cos x) $$	$$\ln \begin(vmatrix)\textrm(tg)\chap (\frac(x)(2)+\frac(\pi )(4) \o'ng) \end(vmatrix)+C $$	$$\int \frac(dx)(\cos x)=\ln \begin(vmatrix)\textrm(tg)\chap (\frac(x)(2)+\frac(\pi )(4) \o'ng ) \end(vmatrix)+C $$
Ushbu jadvalda berilgan antiderivativ va noaniq integrallar odatda deyiladi jadvalli antiderivativlar Va jadval integrallari .

Aniq integral

O'rtaga qo'ying [a; b] uzluksiz funksiya berilgan y = f(x) , Keyin a dan b gacha bo'lgan aniq integral funktsiyalari f(x) antiderivativning ortishi deyiladi F(x) bu funktsiya, ya'ni

$$\int_(a)^(b)f(x)dx=F(x)|(_a^b) = ~~F(a)-F(b).$$

Raqamlar a Va b mos ravishda chaqiriladi pastroq Va yuqori integratsiya chegaralari.

Aniq integralni hisoblashning asosiy qoidalari

1. $\int_(a)^(a)f(x)dx=0$;

2. $\int_(a)^(b)f(x)dx=- \int_(b)^(a)f(x)dx$;

3. $\int_(a)^(b)kf(x)dx=k\int_(a)^(b)f(x)dx,$ bu yerda k - doimiy;

4. $\int_(a)^(b)(f(x) ± g(x))dx=\int_(a)^(b)f(x) dx±\int_(a)^(b) g(x)dx$;

5. $\int_(a)^(b)f(x)dx=\int_(a)^(c)f(x)dx+\int_(c)^(b)f(x)dx$;

6. $\int_(-a)^(a)f(x)dx=2\int_(0)^(a)f(x)dx$, bu yerda f(x) — teng funksiya;

7. $\int_(-a)^(a)f(x)dx=0$, bu yerda f(x) g'alati funktsiyadir.

Izoh . Barcha hollarda integrallar sonli intervallarda integrallash mumkin deb hisoblanadi, ularning chegaralari integrallash chegarasi hisoblanadi.

Aniq integralning geometrik va fizik ma'nosi

Geometrik ma'no aniq integral	Jismoniy ma'no aniq integral

Kvadrat S egri chiziqli trapezoid (oraliqdagi uzluksiz musbat grafigi bilan chegaralangan raqam [a; b] funktsiyalari f(x) , eksa ho'kiz va tekis x=a , x=b ) formula bo'yicha hisoblanadi $$S=\int_(a)^(b)f(x)dx.$$	Yo'l s, moddiy nuqta yengib o'tgan, qonunga muvofiq o'zgaruvchan tezlik bilan to'g'ri chiziqli harakat v(t) , bir muddat a ; b] , keyin ushbu funktsiyalar va to'g'ri chiziqlar grafiklari bilan chegaralangan shaklning maydoni x = a , x = b , formula bo'yicha hisoblanadi $$S=\int_(a)^(b)(f(x)-g(x))dx.$$
	Masalan. Chiziqlar bilan chegaralangan shaklning maydonini hisoblaylik y = x 2 Va y= 2- x . Keling, ushbu funktsiyalarning grafiklarini sxematik tarzda tasvirlaymiz va maydonini topish kerak bo'lgan rasmni boshqa rangda ajratib ko'rsatamiz. Integratsiya chegaralarini topish uchun tenglamani yechamiz: x 2 = 2- x ; x 2 + x- 2 = 0 ; x 1 = -2, x 2 = 1 . $$S=\int_(-2)^(1)((2-x)-x^2)dx=$$
$$=\int_(-2)^(1)(2-x-x^2)dx=\chap (2x-\frac(x^2)(2)-\frac(x^3)(2) \oʻng )\bigm\|(_(-2)^(~1))=4\frac(1)(2). $$ ◄

Aylanish jismining hajmi

Agar tana o'q atrofida aylanish natijasida olingan bo'lsa ho'kiz intervalda uzluksiz va manfiy bo'lmagan grafik bilan chegaralangan egri chiziqli trapezoid [a; b] funktsiyalari y = f(x) va tekis x = a Va x = b , keyin chaqiriladi aylanish tanasi .

Aylanish jismining hajmi formula bo'yicha hisoblanadi

$$V=\pi\int_(a)^(b)f^2(x)dx.$$

Agar inqilob tanasi yuqorida va pastda funktsiyalar grafiklari bilan chegaralangan figuraning aylanishi natijasida olingan bo'lsa. y = f(x) Va y = g(x) , mos ravishda, keyin

$$V=\pi\int_(a)^(b)(f^2(x)-g^2(x))dx.$$

Masalan. Radiusli konusning hajmini hisoblaymiz r va balandligi h .

Konusni to'rtburchaklar koordinatalar tizimida shunday joylashtiramizki, uning o'qi o'qiga to'g'ri keladi. ho'kiz , va asosning markazi boshlang'ich qismida joylashgan edi. Generatorning aylanishi AB konusni belgilaydi. Tenglamadan beri AB

$$\frac(x)(h)+\frac(y)(r)=1,$$

$$y=r-\frac(rx)(h)$$

va bizda bo'lgan konusning hajmi uchun

$$V=\pi\int_(0)^(h)(r-\frac(rx)(h))^2dx=\pi r^2\int_(0)^(h)(1-\frac( x)(h))^2dx=-\pi r^2h\cdot \frac((1-\frac(x)(h))^3)(3)|(_0^h)=-\pi r^ 2soat\chap (0-\frac(1)(3) \o'ng)=\frac(\pi r^2h)(3).$$

◄

Prototip. Chiroyli so'z.) Birinchidan, biroz ruscha. Bu so'z aynan shunday talaffuz qilinadi, emas "prototip" , tuyulishi mumkin. Antiderivativ barcha integral hisoblarning asosiy tushunchasidir. Har qanday integrallar - noaniq, aniq (siz ular bilan shu semestrda tanish bo'lasiz), shuningdek, qo'sh, uch, egri chiziqli, sirt (va bu allaqachon ikkinchi yilning asosiy belgilari) - bu asosiy tushunchaga asoslanadi. O'zlashtirish uchun to'liq ma'noga ega. Qani ketdik.)

Antiderivativ tushunchasi bilan tanishishdan oldin, keling, eng umumiy ma'noda eng keng tarqalganini eslaylik. hosila. Chegaralarning zerikarli nazariyasini, argumentlarning o'sishini va boshqa narsalarni o'rganmasdan, aytishimiz mumkinki, hosila topish (yoki farqlash) oddiygina matematik amaldir funktsiyasi. Ana xolos. Har qanday funktsiya olinadi (masalan, f(x) = x2) Va ma'lum qoidalarga muvofiq ga aylanadi yangi xususiyat. Va bu bitta yangi xususiyat va deyiladi hosila.

Bizning holatda, differentsiatsiyadan oldin funktsiya mavjud edi f(x) = x2, va farqlashdan keyin u allaqachon bo'ldi boshqa funktsiya f’(x) = 2x.

Hosil– chunki bizning yangi funksiyamiz f’(x) = 2x sodir bo'ldi funktsiyasidan f(x) = x2. Differensiatsiya operatsiyasi natijasida. Va, xususan, boshqa funktsiyadan emas, balki undan ( x 3, Masalan).

Qo'pol qilib aytganda, f(x) = x2- bu onam va f’(x) = 2x- uning sevimli qizi.) Bu tushunarli. Keling, davom etaylik.

Matematiklar tinchlanmaydigan odamlardir. Har bir harakat uchun ular reaktsiya topishga harakat qilishadi. :) Qo'shish bor - ayirish ham bor. Ko‘paytirish ham, bo‘lish ham bor. Qudratga ko'tarish - ildizni chiqarib tashlash. Sinus - arksinus. Aynan bir xil farqlash- bu bor degani... integratsiya.)

Endi qiziqarli muammoni qo'yaylik. Masalan, bizda shunday oddiy funksiya bor f(x) = 1. Va biz bu savolga javob berishimiz kerak:

WHAT funksiyasining hosilasi bizga funktsiyani beradif(x) = 1?

Boshqacha qilib aytganda, qizini ko'rib, DNK tahlilidan foydalanib, uning onasi kimligini aniqlang. :) Xo'sh, qaysi biri? original funksiya (uni F(x) deb ataymiz) bizning hosila f(x) = 1 funksiyasi? Yoki matematik shaklda, buning uchun F(x) funksiyasi quyidagi tenglikka ega:

F’(x) = f(x) = 1?

Elementar misol. Men harakat qildim.) Biz shunchaki F(x) funksiyasini tanlaymiz, shunda tenglik ishlaydi. :) Xo'sh, topdingizmi? Ha, albatta! F(x) = x. Chunki:

F’(x) = x’ = 1 = f(x).

Albatta, topilgan onam F(x) = x Men buni biror narsa deb atashim kerak, ha.) Men bilan tanishing!

Funktsiya uchun antiderivativf(x) shunday funksiya chaqiriladiF(x), hosilasi teng bo'lganf(x), ya'ni. ular uchun tenglik amal qiladiF’(x) = f(x).

Bo'ldi shu. Boshqa ilmiy fokuslar yo'q. Qattiq ta'rifda qo'shimcha ibora qo'shiladi "X oralig'ida". Ammo biz hozircha bu nozikliklarni o'rganmaymiz, chunki bizning asosiy vazifamiz - bu ibtidoiy narsalarni topishni o'rganish.

Bizning holatda, bu funktsiyaga aylanadi F(x) = x hisoblanadi antiderivativ funktsiya uchun f(x) = 1.

Nega? Chunki F’(x) = f(x) = 1. x ning hosilasi bitta. E'tirozlar yo'q.)

"Prototip" atamasi umumiy tilda "ajdod", "ota-ona", "ajdod" degan ma'noni anglatadi. Biz darhol eng yaqin va aziz odamni eslaymiz.) Va antiderivativni qidirishning o'zi asl funktsiyani tiklashdir. ma'lum hosilasi bilan. Boshqacha aytganda, bu harakat farqlashning teskarisi. Ana xolos! Ushbu ajoyib jarayonning o'zi ham ilmiy jihatdan deyiladi - integratsiya. Lekin haqida integrallar- Keyinroq. Sabr, do'stlar!)

Eslab qoling:

Integratsiya - bu funksiya ustidagi matematik operatsiya (masalan, differentsiatsiya).

Integratsiya - bu differentsiatsiyaning teskari operatsiyasi.

Antiderivativ integratsiya natijasidir.

Endi vazifani murakkablashtiramiz. Endi funksiya uchun antiderivativ topamiz f(x) = x. Ya'ni, biz topamiz bunday funktsiya F(x) , uchun uning hosilasi X ga teng bo'ladi:

F'(x) = x

Sanoat bilan tanish bo'lgan har bir kishi, ehtimol, shunday bir narsa xayoliga keladi:

(x 2)’ = 2x.

Xo'sh, hosilalar jadvalini eslaganlarga hurmat va hurmat!) To'g'ri. Lekin bitta muammo bor. Bizning asl funktsiyamiz f(x) = x, A (x 2)’ = 2 x. Ikki X. Va farqlashdan keyin biz olishimiz kerak faqat x. Aylanmaydi. Lekin…

Siz va men ilmli xalqmiz. Biz sertifikatlarimizni oldik.) Va maktabdan bilamizki, har qanday tenglikning ikkala tomoni ham bir xil songa ko'paytirilishi va bo'linishi mumkin (albatta, noldan tashqari)! Bo'ldi shu tartibga solingan. Keling, bu imkoniyatni o'z manfaatimiz uchun ishlataylik.)

Biz sof X o'ng tomonda qolishini xohlaymiz, to'g'rimi? Lekin ikkalasi yo'lni to'sib qo'yadi... Shunday qilib, hosila (x 2)’ = 2x uchun nisbatni olamiz va bo'linadi. uning ikkala qismi bu ikkitasiga:

Shunday qilib, bir narsa allaqachon aniq bo'lib bormoqda. Keling, davom etaylik. Biz bilamizki, har qanday doimiy bo'lishi mumkin belgisidan hosilani oling. Shunga o'xshash:

Matematikadagi barcha formulalar chapdan o'ngga va aksincha - o'ngdan chapga ishlaydi. Bu shuni anglatadiki, bir xil muvaffaqiyat bilan har qanday doimiy bo'lishi mumkin hosila belgisi ostiga kiriting:

Bizning holatda, biz ikkalasini hosila belgisi ostida maxrajda (yoki bir xil narsa, koeffitsient 1/2) yashiramiz:

Va hozir diqqat bilan Keling, yozuvimizni batafsil ko'rib chiqaylik. Biz nimani ko'ramiz? ning hosilasi ekanligini bildiruvchi tenglikni ko'ramiz nimadir(Bu nimadir- qavs ichida) X ga teng.

Olingan tenglik faqat funktsiya uchun kerakli antiderivativ degan ma'noni anglatadi f(x) = x vazifasini bajaradi F(x) = x 2 /2 . Qo'shtirnoq ostidagi qavs ichida. To'g'ridan-to'g'ri antiderivativ ma'nosida.) Xo'sh, natijani tekshiramiz. Keling, hosilani topamiz:

Ajoyib! Asl funktsiya olinadi f(x) = x. Ular raqsga tushgan narsadan qaytib kelishdi. Bu bizning antiderivativimiz to'g'ri topilganligini anglatadi.)

Agar .. bo'lsa nima bo'ladi f(x) = x2? Uning antiderivativi nimaga teng? Savol yo'q! Siz va men bilamiz (yana farqlash qoidalaridan):

3x 2 = (x 3)’

VA, shuning uchun,

Tushundim? Endi biz o'zimiz uchun sezilmaydigan tarzda har qanday uchun antiderivativlarni hisoblashni o'rgandik quvvat funksiyasi f(x)=x n. Ongda.) Dastlabki ko'rsatkichni oling n, uni bittaga oshiring va kompensatsiya sifatida butun tuzilmani bo'ling n+1:

Olingan formula, aytmoqchi, to'g'ri nafaqat tabiiy ko'rsatkich uchun daraja n, balki boshqa har qanday uchun ham - salbiy, kasr. Bu oddiylardan antiderivativlarni topishni osonlashtiradi kasrlar Va ildizlar.

Masalan:

Tabiiyki, n ≠ -1 , aks holda formulaning maxraji nolga aylanadi va formula o'z ma'nosini yo'qotadi.) Ushbu maxsus holat haqida n = -1 birozdan keyin.)

Noaniq integral nima? Integrallar jadvali.

Aytaylik, funksiyaning hosilasi nimaga teng F(x) = x? Xo'sh, bitta, bitta - norozi javoblarni eshitaman ... To'g'ri. Birlik. Lekin... Funktsiya uchun G(x) = x+1 hosila ham bittaga teng bo'ladi:

Shuningdek, hosila funktsiya uchun birlikka teng bo'ladi x+1234 , va funksiya uchun x-10 , va shaklning boshqa har qanday funksiyasi uchun x+C , Qayerda BILAN - har qanday doimiy. Chunki har qanday doimiyning hosilasi nolga teng va nolni qoʻshish/ayirish hech kimni sovuq yoki issiq his qilmaydi.)

Bu noaniqlikka olib keladi. Ma'lum bo'lishicha, funktsiya uchun f(x) = 1 prototip sifatida xizmat qiladi shunchaki funktsiya emas F(x) = x , balki funksiya hamdir F 1 (x) = x+1234 va funksiya F 2 (x) = x-10 va hokazo!

Ha. Aynan shunday.) Har biri uchun ( intervalda uzluksiz) funktsiyaning faqat bitta antiderivativi emas, balki cheksiz ko'p - butun oila! Faqat bitta ona yoki dadam emas, balki butun oila daraxti, ha.)

Lekin! Bizning barcha ibtidoiy qarindoshlarimiz bitta muhim umumiy xususiyatga ega. Shuning uchun ular qarindoshlardir.) Mulk shunchalik muhimki, integratsiya usullarini tahlil qilish jarayonida biz uni bir necha marta eslaymiz. Va biz buni uzoq vaqt eslaymiz.)

Mana, bu mulk:

Har qanday ikkita antiderivativ F 1 (x) VaF 2 (x) xuddi shu funksiyadanf(x) doimiy bilan farqlanadi:

F 1 (x) - F 2 (x) = S.

Agar kimdir dalilga qiziqsa, adabiyot yoki ma'ruza matnlarini o'rganing.) Mayli, shunday bo'lsin, men buni isbotlayman. Yaxshiyamki, bu erda isbot elementar, bir qadamda. Keling, tenglikni olaylik

F 1 (x) - F 2 (x) = C

Va Keling, uning ikkala qismini farqlaylik. Ya'ni, biz shunchaki ahmoqona zarbalarni qo'shamiz:

Bo'ldi shu. Ular aytganidek, CHT. :)

Bu mulk nimani anglatadi? Va ikki xil antiderivativlar haqida bir xil funktsiyadan f(x) bilan farq qila olmaydi X bilan qandaydir ifoda . Faqat qat'iy ravishda doimiy ravishda! Boshqacha qilib aytganda, agar bizda qandaydir jadval mavjud bo'lsa asl nusxalardan biri(F(x) bo'lsin), keyin grafiklar boshqalar Bizning antiderivativlarimiz F(x) grafigini y o'qi bo'ylab parallel o'tkazish yo'li bilan tuzilgan.

Keling, misol funksiyasidan foydalangan holda qanday ko'rinishini ko'rib chiqaylik f(x) = x. Uning barcha ibtidoiylari, biz allaqachon bilganimizdek, umumiy shaklga ega F(x) = x 2 /2+C . Rasmda shunday ko'rinadi cheksiz sonli parabolalar, “asosiy” paraboladan y = x 2 /2 konstanta qiymatiga qarab OY o'qi bo'ylab yuqoriga yoki pastga siljish orqali olingan. BILAN.

Funktsiyaning maktab grafigini eslang y=f(x)+a jadval almashinuvi y=f(x) Y o'qi bo'ylab "a" birliklari bilanmi?) Bu erda ham xuddi shunday.)

Bundan tashqari, e'tibor bering: bizning parabolalarimiz hech bir joyda kesishmang! Bu tabiiy. Axir, ikki xil funksiya y 1 (x) va y 2 (x) muqarrar ravishda mos keladi. doimiyning ikki xil qiymati – C 1 Va C 2.

Demak, y 1 (x) = y 2 (x) tenglama hech qachon yechimga ega emas:

C 1 = C 2

x ∊ ∅ , chunki C 1 ≠ C2

Va endi biz asta-sekin integral hisobning ikkinchi asosiy kontseptsiyasiga yaqinlashmoqdamiz. Hozirgina aniqlaganimizdek, har qanday f(x) funksiya uchun bir-biridan doimiy qiymat bilan farq qiluvchi cheksiz F(x) + C anti hosilalar to‘plami mavjud. Bu eng cheksiz to'plamning ham o'ziga xos nomi bor.) Iltimos, seving va iltifot qiling!

Noaniq integral nima?

Funktsiya uchun barcha antiderivativlar to'plami f(x) deyiladi noaniq integral funktsiyasidanf(x).

Bu butun ta'rif.)

"Noaniq" - chunki bir xil funktsiya uchun barcha antiderivativlar to'plami cheksiz. Juda ko'p turli xil variantlar.)

"Integral" - biz ushbu shafqatsiz so'zning batafsil dekodlanishi bilan keyingi katta bo'limda tanishamiz. aniq integrallar. Hozircha, taxminiy shaklda, biz bir narsani integral sifatida ko'rib chiqamiz umumiy, birlashgan, yaxlit. Va integratsiya orqali - uyushma, umumlashtirish, bu holda, xususiy (hosil) dan umumiy (antiderivativ) ga o'tish. Shunga o'xshash narsa.

Noaniq integral quyidagicha ifodalanadi:

U qanday yozilgan bo'lsa, xuddi shunday o'qiydi: x de x dan integral ef. Yoki integral dan ef dan x de x. Xo'sh, tushunasiz.)

Endi belgini ko'rib chiqaylik.

∫ - integral belgisi. Ma'nosi hosila uchun bosh harf bilan bir xil.)

d - belgisidifferensial. Qo'rqmaylik! Nima uchun bu kerakligi biroz pastroq.

f(x) - integral("s" orqali).

f(x)dx - integral ifodasi. Yoki, taxminan, integralni "to'ldirish".

Noaniq integral ma'nosiga ko'ra,

Bu yerga F(x)- xuddi shunday antiderivativ funktsiya uchun f(x) biz qandaydir tarzda o'zimiz topdik. Ular buni qanday aniq topdilar, bu gap emas. Masalan, biz buni topdik F(x) = x 2 /2 uchun f(x)=x.

"BILAN" - ixtiyoriy doimiy. Yoki ko'proq ilmiy, integral doimiy. Yoki integratsiya konstantasi. Hammasi bitta.)

Endi antiderivativni topishning birinchi misollarimizga qaytaylik. Noaniq integral nuqtai nazaridan, endi ishonch bilan yozishimiz mumkin:

Integral konstanta nima va u nima uchun kerak?

Savol juda qiziq. Va juda (JUDA!) Muhim. Butun cheksiz antiderivativlar to'plamidan integral doimiy chiziqni ajratib turadi qaysi ma'lum bir nuqtadan o'tadi.

Buning nima keragi bor? Antiderivativlarning dastlabki cheksiz to'plamidan (ya'ni. noaniq integral) berilgan nuqtadan o'tadigan egri chiziqni tanlashingiz kerak. Ba'zilar bilan maxsus koordinatalar. Bunday vazifa har doim va hamma joyda integrallar bilan dastlabki tanishish paytida yuzaga keladi. Maktabda ham, universitetda ham.

Oddiy muammo:

f=x funksiyaning barcha anti hosilalari to‘plamidan (2;2) nuqtadan o‘tuvchisini tanlang.

Biz boshimiz bilan o'ylashni boshlaymiz ... Barcha ibtidoiylarning to'plami birinchi navbatda biz kerak degan ma'noni anglatadi asl funktsiyamizni birlashtiring. Ya'ni, x(x). Biz buni biroz yuqoriroq qildik va quyidagi javobni oldik:

Endi bizda nima borligini aniqlaymiz. Bizda faqat bitta funktsiya emas, balki funktsiyalarning butun oilasi. Qaysi biri aniq? Vida y=x 2 /2+C . C doimiysi qiymatiga bog'liq. Va biz endi "tutib olishimiz" kerak bo'lgan doimiyning mana shu qiymati.) Xo'sh, ushlay boshlaylik?)

Bizning qarmoq - egri chiziqlar oilasi (parabolalar) y=x 2 /2+C.

Konstantalar - bu baliqlar. Ko'p va ko'p. Ammo har birining o'z ilgagi va o'ljasi bor.)

O'lja nima? To'g'ri! Bizning nuqtamiz (-2;2).

Shunday qilib, biz nuqtamizning koordinatalarini antiderivativlarning umumiy shakliga almashtiramiz! Biz olamiz:

y(2) = 2

Bu yerdan topish oson C=0.

Bu qanday ma'nono bildiradi? Bu shaklning barcha cheksiz parabola to'plamidan degan ma'noni anglatadiy=x 2 /2+Cfaqat doimiy C=0 bo'lgan parabola bizga yarashadi! Ya'ni:y=x 2 /2. Va faqat u. Bizga kerakli nuqtadan faqat shu parabola o'tadi (-2; 2). Va ichidabizning oilamizdagi barcha boshqa parabolalar o'tadi bu nuqta ular endi bo'lmaydi. Samolyotning boshqa ba'zi nuqtalari orqali - ha, lekin (2; 2) nuqta orqali - endi yo'q. Tushundim?

Aniqlik uchun bu erda ikkita rasm - parabolalarning butun oilasi (ya'ni noaniq integral) va ba'zilari maxsus parabola, mos keladi doimiyning o'ziga xos qiymati va orqali o'tish aniq nuqta:

Doimiylikni hisobga olish qanchalik muhimligini ko'rasiz BILAN integratsiyada! Shuning uchun bu "C" harfini e'tiborsiz qoldirmang va uni yakuniy javobga qo'shishni unutmang.

Keling, nima uchun bu belgi integrallarning hamma joyida osilganligini aniqlaylik dx . Talabalar buni ko'pincha unutishadi... Darvoqe, bu ham xato! Va juda qo'pol. Gap shundaki, integratsiya differentsiatsiyaning teskari amalidir. Va aniq nima farqlash natijasi? Hosilmi? To'g'ri, lekin butunlay emas. Differensial!

Bizning holatda, funktsiya uchun f(x) uning antiderivativining differensialligi F(x), qiladi:

Ushbu zanjirni tushunmaydiganlar uchun zudlik bilan differentsialning ta'rifi va ma'nosini va u qanchalik aniq ochilganini takrorlang! Aks holda, siz integrallarda shafqatsizlarcha sekinlashasiz...

Sizga shuni eslatib o'tamanki, eng qo'pol ko'rinishda, har qanday f(x) funksiyaning differensialligi shunchaki hosiladir. f'(x)dx. Ana xolos! Hosilini oling va uni ko'paytiring differensial argumentga(masalan, dx). Ya'ni, har qanday differentsial, mohiyatiga ko'ra, odatiy hisoblash uchun tushadi hosila.

Shuning uchun, qat'iy aytganda, integral "olinmaydi" funktsiyalari f(x), odatda ishonganidek va dan differensial f(x)dx! Ammo, soddalashtirilgan versiyada buni aytish odatiy holdir "integral funktsiyadan olingan". Yoki: "f funktsiyasi integrallashgan(x)". Xuddi shu narsa. Va biz xuddi shunday gapiramiz. Ammo nishon haqida dx Unutmaylik! :)

Va endi men sizga yozish paytida buni qanday unutmaslik kerakligini aytaman. Avval siz x o'zgaruvchisiga nisbatan oddiy hosilani hisoblayotganingizni tasavvur qiling. Odatda qanday yozasiz?

Bu kabi: f’(x), y’(x), y’ x. Yoki aniqroq, differentsial nisbat orqali: dy/dx. Bu yozuvlarning barchasi hosila X ga nisbatan aniq olinganligini ko'rsatadi. Va "igrek", "te" yoki boshqa o'zgaruvchilar bilan emas.)

Xuddi shu narsa integrallarga ham tegishli. Yozib olish ∫ f(x)dx biz ham go'yo integratsiyaning aniq amalga oshirilganligini ko'rsatadi x o'zgaruvchisi bo'yicha. Albatta, bularning barchasi juda soddalashtirilgan va qo'pol, ammo tushunarli, umid qilamanki. Va imkoniyatlar unut hamma joyda mavjudlik xususiyati dx keskin pasayish.)

Shunday qilib, biz noaniq integral nima ekanligini aniqladik. Ajoyib.) Endi mana shu noaniq integrallarni o'rganish yaxshi bo'lardi hisoblash. Yoki oddiy qilib aytganda, "oling". :) Va bu erda talabalarni ikkita yangilik kutmoqda - yaxshi va unchalik yaxshi emas. Hozircha yaxshisidan boshlaylik.)

Yangilik yaxshi. Integrallar uchun ham, hosilalar uchun ham o'ziga xos jadval mavjud. Va biz yo'lda duch keladigan barcha integrallarni, hatto eng dahshatli va murakkablarini ham ma'lum qoidalarga muvofiq Qanday bo'lmasin, biz buni jadvalli jadvallarga qisqartiramiz.)

Demak, u shu yerda integrallar jadvali!

Mana, eng mashhur funksiyalardan integrallarning shunday chiroyli jadvali. 1-2 formulalar guruhiga (doimiy va quvvat funktsiyasi) alohida e'tibor berishni tavsiya etaman. Bu integrallarda eng ko'p ishlatiladigan formulalar!

Formulalarning uchinchi guruhi (trigonometriya), siz taxmin qilganingizdek, hosilalar uchun mos keladigan formulalarni oddiygina teskari aylantirish orqali olinadi.

Masalan:

To'rtinchi formulalar guruhi (eksponensial funktsiya) bilan hamma narsa o'xshash.

Va bu erda biz uchun formulalarning oxirgi to'rtta guruhi (5-8). yangi. Ular qaerdan paydo bo'lgan va bu ekzotik funktsiyalar to'satdan asosiy integrallar jadvaliga kirdi? Nima uchun bu funktsiyalar guruhlari boshqa funktsiyalardan ajralib turadi?

Rivojlanish jarayonida tarixan shunday bo'lgan integratsiya usullari . Biz eng xilma-xil integrallarni olishni mashq qilsak, jadvalda keltirilgan funktsiyalarning integrallari juda tez-tez sodir bo'lishini tushunasiz. Ko'pincha matematiklar ularni jadvalli integrallar deb tasniflashgan.) Ular orqali murakkab tuzilmalardan boshqa ko'plab integrallar ifodalanadi.

Faqat o'yin-kulgi uchun siz ushbu dahshatli formulalardan birini olishingiz va uni farqlashingiz mumkin. :) Masalan, eng shafqatsiz 7-formula.

Hammasi yaxshi. Matematiklar aldanib qolishmadi. :)

Integrallar jadvalini, shuningdek hosilalar jadvalini yoddan bilish maqsadga muvofiqdir. Har holda, formulalarning dastlabki to'rtta guruhi. Bu birinchi qarashda ko'rinadigan darajada qiyin emas. Oxirgi to'rtta guruhni yodlang (kasrlar va ildizlar bilan) Xayr bunga loyiq emas. Baribir, avvaliga logarifmni qayerga yozishni, arktangent qayerda, arksinus qayerda, qayerda 1/a, qayerda 1/2a... Birgina chiqish yo‘li bor – ko‘proq misollar yeching. Keyin stol asta-sekin o'z-o'zidan eslab qoladi va shubhalar kemirishni to'xtatadi.)

Jadvalga diqqat bilan qaraydigan qiziquvchan odamlar savol berishlari mumkin: boshqa boshlang'ich "maktab" funktsiyalarining integrallari jadvalning qayerida - tangens, logarifm, "yoylar"? Aytaylik, nima uchun jadvalda sinusdan integral bor, lekin tangensdan integral YO'Q. tg x? Yoki logarifmning integrali yo'q ln x? Arksinusdan arcsin x? Nega ular yomonroq? Ammo u ba'zi "chap qo'l" funktsiyalariga to'la - ildizlar, kasrlar, kvadratlar bilan ...

Javob. Bundan ham yomoni yo'q.) Faqat yuqoridagi integrallar (tangens, logarifm, arksinus va boshqalardan) jadvalli emas . Va ular amalda jadvalda keltirilganlarga qaraganda kamroq uchraydi. Shuning uchun, biling yurakdan, ular teng bo'lgan narsa umuman kerak emas. Faqat bilish kifoya ular qanday hisoblab chiqiladi.)

Nima, kimdir hali ham chiday olmayaptimi? Shunday bo'lsin, ayniqsa siz uchun!

Xo'sh, uni yodlab olmoqchimisiz? :) Yo'qmi? Va qilmang.) Lekin tashvishlanmang, biz bunday integrallarning barchasini albatta topamiz. Tegishli darslarda. :)

Xo'sh, endi noaniq integralning xossalariga o'tamiz. Ha, ha, hech narsa qilib bo'lmaydi! Yangi kontseptsiya kiritiladi va uning ba'zi xususiyatlari darhol ko'rib chiqiladi.

Noaniq integralning xossalari.

Endi unchalik yaxshi xabar emas.

Farqlashdan farqli o'laroq, integratsiyaning umumiy standart qoidalari, adolatli barcha holatlar uchun, matematikada emas. Bu ajoyib!

Misol uchun, barchangiz buni juda yaxshi bilasiz (umid qilamanki!). har qanday ish har qanday Ikki funktsiya f(x) g(x) quyidagicha differensiallanadi:

(f(x) g(x))’ = f’(x) g(x) + f(x) g’(x).

Har qanday ko'rsatkich quyidagicha farqlanadi:

Va har qanday murakkab funktsiya, qanchalik murakkab bo'lmasin, quyidagicha farqlanadi:

Va f va g harflari ostida qanday funktsiyalar yashiringan bo'lishidan qat'i nazar, umumiy qoidalar hali ham ishlaydi va hosila, u yoki bu tarzda topiladi.

Ammo integrallar bilan bunday raqam endi ishlamaydi: mahsulot, qism (kasr), shuningdek, umumiy integratsiya formulalarining murakkab funktsiyasi uchun mavjud emas! Hech qanday standart qoidalar yo'q! To'g'rirog'i, ular mavjud. Men matematikani behuda xafa qildim.) Lekin, birinchidan, ular farqlashning umumiy qoidalariga qaraganda ancha kam. Ikkinchidan, biz keyingi darslarda gaplashadigan integratsiya usullarining aksariyati juda aniq. Va ular faqat ma'lum, juda cheklangan funktsiyalar sinfi uchun amal qiladi. Aytaylik, faqat uchun kasrli ratsional funksiyalar. Yoki boshqalar.

Va ba'zi integrallar, garchi ular tabiatda mavjud bo'lsa ham, boshlang'ich "maktab" funktsiyalari orqali umuman ifodalanmaydi! Ha, ha, va bunday integrallar juda ko'p! :)

Shuning uchun integratsiya farqlashdan ko'ra ko'proq vaqt va mashaqqatli ishdir. Lekin buning ham o'ziga xos jihati bor. Ushbu faoliyat ijodiy va juda hayajonli.) Va agar siz integrallar jadvalini yaxshi tushunsangiz va kamida ikkita asosiy texnikani o'zlashtirsangiz, ular haqida keyinroq gaplashamiz ( va ), unda sizga integratsiya juda yoqadi. :)

Endi noaniq integralning xossalari bilan tanishamiz. Ular umuman yo'q. Mana ular.

Birinchi ikkita xususiyat hosilalar uchun bir xil xususiyatlarga to'liq o'xshash va deyiladi noaniq integralning chiziqlilik xossalari . Bu yerda hamma narsa sodda va mantiqiy: yig‘indining/farqning integrali integrallarning yig‘indisi/farqiga teng, doimiy omil esa integral belgisidan chiqarilishi mumkin.

Ammo keyingi uchta xususiyat biz uchun tubdan yangi. Keling, ularni batafsil ko'rib chiqaylik. Ular rus tilida quyidagicha yangraydi.

Uchinchi mulk

Integralning hosilasi integralga teng

Hamma narsa oddiy, xuddi ertakdagi kabi. Agar siz funktsiyani integrallab, natijaning hosilasini topsangiz, unda... asl integratsiya funksiyasini olasiz. :) Bu xususiyat har doim (va kerak) integratsiyaning yakuniy natijasini tekshirish uchun ishlatilishi mumkin. Siz integralni hisobladingiz - javobni farqlang! Biz integral funktsiyasini oldik - OK. Agar biz uni olmagan bo'lsak, demak, biz biror joyda aralashib qoldik. Xatoni qidiring.)

Albatta, javob shu qadar shafqatsiz va mashaqqatli funktsiyalarga olib kelishi mumkinki, ularni farqlash istagi yo'q, ha. Ammo iloji bo'lsa, o'zingizni tekshirishga harakat qilish yaxshiroqdir. Hech bo'lmaganda bu oson bo'lgan misollarda.)

To'rtinchi mulk

Integralning differensialligi integralga teng .

Bu erda hech qanday maxsus narsa yo'q. Mohiyat bir xil, oxirida faqat dx paydo bo'ladi. Oldingi mulk va differentsial ochish qoidalariga ko'ra.

Beshinchi mulk

Ayrim funksiya differensialining integrali bu funksiya va ixtiyoriy doimiyning yig‘indisiga teng. .

Bu ham juda oddiy xususiyatdir. Bundan integrallarni yechish jarayonida ham muntazam foydalanamiz. Ayniqsa - ichida va.

Bu foydali xususiyatlar. Men sizni bu erda ularning qat'iy dalillari bilan zeriktirmoqchi emasman. Men buni qilishni xohlaydiganlarga buni o'zlari qilishlarini maslahat beraman. To'g'ridan-to'g'ri hosila va differentsial ma'noda. Men faqat oxirgi, beshinchi xususiyatni isbotlayman, chunki u kamroq aniq.

Shunday qilib, bizda bayonot bor:

Biz integralimizning "to'ldirilishi" ni olib tashlaymiz va uni differentsial ta'rifiga ko'ra ochamiz:

Har holda, shuni eslatib o'tamanki, hosila va antiderivativ belgilarimizga ko'ra, F’(x) = f(x) .

Endi biz natijamizni integral ichiga kiritamiz:

Aniq qabul qilingan noaniq integralning ta'rifi (rus tili meni kechirsin)! :)

Ana xolos.)

Xo'sh. Shu bilan integrallarning sirli olami bilan dastlabki tanishuvimizni tugallangan deb hisoblayman. Bugun men ishlarni yakunlashni taklif qilaman. Biz allaqachon razvedkaga borish uchun yetarlicha qurollanganmiz. Agar pulemyot bo'lmasa, unda hech bo'lmaganda asosiy xususiyatlarga ega suv to'pponchasi va stol. :) Keyingi darsda bizni jadvalning to'g'ridan-to'g'ri qo'llanilishi va yozma xossalari uchun integrallarning eng oddiy zararsiz misollari kutmoqda.

Ko‘rishguncha!

Biz hosila koʻp qoʻllanishga ega ekanligini koʻrdik: hosila harakat tezligi (yoki umuman olganda, har qanday jarayonning tezligi); hosila - funksiya grafigiga teginish qiyaligi; lotin yordamida siz funktsiyani monotonlik va ekstremallik uchun tekshirishingiz mumkin; lotin optimallashtirish muammolarini hal qilishga yordam beradi.

Ammo real hayotda biz teskari masalalarni ham hal qilishimiz kerak: masalan, ma'lum harakat qonuni bo'yicha tezlikni topish muammosi bilan bir qatorda, biz ma'lum tezlik bo'yicha harakat qonunini tiklash muammosiga ham duch kelamiz. Keling, ushbu muammolardan birini ko'rib chiqaylik.

1-misol. Moddiy nuqta to'g'ri chiziq bo'ylab harakat qiladi, uning t vaqtdagi tezligi u = tg formula bilan aniqlanadi. Harakat qonunini toping.

Yechim. s = s(t) harakatning istalgan qonuni bo'lsin. Ma'lumki, s"(t) = u"(t). Bu shuni anglatadiki, muammoni hal qilish uchun siz tanlashingiz kerak funktsiyasi s = s(t), uning hosilasi tg ga teng. Buni taxmin qilish qiyin emas

Darhol ta'kidlaymizki, misol to'g'ri hal qilingan, ammo to'liq emas. Biz aniqladikki, aslida muammoning cheksiz ko'p echimlari bor: shaklning har qanday funktsiyasi ixtiyoriy doimiy harakat qonuni bo'lib xizmat qilishi mumkin, chunki

Vazifani aniqroq qilish uchun biz dastlabki vaziyatni tuzatishimiz kerak edi: harakatlanuvchi nuqtaning koordinatasini vaqtning ma'lum bir nuqtasida ko'rsating, masalan, t=0. Agar, deylik, s(0) = s 0 bo‘lsa, u holda tenglikdan s(0) = 0 + C, ya’ni S 0 = C ni olamiz. Endi harakat qonuni yagona aniqlangan:
Matematikada oʻzaro teskari amallarga turli nomlar beriladi va maxsus yozuvlar ixtiro qilinadi: masalan, kvadratlashtirish (x 2) va sinusning kvadrat ildizini olish (sinx) va arksinus(arcsin x) va boshqalar. Berilgan funktsiyaga nisbatan hosilani topish jarayoni differensiatsiya deb ataladi va teskari operatsiya, ya'ni. berilgan hosiladan funktsiyani topish jarayoni - integratsiya.
“Hosila” atamasining o‘zini “kundalik hayotda” oqlash mumkin: y - f(x) funksiyasi yangi y”= f(x) funksiyasini “tug‘adi”. y = f(x) funktsiyasi "ota-ona" , lekin matematiklar, tabiiyki, uni "ota-ona" yoki "ishlab chiqaruvchi" deb atamaydilar, ular buni y" = f "(x) funktsiyasiga nisbatan asosiy tasvir deb aytishadi; qisqacha, antiderivativ.

Ta'rif 1. Agar X dan barcha x uchun F"(x)=f(x) tenglik bajarilsa, y = F(x) funksiya berilgan X oraliqdagi y = f(x) funksiya uchun antiderivativ deyiladi.

Amalda X oralig'i odatda ko'rsatilmaydi, lekin nazarda tutiladi (funktsiyani aniqlashning tabiiy sohasi sifatida).

Mana bir nechta misollar:

1) y = x 2 funksiya y = 2x funksiya uchun anti hosiladir, chunki barcha x uchun (x 2)" = 2x tengligi to'g'ri.
2) y - x 3 funksiya y-3x 2 funksiyasi uchun anti hosiladir, chunki barcha x uchun (x 3)" = 3x 2 tengligi to'g'ri.
3) y-sinx funktsiyasi y = cosx funksiyasi uchun anti hosiladir, chunki barcha x uchun (sinx)" = cosx tengligi to'g'ri.
4) Funksiya oraliqdagi funksiya uchun teskari hosiladir, chunki barcha x > 0 uchun tenglik to‘g‘ri bo‘ladi.
Umuman olganda, hosilalarni topish formulalarini bilgan holda, antiderivativlarni topish uchun formulalar jadvalini tuzish qiyin emas.

Umid qilamizki, siz ushbu jadval qanday tuzilganligini tushunasiz: ikkinchi ustunda yozilgan funktsiyaning hosilasi birinchi ustunning tegishli qatorida yozilgan funktsiyaga teng (tekshiring, dangasa bo'lmang, bu juda foydali). Masalan, y = x 5 funksiyasi uchun antiderivativ, siz aniqlaganingizdek, funktsiyadir (jadvalning to'rtinchi qatoriga qarang).

Eslatmalar: 1. Quyida biz teoremani isbotlaymiz, agar y = F(x) y = f(x) funksiya uchun anti hosila bo‘lsa, u holda y = f(x) funksiya cheksiz ko‘p qarama-qarshi hosilalarga ega va ularning barchasi y = ko‘rinishga ega bo‘ladi. F(x ) + C. Shuning uchun jadvalning ikkinchi ustunining hamma joyiga C atamasini qo'shish to'g'riroq bo'ladi, bu erda C ixtiyoriy haqiqiy sondir.
2. Qisqartirish uchun ba’zan “y = F(x) funksiya y = f(x) funksiyaning anti hosilasidir” iborasi o‘rniga F(x) f(x) ning antihosilasi deyishadi. ”.

2. Antiderivativlarni topish qoidalari

Antiderivativlarni topishda, shuningdek, hosilalarni topishda nafaqat formulalar (ular 196-betdagi jadvalda keltirilgan), balki ba'zi qoidalar ham qo'llaniladi. Ular derivativlarni hisoblashning tegishli qoidalariga bevosita bog'liq.

Bizga ma'lumki, summaning hosilasi uning hosilalari yig'indisiga teng. Ushbu qoida antiderivativlarni topish uchun tegishli qoidani yaratadi.

1-qoida. Yig'indining antiderivativi antiderivativlar yig'indisiga teng.

Sizning e'tiboringizni ushbu formulaning biroz "engilligiga" qaratamiz. Aslida, teoremani shakllantirish kerak: agar y = f(x) va y = g (x) funktsiyalari X oralig'ida mos ravishda y-F(x) va y-G(x) ga qarshi hosilalarga ega bo'lsa, u holda y funktsiyalar yig'indisi. = f(x)+g(x) X oraliqda anti hosilaga ega va bu antihosil y = F(x)+G(x) funksiyadir. Odatda, qoidalarni shakllantirishda (teoremalarni emas) faqat kalit so'zlar qoladi - bu qoidalarni amalda qo'llash uchun qulayroqdir.

2-misol. y = 2x + cos x funksiyaning antihosilini toping.

Yechim. 2x uchun antiderivativ x"; koks uchun antiderivativ sin x. Demak, y = 2x + cos x funksiyasi uchun antiderivativ y = x 2 + sin x funksiyasi bo'ladi (va umuman shaklning har qanday funktsiyasi) Y = x 1 + sinx + C) .
Biz bilamizki, doimiy omilni hosila belgisidan chiqarish mumkin. Bu qoida antiderivativlarni topish uchun tegishli qoidani yaratadi.

2-qoida. Doimiy omilni antiderivativ belgisidan chiqarish mumkin.

3-misol.

Yechim. a) sin x ning antiderivativi -soz x; Demak, y = 5 sin x funksiya uchun anti hosila funksiyasi y = -5 cos x funksiya bo ladi.

b) cos x ga qarshi hosila sin x; Bu funktsiyaning anti hosilasi funktsiya ekanligini anglatadi
v) x 3 ga qarshi hosila x ga qarshi hosila, y = 1 funksiya uchun anti hosila y = x funktsiyadir. Antiderivativlarni topishning birinchi va ikkinchi qoidalaridan foydalanib, y = 12x 3 + 8x-1 funksiya uchun anti hosila funktsiya ekanligini aniqlaymiz.
Izoh. Ma'lumki, mahsulotning hosilasi hosilalarning hosilasiga teng emas (mahsulotni farqlash qoidasi murakkabroq) va qismning hosilasi hosilalarning ko'paytmasiga teng emas. Shuning uchun ko'paytmaning anti hosilasi yoki ikkita funktsiyaning bo'limiga qarshi hosilasini topish qoidalari yo'q. Ehtiyot bo'ling!
Keling, antiderivativlarni topishning yana bir qoidasini olaylik. Bizga ma'lumki, y = f(kx+m) funksiyaning hosilasi formula bo'yicha hisoblanadi

Bu qoida antiderivativlarni topish uchun tegishli qoidani yaratadi.
3-qoida. Agar y = F(x) y = f(x) funksiya uchun anti hosila bo lsa, u holda y=f(kx+m) funksiya uchun anti hosila funktsiya bo ladi.

Aslida,

Demak, u y = f(kx+m) funksiyaga qarshi hosiladir.
Uchinchi qoidaning ma'nosi quyidagicha. Agar y = f(x) funksiyaning anti hosilasi y = F(x) funksiya ekanligini bilsangiz va y = f(kx+m) funksiyaning antihosilini topishingiz kerak bo‘lsa, quyidagi amallarni bajaring: xuddi shu funksiya F, lekin x argumenti o‘rniga kx+m ifodasini qo‘ying; Bundan tashqari, funktsiya belgisidan oldin "tuzatish omili" ni yozishni unutmang
4-misol. Berilgan funksiyalar uchun antiderivativlarni toping:

Yechim, a) sin x ga qarshi hosila -soz x; Bu shuni anglatadiki, y = sin2x funksiya uchun antiderivativ funktsiya bo'ladi
b) cos x ga qarshi hosila sin x; Bu funktsiyaning anti hosilasi funktsiya ekanligini anglatadi

c) x 7 ga qarshi hosila y = (4-5x) 7 funksiya uchun anti hosila funktsiya bo'lishini anglatadi.

3. Noaniq integral

Yuqorida berilgan y = f(x) funksiya uchun anti hosilani topish masalasi bir nechta yechimga ega ekanligini yuqorida qayd etgan edik. Keling, bu masalani batafsilroq muhokama qilaylik.

Isbot. 1. X oraliqda y = f(x) funksiya uchun y = F(x) anti hosilasi bo‘lsin. Demak, X dan barcha x uchun x"(x) = f(x) tenglik amal qiladi. Keling, y = F(x)+C ko‘rinishdagi istalgan funksiyaning hosilasini toping:
(F(x) +C) = F"(x) +C = f(x) +0 = f(x).

Demak, (F(x)+C) = f(x). Demak, y = F(x) + C y = f(x) funksiya uchun anti hosiladir.
Shunday qilib, biz isbotladikki, agar y = f(x) funksiya y=F(x) qarama-qarshi hosilaga ega bo‘lsa, u holda (f = f(x) funktsiyaning cheksiz ko‘p anti hosilalari, masalan, y = ko‘rinishdagi istalgan funksiya mavjud. F(x) +C antiderivativ hisoblanadi.
2. Endi ko'rsatilgan turdagi funksiyalar butun antiderivativlar to'plamini tugatishini isbotlaylik.

X oraliqda Y = f(x) funksiya uchun y=F 1 (x) va y=F(x) ikkita qarama-qarshi hosila bo‘lsin. Demak, X oralig‘idagi barcha x uchun quyidagi munosabatlar amal qiladi: F^ ( x) = f (X); F"(x) = f(x).

y = F 1 (x) -.F(x) funksiyani ko‘rib chiqamiz va uning hosilasini topamiz: (F, (x) -F(x))" = F[(x)-F(x) = f(x) ) - f(x) = 0.
Ma'lumki, agar funktsiyaning X oralig'idagi hosilasi xuddi shunday nolga teng bo'lsa, u holda funksiya X oralig'ida doimiy bo'ladi (35-§ dan 3-teoremaga qarang). Bu shuni anglatadiki, F 1 (x) - F (x) = C, ya'ni. Fx) = F(x)+C.

Teorema isbotlangan.

5-misol. Tezlikning vaqt bo'yicha o'zgarishi qonuni berilgan: v = -5sin2t. Agar t=0 vaqtda nuqta koordinatasi 1,5 soniga (ya’ni s(t) = 1,5) teng bo‘lganligi ma’lum bo‘lsa, s = s(t) harakat qonunini toping.

Yechim. Tezlik koordinataning vaqtga bog'liq hosilasi bo'lgani uchun, avvalo tezlikning antiderivativini topishimiz kerak, ya'ni. v = -5sin2t funksiyasi uchun antihosil. Bunday antiderivativlardan biri funktsiya bo'lib, barcha antiderivativlar to'plami quyidagi ko'rinishga ega:

S doimiysining xususiy qiymatini topish uchun biz boshlang'ich shartlardan foydalanamiz, unga ko'ra s(0) = 1,5. Formula (1) ga t=0, S = 1,5 qiymatlarini qo‘yib, biz quyidagilarni olamiz:

Topilgan C qiymatini (1) formulaga qo'yib, bizni qiziqtirgan harakat qonunini olamiz:

Ta'rif 2. Agar y = f(x) funksiya X oraliqda y = F(x) ga qarshi hosilaga ega bo‘lsa, u holda barcha antiderivativlar to‘plami, ya’ni. y = F(x) + C ko‘rinishdagi funksiyalar to‘plami y = f(x) funksiyaning noaniq integrali deyiladi va quyidagi bilan belgilanadi:

(o'qing: "x de x dan noaniq integral ef").
Keyingi xatboshida biz ushbu belgining yashirin ma'nosi nima ekanligini bilib olamiz.
Ushbu bo'limda mavjud bo'lgan antiderivativlar jadvaliga asoslanib, biz asosiy noaniq integrallar jadvalini tuzamiz:

Antiderivativlarni topish uchun yuqoridagi uchta qoidaga asoslanib, biz mos keladigan integratsiya qoidalarini shakllantirishimiz mumkin.

1-qoida. Funktsiyalar yig'indisining integrali ushbu funktsiyalarning integrallari yig'indisiga teng:

2-qoida. Doimiy omil integral belgisidan chiqarilishi mumkin:

3-qoida. Agar

6-misol. Noaniq integrallarni toping:

Yechim, a) Integrasiyaning birinchi va ikkinchi qoidalaridan foydalanib, biz quyidagilarni olamiz:

Endi 3 va 4 integratsiya formulalaridan foydalanamiz:

Natijada biz quyidagilarni olamiz:

b) Integrasiyaning uchinchi qoidasi va 8-formuladan foydalanib, biz quyidagilarni olamiz:

v) Berilgan integralni to'g'ridan-to'g'ri topish uchun bizda mos formula ham, tegishli qoida ham mavjud emas. Bunday hollarda, ba'zan integral belgisi ostida joylashgan ifodani ilgari bajarilgan bir xil o'zgartirishlar yordam beradi.