Paralelograma pretējo leņķu īpašības. Paralelograma diagonāļu īpašība

Pa-ral-le-lo-gram-ma pazīmes

1. Paralelograma definīcija un pamatīpašības

Sāksim ar to, ka atceramies pa-ral-le-lo-gram-ma definīciju.

Definīcija. Paralēlogramma- four-you-rekh-coal-nick, kāds-ro-go ir divas pro-ti-on-false puses para-ral-lel-ny (sk. Att. . vienu).

Rīsi. 1. Pa-ral-le-lo-gram

Atsaukt jaunas pa-ral-le-lo-gram-ma īpašības:

Lai varētu izmantot visas šīs īpašības, jums ir jābūt pārliecinātam, ka fi-gu-ra, ak kāds -Roy jautājumā, - pa-ral-le-lo-gram. Lai to izdarītu, ir jāzina tādi fakti kā pa-ral-le-lo-gram-ma pazīmes. Pirmos divus no tiem mēs skatāmies šodien.

2. Paralelograma pirmā zīme

Teorēma. Pirmā pa-ral-le-lo-gram-ma zīme. Ja četri-jūs-rekh-coal-ni-ke divas pro-ti-in-false puses ir vienādas un par-ral-lel-na, tad šis four-you-rekh-coal- segvārds - paralelograms. .

Rīsi. 2. Pirmā pa-ral-le-lo-gram-ma zīme

Pierādījums. We-we-we-dem in four-rekh-coal-ni-ke dia-go-nal (sk. 2. att.), viņa sadalīja to divos trīsstūros-no-ka. Pierakstiet, ko mēs zinām par šiem trijstūriem:

saskaņā ar pirmo trīsstūru vienādības zīmi.

No norādīto trīsstūru vienādības izriet, ka saskaņā ar taisnu līniju par-ral-lel-no-sti zīmi, kad atkārtoti se- che-ni to se-ku-schey. Mums ir tas:

Pirms-par-bet.

3. Paralelograma otrā zīme

Teorēma. Otrais bars ir pa-ral-le-lo-gram-ma zīme. Ja četri-jūs-rekh-coal-ni-ke katras divas pro-ti-in-false puses ir vienādas, tad šis four-you-rekh-coal-nick - paralelograms. .

Rīsi. 3. Otrā spieta zīme pa-ral-le-lo-gram-ma

Pierādījums. We-we-we-dem in four-you-rekh-coal-ni-ke dia-go-nal (sk. 3. att.), viņa sadala to divos trīsstūros-no-ka. Mēs rakstām to, ko zinām par šiem trijstūriem, pamatojoties uz for-mu-li-ditch-ki theo-re-we:

saskaņā ar trešo trīsstūru vienādības zīmi.

No trijstūra vienādības izriet, ka saskaņā ar zīmi par-ral-lel-no-sti taisnām līnijām, kad atkārtoti se-che-ing tos se-ku-schey. By-lu-cha-eat:

pa-ral-le-lo-gram saskaņā ar definīciju-de-le-ny. Q.E.D.

Pirms-par-bet.

4. Paralelograma pirmās pazīmes izmantošanas piemērs

Ras-apskatiet pa-ral-le-lo-gram-ma zīmju pielietošanas piemēru.

1. piemērs. In you-far-scrap-che-you-rex-coal-no-ke Atrodiet: a) četru-jūsu-reksu-ogļu-no-ka stūrus; b) simtro-aka.

Lēmums. Attēls-ra-ziema Att. 4.

pa-ral-le-lo-gram saskaņā ar pirmo zīmi-ku pa-ral-le-lo-gram-ma.

BET. saskaņā ar para-le-lo-gram-ma īpašību par pro-ti-in-viltus-leņķiem, saskaņā ar para-le-lo-gram-ma īpašību par leņķu summu, kas atbilst vienam pusē.

B. ar īpašību pro-ty-in-on-false pušu vienlīdzība.

re-at-sign pa-ral-le-lo-gram-ma

5. Atkārtošana: paralelograma definīcija un īpašības

Atgādinot, ka paralelograms- tas ir četri-jūs-rekh-ogļu niks, kādam ir pro-ti-on-false puses pārī-bet-pa-ral-lel-na. Tas ir, ja - pa-ral-le-lo-gram, tad (Skatīt 1. att.).

Pa-ral-le-lo-gram ir virkne īpašību: pro-ti-in-false leņķi ir vienādi (), pro-ti-on-false simts-ro - mēs esam vienādi ( ). Turklāt dia-go-on-vai par-ral-le-lo-gram-ma punktā re-se-che-niya de-lyat-by-lam, leņķu summa, at-le- pa-ral-le-lo-gram-ma, vienāds ar jebkuru pusi, vienāds utt.

Bet, lai izmantotu visas šīs īpašības, ir jābūt ab-so-lute-bet pārliecinātiem-mēs, ka sacīkstēs ri-va-e-my che-you-rekh-coal-nick - pa-ral-le- lo-gram. Šim nolūkam ir pazīmes par-ral-le-lo-gram-ma: tas ir, tie fakti, no kuriem var izdarīt vienvērtīgu secinājumu, ka che-you-rekh-coal-nick yav-la-et -sja pa-ral-le-lo-gram-mamma. Iepriekšējā nodarbībā mēs jau esam apsvēruši divas funkcijas. Šo stundu mēs skatāmies uz trešo.

6. Paralelograma trešā pazīme un tās pierādījums

Ja in four-you-rekh-coal-ni-ke dia-go-na-li vietā re-se-che-niya de-lyat-by-lam, tad šis four-you-reh-coal-nick yav-la-et-sya pa-ral-le-lo-gram-mom.

Ņemot vērā:

Che-you-reh-coal-nick; ; .

Pierādīt:

Paralēlogramma.

Pierādījums:

Lai pierādītu šo faktu, ir jāpierāda pa-ral-le-lo-gram-ma malu para-ral-lel-ness. Un taisnu līniju par-ral-lel-ness visbiežāk ir līdz-ka-zy-va-et-sya, izmantojot iekšējo leņķu līdz šķērsām, kas atrodas šajās taisnēs. Tādā veidā na-pra-shi-va-et-sya nākamo-du-u-sche ceļu uz-ka-for-tel-stva no trešās zīmes-of-pa-ral -le-lo-gram- ma: caur trīsstūru vienādību-ni-kov .

Gaidīsim šo trīsstūru vienādību. Patiešām, no nosacījuma izriet:. Turklāt, tā kā leņķi ir vertikāli, tie ir vienādi. T.i.:

(pirmā vienlīdzības zīmetrīsstūrveida-ni-kov- divi simti rousu un leņķis starp tiem).

No trīsstūru vienādības: (jo iekšējie leņķi uz krusta ir vienādi šajās taisnēs un se-ku-schey). Turklāt no trīsstūru vienādības izriet, ka. Tas nozīmē, ka mēs esam, piemēram, chi-li, ka četrās-jūs-rekh-coal-ni-ke divas puses ir vienādas un par-ral-lel-na. Pēc pirmās zīmes pa-ral-le-lo-gram-ma: - pa-ral-le-lo-gram.

Pirms-par-bet.

7. Paralelograma trešās pazīmes uzdevuma piemērs un vispārinājums

Ras-apskatiet trešās zīmes para-ral-le-lo-gram-ma pielietojuma piemēru.

1. piemērs

Ņemot vērā:

- paralelograms; . - se-re-di-na, - se-re-di-na, - se-re-di-na, - se-re-di-na (skat. 2. att.).

Pierādīt:- pa-ral-le-lo-gram.

Pierādījums:

Tātad, in four-you-rekh-coal-no-ke dia-go-na-li vietā re-se-che-niya de-lyat-sya-by-lam. Saskaņā ar trešo zīmi, pa-ral-le-lo-gram-ma, no tā izriet, ka - pa-ral-le-lo-gram.

Pirms-par-bet.

Ja analizējam pa-ral-le-lo-gram-ma trešo zīmi, tad mēs varam pamanīt, ka šai zīmei ir co-ot-reply- ir par-ral-le-lo-gram-ma īpašība. Tas ir, fakts, ka dia-go-na-vai viņi de-lyat-by-lam, is-la-et-sya nav tikai pa-ral-le-lo-gram-ma īpašums, un tā no -li-chi-tel-nym, ha-rak-te-ri-sti-che-sky īpašums, saskaņā ar dažiem-ro-mu to var izliet no daudziem che-you-reh-coal-no- kov.

AVOTS

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://www.tepka.ru/geometriya/16.1.gif

Šodienas nodarbībā mēs atkārtosim paralelograma galvenās īpašības, un pēc tam pievērsīsim uzmanību pirmo divu paralelograma pazīmju izskatīšanai un pierādīsim tās. Pierādīšanas gaitā atgādināsim par trijstūra vienādības zīmju pielietojumu, ko pētījām pagājušajā gadā un atkārtojām pirmajā nodarbībā. Beigās tiks sniegts piemērs par paralelograma pētīto pazīmju pielietojumu.

Tēma: Četrstūri

Nodarbība: Paralelograma zīmes

Sāksim, atgādinot paralelograma definīciju.

Definīcija. Paralēlogramma- četrstūris, kurā katras divas pretējās malas ir paralēlas (sk. 1. att.).

Rīsi. 1. Paralelogramma

Atcerēsimies paralelograma pamatīpašības:

Lai varētu izmantot visas šīs īpašības, jābūt pārliecinātai, ka attiecīgais skaitlis ir paralelograms. Lai to izdarītu, jums jāzina tādi fakti kā paralelograma zīmes. Šodien mēs izskatīsim pirmos divus no tiem.

Teorēma. Pirmā paralelograma pazīme. Ja četrstūrī divas pretējās malas ir vienādas un paralēlas, tad šis četrstūris ir paralelograms. .

Rīsi. 2. Paralelograma pirmā zīme

Pierādījums. Iezīmēsim četrstūrī diagonāli (skat. 2. att.), viņa to sadalīja divos trīsstūros. Pierakstīsim, ko zinām par šiem trijstūriem:

saskaņā ar pirmo trīsstūru vienādības zīmi.

No šo trīsstūru vienādības izriet, ka, pamatojoties uz līniju paralēlismu to sekanta krustpunktā. Mums ir tas:

Pierādīts.

Teorēma. Otrā paralelograma zīme. Ja četrstūrī katras divas pretējās malas ir vienādas, tad šis četrstūris ir paralelograms. .

Rīsi. 3. Paralelograma otrā zīme

Pierādījums. Ievelkam četrstūrī diagonāli (skat. 3. att.), tā sadala to divos trīsstūros. Uzrakstīsim, ko zinām par šiem trijstūriem, pamatojoties uz teorēmas formulējumu:

saskaņā ar trešo trīsstūru vienādības kritēriju.

No trijstūra vienādības izriet, ka, pamatojoties uz paralēlām taisnēm to sekanta krustpunktā. Mēs iegūstam:

paralelograms pēc definīcijas. Q.E.D.

Pierādīts.

Apskatīsim piemēru paralelograma pazīmju pielietošanai.

Piemērs 1. Izliektā četrstūrī Atrast: a) četrstūra stūrus; b) sānu.

Lēmums. Attēlosim att. 4.

Rīsi. 4

paralelograms atbilstoši pirmajam paralelograma atribūtam.

Paralelograma jēdziens

1. definīcija

Paralēlogramma ir četrstūris, kura pretējās malas ir paralēlas viena otrai (1. att.).

1. attēls.

Paralelogramam ir divas galvenās īpašības. Apskatīsim tos bez pierādījumiem.

1. īpašums: Paralelograma pretējās malas un leņķi ir attiecīgi vienādi viens ar otru.

2. īpašums: Paralelogramā novilktās diagonāles sadala uz pusēm pēc to krustpunkta.

Paralelogrammas iezīmes

Apsveriet trīs paralelograma pazīmes un izklāstiet tās teorēmu veidā.

1. teorēma

Ja četrstūra divas malas ir vienādas viena ar otru un arī paralēlas, tad šis četrstūris būs paralelograms.

Pierādījums.

Dosim mums četrstūri $ABCD$. Kurā $AB||CD$ un $AB=CD$ Uzzīmēsim tajā diagonāli $AC$ (2. att.).

2. attēls.

Apsveriet paralēlās līnijas $AB$ un $CD$ un to sekantu $AC$. Tad

\[\angle CAB=\angle DCA\]

kā šķērsām stūri.

Saskaņā ar $I$ trijstūra vienādības kritēriju,

jo $AC$ ir to kopējā puse un $AB=CD$ pēc pieņēmuma. Līdzekļi

\[\angle DAC=\angle ACB\]

Apsveriet taisnes $AD$ un $CB$ un to sekantu $AC$, ar pēdējo šķērsleņķu vienādību iegūstam, ka $AD||CB$.) Tāpēc pēc $1$ definīcijas šis četrstūris ir paralelograms.

Teorēma ir pierādīta.

2. teorēma

Ja četrstūra pretējās malas ir vienādas, tad tas ir paralelograms.

Pierādījums.

Dosim mums četrstūri $ABCD$. Kurā $AD=BC$ un $AB=CD$. Uzzīmēsim tajā diagonāli $AC$ (3. att.).

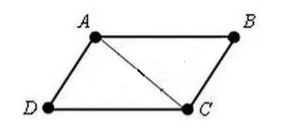
3. attēls

Tā kā $AD=BC$, $AB=CD$ un $AC$ ir kopīga puse, tad ar $III$ trīsstūra vienādības testu,

\[\trijstūris DAC=\trijstūris ACB\]

\[\angle DAC=\angle ACB\]

Apsveriet līnijas $AD$ un $CB$ un to sekantu $AC$, pēc pēdējās šķērsenisko leņķu vienādības iegūstam $AD||CB$. Tāpēc pēc definīcijas $1$ šis četrstūris ir paralelograms.

\[\angle DCA=\angle CAB\]

Apsveriet līnijas $AB$ un $CD$ un to sekantu $AC$, ar pēdējo šķērsleņķu vienādību iegūstam $AB||CD$. Tāpēc saskaņā ar 1. definīciju šis četrstūris ir paralelograms.

Teorēma ir pierādīta.

3. teorēma

Ja četrstūrī ievilktās diagonāles pēc to krustpunkta sadala divās vienādās daļās, tad šis četrstūris ir paralelograms.

Pierādījums.

Dosim mums četrstūri $ABCD$. Uzzīmēsim tajā diagonāles $AC$ un $BD$. Ļaujiet tiem krustoties punktā $O$ (4. att.).

4. attēls

Tā kā saskaņā ar nosacījumu $BO=OD,\AO=OC$ un leņķi $\angle COB=\angle DOA$ ir vertikāli, tad, izmantojot $I$ trīsstūra vienādības testu,

\[\trijstūris BOC=\trijstūris AOD\]

\[\angle DBC=\angle BDA\]

Apsveriet līnijas $BC$ un $AD$ un to sekantu $BD$, pēc pēdējās šķērsvirziena leņķu vienādības iegūstam $BC||AD$. Arī $BC=AD$. Tāpēc saskaņā ar teorēmu $1$ šis četrstūris ir paralelograms.

Paralelograms ir četrstūris, kura pretējās malas ir pa pāriem paralēlas. Nākamajā attēlā parādīts paralelograms ABCD. Tam ir AB mala paralēla malai CD un mala BC paralēla malai AD.

Kā jūs, iespējams, uzminējāt, paralelograms ir izliekts četrstūris. Apsveriet paralelograma pamatīpašības.

Paralelogrammas īpašības

1. Paralelogramā pretējie leņķi un pretējās malas ir vienādi. Pierādīsim šo īpašību - apskatīsim paralelogramu, kas parādīts nākamajā attēlā.

Diagonālā BD sadala to divās daļās vienāds trīsstūris: ABD un CBD. Tie ir vienādi malās BD un divos tai blakus esošajos leņķos, jo leņķi, kas atrodas pie BD sekanta, ir attiecīgi paralēlas taisnes BC un AD un AB un CD. Tāpēc AB = CD un
BC = AD. Un no leņķu 1, 2, 3 un 4 vienādības izriet, ka leņķis A = leņķis1 + leņķis3 = leņķis2 + leņķis4 = leņķis C.

2. Paralelograma diagonāles sadala uz pusēm ar krustpunktu. Pieņemsim, ka punkts O ir paralelograma ABCD diagonāļu AC un BD krustpunkts.

Tad trijstūris AOB un trijstūris COD ir vienādi viens ar otru, gar malu un diviem tai blakus esošajiem leņķiem. (AB=CD, jo tās ir paralelograma pretējās malas. Un leņķis1 = leņķis2 un leņķis3 = leņķis4 kā krusteniski guļus leņķi taisnes AB un CD krustpunktā attiecīgi ar sekantiem AC un BD.) No tā izriet, ka AO = OC un OB = OD, kas un bija jāpierāda.

Visas galvenās īpašības ir attēlotas sekojošos trīs attēlos.

Svarīgas piezīmes!
1. Ja formulu vietā redzat abrakadabra, iztīriet kešatmiņu. Šeit ir rakstīts, kā to izdarīt savā pārlūkprogrammā:
2. Pirms sākat lasīt rakstu, pievērsiet uzmanību mūsu navigatoram noderīgs resurss priekš

1. Paralelogramma

Salikts vārds "paralēlogramma"? Un aiz tā ir ļoti vienkārša figūra.

Tas ir, mēs paņēmām divas paralēlas līnijas:

Šķērso vēl divi:

Un iekšā - paralelograms!

Kādas ir paralelograma īpašības?

Paralelogrammas īpašības.

Tas ir, ko var izmantot, ja uzdevumā ir dots paralelograms?

Uz šo jautājumu atbild šāda teorēma:

Uzzīmēsim visu sīkāk.

Ko dara teorēmas pirmais punkts? Un tas, ka, ja tev IR paralelograms, tad katrā ziņā

Otrā rindkopa nozīmē, ka, ja ir paralelograms, tad atkal noteikti:

Visbeidzot, trešais punkts nozīmē, ka, ja jums IR paralelograms, pārliecinieties:

Redziet, kāda ir izvēles bagātība? Ko izmantot uzdevumā? Centieties koncentrēties uz uzdevuma jautājumu vai vienkārši izmēģiniet visu pēc kārtas - kaut kāda “atslēga” noderēs.

Un tagad uzdosim sev vēl vienu jautājumu: kā atpazīt paralelogramu "sejā"? Kam jānotiek ar četrstūri, lai mums būtu tiesības tam piešķirt paralelograma “nosaukumu”?

Uz šo jautājumu atbild vairākas paralelograma zīmes.

Paralelograma pazīmes.

Uzmanību! Sāciet.

Paralēlogramma.

Pievērsiet uzmanību: ja savā uzdevumā esat atradis kaut vienu zīmi, tad jums ir tieši paralelograms, un jūs varat izmantot visas paralelograma īpašības.

2. Taisnstūris

Es domāju, ka tas tev vispār nebūs jaunums.

Pirmais jautājums ir: vai taisnstūris ir paralelograms?

Protams tas ir! Galu galā viņam ir - atcerieties, mūsu zīme 3?

Un no šejienes, protams, izriet, ka taisnstūrim, tāpat kā jebkuram paralelogramam, un, un diagonāles tiek dalītas ar krustošanās punktu uz pusēm.

Bet ir taisnstūris un viena atšķirīga īpašība.

Taisnstūra īpašums

Kāpēc šis īpašums ir atšķirīgs? Jo nevienam citam paralelogramam nav vienādas diagonāles. Noformulēsim to skaidrāk.

Pievērsiet uzmanību: lai četrstūris kļūtu par taisnstūri, tam vispirms jākļūst par paralelogramu un pēc tam jāuzrāda diagonāļu vienādība.

3. Dimants

Un atkal jautājums: vai rombs ir paralelograms vai nav?

Ar pilnu labo - paralelograms, jo tam ir un (atcerieties mūsu zīmi 2).

Un atkal, tā kā rombs ir paralelograms, tad tam ir jābūt visām paralelograma īpašībām. Tas nozīmē, ka romba pretējie leņķi ir vienādi, pretējās malas ir paralēlas, un diagonāles sadala uz pusēm ar krustošanās punktu.

Romba īpašības

Skaties uz bildi:

Tāpat kā taisnstūra gadījumā, šīs īpašības ir atšķirīgas, tas ir, katrai no šīm īpašībām mēs varam secināt, ka mums nav tikai paralelograms, bet gan rombs.

Romba pazīmes

Un vēlreiz pievērsiet uzmanību: jābūt ne tikai četrstūrim ar perpendikulārām diagonālēm, bet gan paralelogramam. Pārliecinies:

Nē, protams, nē, lai gan tā diagonāles un ir perpendikulāras, un diagonāle ir leņķu bisektrise u. Bet ... diagonāles nedalās, krustošanās punkts uz pusēm, tātad - NAV paralelograms, un tāpēc NAV rombs.

Tas ir, kvadrāts ir taisnstūris un rombs vienlaikus. Redzēsim, kas no tā iznāks.

Vai ir skaidrs, kāpēc? - rombs - leņķa A bisektrise, kas ir vienāda ar. Tātad tas sadalās (un arī) divos leņķos.

Nu, tas ir pilnīgi skaidrs: taisnstūra diagonāles ir vienādas; romba diagonāles ir perpendikulāras, un vispār - paralelogramu diagonāles tiek dalītas ar krustošanās punktu uz pusēm.

VIDĒJS LĪMENIS

Četrstūru īpašības. Paralēlogramma

Paralelogrammas īpašības

Uzmanību! Vārdi " paralelogramu īpašības» nozīmē, ka, ja jums ir uzdevums tur ir paralelograms, tad var izmantot visu tālāk minēto.

Teorēma par paralelograma īpašībām.

Jebkurā paralelogramā:

Redzēsim, kāpēc tā ir taisnība, citiem vārdiem sakot MĒS PIERĀDĪSIM teorēma.

Tātad, kāpēc 1) ir taisnība?

Tā kā tas ir paralelograms, tad:

• kā guļ krustu šķērsu
• kā guļ pāri.

Tādējādi (pamatojoties uz II: un - vispārīgi.)

Nu tad vienreiz - tas tā! - pierādījās.

Bet starp citu! Mēs arī pierādījām 2)!

Kāpēc? Bet galu galā (skatieties uz attēlu), tas ir, proti, tāpēc, ka.

Atlikuši tikai 3).

Lai to izdarītu, jums joprojām ir jāvelk otrā diagonāle.

Un tagad mēs to redzam - saskaņā ar II zīmi (leņķis un sānu "starp" tiem).

Īpašības pierādītas! Pāriesim pie zīmēm.

Paralelogrammas iezīmes

Atgādiniet, ka paralelograma zīme atbild uz jautājumu "kā to uzzināt?", ka figūra ir paralelograms.

Ikonās tas ir šādi:

Kāpēc? Būtu jauki saprast, kāpēc – ar to pietiek. Bet paskaties:

Nu, mēs sapratām, kāpēc 1. zīme ir patiesa.

Nu, tas ir vēl vienkāršāk! Atkal zīmēsim diagonāli.

Kas nozīmē:

Un ir arī viegli. Bet... savādāk!

Nozīmē,. Oho! Bet arī - iekšējais vienpusējs pie sekanta!

Tāpēc fakts, kas nozīmē, ka.

Un ja skatās no otras puses, tad tie ir iekšēji vienpusēji pie sekanta! Un tāpēc.

Redzi, cik tas ir lieliski?!

Un atkal vienkārši:

Tieši tas pats, un.

Pievērs uzmanību: ja atradi vismaz viena paralelograma zīme jūsu uzdevumā, tad jums ir tieši tā paralelograms un jūs varat izmantot visi paralelograma īpašības.

Lai iegūtu pilnīgu skaidrību, skatiet diagrammu:

Četrstūru īpašības. Taisnstūris.

Taisnstūra īpašības:

Punkts 1) ir diezgan acīmredzams - galu galā zīme 3 () ir vienkārši izpildīta

Un punkts 2) - ļoti svarīgs. Tāpēc pierādīsim to

Tātad, uz divām kājām (un - vispārīgi).

Nu, tā kā trīsstūri ir vienādi, tad arī to hipotenūzas ir vienādas.

To pierādīja!

Un iedomājieties diagonāļu vienādību - atšķirīgā iezīme tieši taisnstūris starp visiem paralelogramiem. Tas ir, sekojošais apgalvojums ir patiess

Paskatīsimies, kāpēc?

Tātad, (kas nozīmē paralelograma leņķus). Bet vēlreiz atcerieties, ka - paralelograms, un tāpēc.

Nozīmē,. Un, protams, no tā izriet, ka katrs no tiem Galu galā tādā daudzumā, kādā viņiem vajadzētu dot!

Šeit mēs esam pierādījuši, ka, ja paralelograms pēkšņi (!) būs vienādas diagonāles, tad šis tieši taisnstūris.

Bet! Pievērs uzmanību! Tas ir par paralelogrami! Nav nevienačetrstūris ar vienādām diagonālēm ir taisnstūris un tikai paralelograms!

Četrstūru īpašības. Rombs

Un atkal jautājums: vai rombs ir paralelograms vai nav?

Ar pilnu labo - paralelograms, jo tam ir un (Atcerieties mūsu zīmi 2).

Un atkal, tā kā rombs ir paralelograms, tam ir jābūt visām paralelograma īpašībām. Tas nozīmē, ka romba pretējie leņķi ir vienādi, pretējās malas ir paralēlas, un diagonāles sadala uz pusēm ar krustošanās punktu.

Bet ir arī īpašas īpašības. Mēs formulējam.

Romba īpašības

Kāpēc? Tā kā rombs ir paralelograms, tad tā diagonāles tiek sadalītas uz pusēm.

Kāpēc? Jā, tieši tāpēc!

Citiem vārdiem sakot, diagonāles un izrādījās romba stūru bisektrise.

Tāpat kā taisnstūra gadījumā, šīs īpašības ir īpatnējs, katrs no tiem ir arī romba zīme.

Romba zīmes.

Kāpēc ir tā, ka? Un paskaties

Līdz ar to, un ganšie trīsstūri ir vienādsānu.

Lai četrstūris būtu rombs, tam vispirms "jākļūst" par paralelogramu, un tad jau jādemonstrē 1. vai 2. pazīme.

Četrstūru īpašības. Kvadrāts

Tas ir, kvadrāts ir taisnstūris un rombs vienlaikus. Redzēsim, kas no tā iznāks.

Vai ir skaidrs, kāpēc? Kvadrāts - rombs - leņķa bisektrise, kas ir vienāda ar. Tātad tas sadalās (un arī) divos leņķos.

Nu, tas ir pilnīgi skaidrs: taisnstūra diagonāles ir vienādas; romba diagonāles ir perpendikulāras, un vispār - paralelogramu diagonāles tiek dalītas ar krustošanās punktu uz pusēm.

Kāpēc? Vienkārši piemērojiet Pitagora teorēmu.

KOPSAVILKUMS UN PAMATFORMULA

Paralelogrammas īpašības:

1. Pretējās puses ir vienādas: , .
2. Pretējie leņķi ir: , .
3. Leņķi vienā pusē kopā veido: , .
4. Diagonāles ar krustošanās punktu dala uz pusēm: .

Taisnstūra īpašības:

1. Taisnstūra diagonāles ir: .
2. Taisnstūris ir paralelograms (taisnstūrim ir izpildītas visas paralelograma īpašības).

Romba īpašības:

1. Romba diagonāles ir perpendikulāras: .
2. Romba diagonāles ir tā leņķu bisektrise: ; ; ; .
3. Rombs ir paralelograms (rombam ir izpildītas visas paralelograma īpašības).

Kvadrātveida īpašības:

Kvadrāts ir vienlaikus rombs un taisnstūris, tāpēc kvadrātam ir izpildītas visas taisnstūra un romba īpašības. Kā arī:

Nu tēma beigusies. Ja tu lasi šīs rindas, tad tu esi ļoti foršs.

Jo tikai 5% cilvēku spēj kaut ko apgūt paši. Un ja esi izlasījis līdz galam, tad esi 5% robežās!

Tagad pats svarīgākais.

Jūs esat izdomājis teoriju par šo tēmu. Un, es atkārtoju, tas ir ... tas ir vienkārši super! Jūs jau esat labāks par lielāko daļu jūsu vienaudžu.

Problēma ir tāda, ka ar to var nepietikt...

Par ko?

Priekš veiksmīga piegāde Vienotais valsts eksāmens, uzņemšanai institūtā par budžetu un, PATS SVARĪGI, uz mūžu.

Es jūs ne par ko nepārliecināšu, teikšu tikai vienu...

Cilvēki, kuri saņēma laba izglītība, nopelna daudz vairāk nekā tie, kuri to nesaņēma. Tā ir statistika.

Bet tas nav galvenais.

Galvenais, ka viņi ir LAIMĪGĀK (ir tādi pētījumi). Varbūt tāpēc, ka viņu priekšā paveras daudz vairāk iespēju un dzīve kļūst gaišāka? Nezinu...

Bet padomājiet paši...

Kas nepieciešams, lai pārliecinātos, ka eksāmenā būtu labāks par citiem un galu galā būtu... laimīgāks?

PIEPILDĪT ROKU, RISINOT PROBLĒMAS PAR ŠO TĒMU.

Eksāmenā jums netiks jautāta teorija.

Jums būs nepieciešams atrisināt problēmas laikā.

Un, ja neesi tos atrisinājis (DAUDZ!), tad noteikti kaut kur pieļausi stulbu kļūdu vai vienkārši nepieļausi laikus.

Tas ir kā sportā – vajag vairākas reizes atkārtot, lai noteikti uzvarētu.

Atrodiet kolekciju jebkurā vietā obligāti ar risinājumiem detalizēta analīze un izlem, lem, lem!

Jūs varat izmantot mūsu uzdevumus (nav nepieciešams), un mēs tos noteikti iesakām.

Lai izmantotu mūsu uzdevumus, jums jāpalīdz pagarināt tās YouClever mācību grāmatas kalpošanas laiku, kuru pašlaik lasāt.

Kā? Ir divas iespējas:

1. Atbloķējiet piekļuvi visiem slēptajiem uzdevumiem šajā rakstā -
2. Atbloķējiet piekļuvi visiem slēptajiem uzdevumiem visos 99 apmācības rakstos - Pērciet mācību grāmatu - 499 rubļi

Jā, mums mācību grāmatā ir 99 šādi raksti un uzreiz var atvērt visus uzdevumus un visus tajos slēptos tekstus.

Piekļuve visiem slēptajiem uzdevumiem tiek nodrošināta visu vietnes darbības laiku.

Noslēgumā...

Ja jums nepatīk mūsu uzdevumi, atrodiet citus. Tikai neapstājieties ar teoriju.

“Sapratu” un “Es zinu, kā atrisināt” ir pilnīgi atšķirīgas prasmes. Tev vajag abus.

Atrodi problēmas un atrisini!