Pamatelementu funkcijas un to īpašības. Funkciju pamatīpašības

Pilns pamata elementāro funkciju saraksts

Pamata elementāro funkciju klasē ietilpst:

1. Konstante funkcija $y=C$, kur $C$ ir konstante. Šāda funkcija ņem tādu pašu vērtību $C$ jebkuram $x$.
2. Spēka funkcija $y=x^(a) $, kur eksponents $a$ ir reāls skaitlis.
3. Eksponenciālā funkcija $y=a^(x) $, kur bāze ir grāds $a>0$, $a\ne 1$.
4. Logaritmiskā funkcija $y=\log _(a) x$, kur logaritma bāze ir $a>0$, $a\ne 1$.
5. Trigonometriskās funkcijas $y=\sin x$, $y=\cos x$, $y=tg\, x$, $y=ctg\, x$, $y=\sec x$, $y=A>\ sek\,x$.
6. Apgrieztās trigonometriskās funkcijas $y=\arcsin x$, $y=\arccos x$, $y=arctgx$, $y=arcctgx$, $y=arc\sec x$, $y=arc\, \cos ec\ , x$.

Jaudas funkcijas

Mēs apsvērsim pakāpju funkcijas $y=x^(a) $ uzvedību tajos vienkāršākos gadījumos, kad tās eksponents nosaka vesela skaitļa eksponenci un saknes ekstrakciju.

1. gadījums

Funkcijas $y=x^(a) $ eksponents ir naturāls skaitlis, tas ir, $y=x^(n) $, $n\in N$.

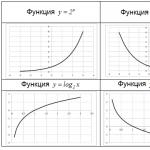
Ja $n=2\cdot k$ ir pāra skaitlis, tad funkcija $y=x^(2\cdot k) $ ir pāra un palielinās bezgalīgi tā, it kā arguments $\left(x\to +\infty \ right )$, un ar tā neierobežotu samazinājumu $\left(x\to -\infty \right)$. Šo funkcijas darbību var aprakstīt ar izteiksmēm $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k) =+\infty $ un $\mathop(\lim )\ limits_(x\to -\infty ) x^(2\cdot k) =+\infty $, kas nozīmē, ka funkcija abos gadījumos palielinās bez ierobežojumiem ($\lim $ ir ierobežojums). Piemērs: funkcijas $y=x^(2) $ grafiks.

Ja $n=2\cdot k-1$ ir nepāra skaitlis, tad funkcija $y=x^(2\cdot k-1) $ ir nepāra, palielinās bezgalīgi, kad arguments palielinās bezgalīgi, un samazinās bezgalīgi, kad tas samazinās. uz nenoteiktu laiku. Šo funkcijas darbību var aprakstīt ar izteiksmēm $\mathop(\lim )\limits_(x\to +\infty ) x^(2\cdot k-1) =+\infty $ un $\mathop(\lim )\limits_(x \to -\infty ) x^(2\cdot k-1) =-\infty $. Piemērs: funkcijas $y=x^(3) $ grafiks.

2. gadījums

Funkcijas $y=x^(a) $ eksponents ir negatīvs vesels skaitlis, tas ir, $y=\frac(1)(x^(n) ) $, $n\in N$.

Ja $n=2\cdot k$ ir pāra skaitlis, tad funkcija $y=\frac(1)(x^(2\cdot k) ) $ ir pāra un asimptotiski (pamazām) tuvojas nullei, tāpat kā ar neierobežotu pieauguma argumentu. , un ar tās neierobežotu samazināšanos. Šo funkcijas darbību var aprakstīt ar vienu izteiksmi $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k) ) =0$, kas nozīmē, ka ar neierobežotu argumenta pieaugumu absolūtajā vērtībā, funkcijas robeža ir nulle. Turklāt, tā kā argumentam ir tendence uz nulli gan kreisajā pusē $\left(x\to 0-0\right)$, gan labajā $\left(x\to 0+0\right)$, funkcija palielinās bez ierobežojums. Tāpēc izteiksmes $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x^(2\cdot k) ) =+\infty $ un $\mathop(\lim )\ limiti_ ir derīgi (x\līdz 0+0) \frac(1)(x^(2\cdot k) ) =+\infty $, kas nozīmē, ka funkcija $y=\frac(1)(x^(2) \cdot k ) ) $ abos gadījumos ir bezgalīgs ierobežojums, kas vienāds ar $+\infty $. Piemērs: funkcijas $y=\frac(1)(x^(2) ) $ grafiks.

Ja $n=2\cdot k-1$ ir nepāra skaitlis, tad funkcija $y=\frac(1)(x^(2\cdot k-1) ) $ ir nepāra un asimptotiski tuvojas nullei, it kā abas arguments pieaug un kad tas samazinās bez ierobežojumiem. Šo funkcijas darbību var aprakstīt ar vienu izteiksmi $\mathop(\lim )\limits_(x\to \infty ) \frac(1)(x^(2\cdot k-1) ) =0$. Turklāt, argumentam tuvojoties nullei kreisajā pusē, funkcija samazinās bez ierobežojumiem, un, kad arguments labajā pusē tuvojas nullei, funkcija palielinās bez ierobežojumiem, tas ir, $\mathop(\lim )\limits_(x\to 0-0) \frac(1)(x ^(2\cdot k-1) ) =-\infty $ un $\mathop(\lim )\limits_(x\to 0+0) \frac(1)( x^(2\cdot k-1) ) =+\infty $. Piemērs: funkcijas $y=\frac(1)(x) $ grafiks.

3. gadījums

Funkcijas $y=x^(a) $ eksponents ir naturālā skaitļa apgrieztā vērtība, tas ir, $y=\sqrt[(n)](x) $, $n\in N$.

Ja $n=2\cdot k$ ir pāra skaitlis, tad funkcijai $y=\pm \sqrt[(2\cdot k)](x) $ ir divas vērtības un tā ir definēta tikai $x\ge 0 $. Ar neierobežotu argumenta pieaugumu funkcijas $y=+\sqrt[(2\cdot k)](x) $ vērtība neierobežoti palielinās, bet funkcijas $y=-\sqrt[(2\) cdot k)](x) $ samazinās neierobežoti , tas ir, $\mathop(\lim )\limits_(x\to +\infty ) \left(+\sqrt[(2\cdot k)](x) \right )=+\infty $ un $\mathop( \lim )\limits_(x\to +\infty ) \left(-\sqrt[(2\cdot k)](x) \right)=-\infty $. Piemērs: funkcijas $y=\pm \sqrt(x) $ grafiks.

Ja $n=2\cdot k-1$ ir nepāra skaitlis, tad funkcija $y=\sqrt[(2\cdot k-1)](x) $ ir nepāra, palielinās neierobežoti ar neierobežotu argumenta pieaugumu. un samazinās neierobežoti, ja ir neierobežots, tas samazinās, tas ir, $\mathop(\lim )\limits_(x\to +\infty ) \sqrt[(2\cdot k-1)](x) =+\infty $ un $\mathop(\ lim )\limits_(x\to -\infty ) \sqrt[(2\cdot k-1)](x) =-\infty $. Piemērs: funkcijas $y=\sqrt[(3)](x) $ grafiks.

Eksponenciālās un logaritmiskās funkcijas

Eksponenciālās $y=a^(x) $ un logaritmiskās $y=\log _(a) x$ funkcijas ir savstarpēji apgrieztas. To grafiki ir simetriski attiecībā pret pirmā un trešā koordinātu leņķa kopējo bisektrisi.

Kad arguments $\left(x\to +\infty \right)$ palielinās bezgalīgi, eksponenciālā funkcija jeb $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =+\infty $ palielinās bezgalīgi, ja $a>1$ vai asimptotiski tuvojas nullei $\mathop(\lim )\limits_(x\to +\infty ) a^(x) =0$, ja $a1$ vai $\mathop palielinās bez ierobežojuma (\lim )\limits_(x\to -\infty ) a^(x) =+\infty $, ja $a

Funkcijas $y=a^(x) $ raksturīgā vērtība ir vērtība $x=0$. Šajā gadījumā visas eksponenciālās funkcijas neatkarīgi no $a$ noteikti krustojas ar $Oy$ asi pie $y=1$. Piemēri: funkciju $y=2^(x) $ un $y = \left (\frac(1)(2) \right)^(x) $ grafiki.

Logaritmiskā funkcija $y=\log _(a) x$ ir definēta tikai $x > 0$.

Tā kā arguments $\left(x\to +\infty \right)$ palielinās bezgalīgi, logaritmiskā funkcija vai $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=+ \ bezgalīgi palielinās infty $, ja $a>1$, vai bez ierobežojumiem samazinās $\mathop(\lim )\limits_(x\to +\infty ) \log _(a) x=-\infty $, ja $a1 $, vai bez ierobežojuma $\mathop(\lim )\limits_(x\to 0+0) \log _(a) x=+\infty $ palielinās, ja $a

Funkcijas $y=\log _(a) x$ raksturīgā vērtība ir vērtība $y=0$. Šajā gadījumā visas logaritmiskās funkcijas neatkarīgi no $a$ noteikti krustojas ar $Ox$ asi pie $x=1$. Piemēri: funkciju $y=\log _(2) x$ un $y=\log _(1/2) x$ grafiki.

Dažām logaritmiskajām funkcijām ir īpašs apzīmējums. Konkrēti, ja logaritma bāze ir $a=10$, tad šādu logaritmu sauc par decimāldaļu, un atbilstošo funkciju raksta kā $y=\lg x$. Un, ja par logaritma bāzi ir izvēlēts iracionālais skaitlis $e=2,7182818\ldots $, tad šādu logaritmu sauc par naturālu, un atbilstošo funkciju raksta kā $y=\ln x$. Tās apgrieztā vērtība ir funkcija $y=e^(x) $, ko sauc par eksponentu.

Pamata elementāras funkcijas ir: konstanta funkcija (konstante), sakne n-th pakāpe, jaudas funkcija, eksponenciālā, logaritmiskā funkcija, trigonometriskās un apgrieztās trigonometriskās funkcijas.

Pastāvīga funkcija.

Visu reālo skaitļu kopai konstanta funkcija tiek dota pēc formulas , kur C- kāds reāls skaitlis. Pastāvīga funkcija piešķir katru neatkarīgā mainīgā faktisko vērtību x tāda pati atkarīgā mainīgā vērtība y- nozīme AR. Pastāvīgu funkciju sauc arī par konstanti.

Pastāvīgas funkcijas grafiks ir taisna līnija, kas ir paralēla x asij un iet caur punktu ar koordinātām (0,C). Piemēram, parādīsim konstantu funkciju grafikus y=5,y=-2 un , kas attēlā zemāk atbilst attiecīgi melnajām, sarkanajām un zilajām līnijām.

Pastāvīgas funkcijas īpašības.

Domēns: visa reālo skaitļu kopa.

Pastāvīgā funkcija ir vienmērīga.

Vērtību diapazons: kopa, kas sastāv no vienskaitļa skaitļa AR.

Pastāvīga funkcija nepalielinās un nesamazinās (tāpēc tā ir nemainīga).

Nav jēgas runāt par konstantes izliekumu un ieliekumu.

Nav asimptotu.

Funkcija iet caur punktu (0,C) koordinātu plakne.

N-tās pakāpes sakne.

Apskatīsim elementāro pamatfunkciju, ko dod formula, kur n– naturāls skaitlis, kas lielāks par vienu.

N-tā sakne, n ir pāra skaitlis.

Sāksim ar saknes funkciju n-th jauda saknes eksponenta pāra vērtībām n.

Piemēram, šeit ir attēls ar funkciju grafiku attēliem un , tie atbilst melnām, sarkanām un zilām līnijām.

Pāra pakāpes saknes funkciju grafikiem ir līdzīgs izskats citām eksponenta vērtībām.

Saknes funkcijas īpašībasn -th jauda patn .

N-tā sakne n ir nepāra skaitlis.

Saknes funkcija n-th jauda ar nepāra saknes eksponentu n ir definēts uz visu reālo skaitļu kopu. Piemēram, šeit ir funkciju grafiki un , tie atbilst melnajām, sarkanajām un zilajām līknēm.

1) Funkciju domēns un funkciju domēns.

Funkcijas domēns ir visu derīgo derīgo argumentu vērtību kopa x(mainīgs x), kurai funkcija y = f(x) noteikts. Funkcijas diapazons ir visu reālo vērtību kopa y, ko funkcija pieņem.

Elementārajā matemātikā funkcijas tiek pētītas tikai uz reālo skaitļu kopas.

2) Funkcijas nulles.

Funkcija nulle ir argumenta vērtība, pie kuras funkcijas vērtība ir vienāda ar nulli.

3) Funkcijas pastāvīgās zīmes intervāli.

Funkcijas pastāvīgās zīmes intervāli ir argumentu vērtību kopas, kurās funkcijas vērtības ir tikai pozitīvas vai tikai negatīvas.

4) Funkcijas monotonitāte.

Palielinoša funkcija (noteiktā intervālā) ir funkcija, kurā lielāka argumenta vērtība no šī intervāla atbilst lielākai funkcijas vērtībai.

Samazinoša funkcija (noteiktā intervālā) ir funkcija, kurā lielāka argumenta vērtība no šī intervāla atbilst mazākai funkcijas vērtībai.

5) Pāra (nepāra) funkcija.

Pāra funkcija ir funkcija, kuras definīcijas apgabals ir simetrisks attiecībā pret izcelsmi un jebkurai X no definīcijas jomas vienlīdzība f(-x) = f(x). Pāra funkcijas grafiks ir simetrisks attiecībā pret ordinātu.

Nepāra funkcija ir funkcija, kuras definīcijas apgabals ir simetrisks attiecībā pret izcelsmi un jebkurai X no definīcijas jomas vienlīdzība ir patiesa f(-x) = - f(x). Nepāra funkcijas grafiks ir simetrisks attiecībā pret izcelsmi.

6) Ierobežotas un neierobežotas funkcijas.

Funkciju sauc par ierobežotu, ja ir tāds pozitīvs skaitlis M, ka |f(x)| ≤ M visām x vērtībām. Ja šāda numura nav, tad funkcija ir neierobežota.

7) Funkcijas periodiskums.

Funkcija f(x) ir periodiska, ja ir skaitlis T, kas atšķiras no nulles, un jebkuram x no funkcijas definīcijas domēna ir spēkā sekojošais: f(x+T) = f(x). Šo mazāko skaitli sauc par funkcijas periodu. Visas trigonometriskās funkcijas ir periodiskas. (Trigonometriskās formulas).

19. Pamatelementāras funkcijas, to īpašības un grafiki. Funkciju pielietojums ekonomikā.

Pamata elementāras funkcijas. To īpašības un grafiki

1. Lineārā funkcija.

Lineāra funkcija sauc par formas funkciju, kur x ir mainīgais, a un b ir reāli skaitļi.

Numurs A ko sauc par līnijas slīpumu, tas ir vienāds ar šīs līnijas slīpuma leņķa pieskari x ass pozitīvajam virzienam. Lineāras funkcijas grafiks ir taisna līnija. To nosaka divi punkti.

Lineāras funkcijas īpašības

1. Definīcijas joma - visu reālo skaitļu kopa: D(y)=R

2. Vērtību kopa ir visu reālo skaitļu kopa: E(y)=R

3. Funkcija iegūst nulles vērtību, kad vai.

4. Funkcija palielinās (samazinās) visā definīcijas jomā.

5. Lineāra funkcija ir nepārtraukta visā definīcijas jomā, diferencējama un .

2. Kvadrātfunkcija.

Formas funkciju, kur x ir mainīgais, koeficienti a, b, c ir reāli skaitļi, sauc kvadrātveida.

Ņemot vērā sarežģītā mainīgā funkcijas, Liouville definēja elementārās funkcijas nedaudz plašāk. Elementāra funkcija y mainīgs x- analītiskā funkcija, ko var attēlot kā algebrisku funkciju x un funkcijas , un ir kādas algebriskas funkcijas logaritms vai eksponents g 1 no x .

Piemēram, grēks ( x) - algebriskā funkcija e ix .

Neierobežojot apsvēruma vispārīgumu, mēs varam uzskatīt funkcijas par algebriski neatkarīgām, tas ir, ja algebriskais vienādojums ir izpildīts visiem x, tad visi polinoma koeficienti ir vienādi ar nulli.

Elementāro funkciju diferenciācija

Kur z 1 "(z) ir vienāds ar vai g 1 " / g 1 vai z 1 g 1" atkarībā no tā, vai tas ir logaritms z 1 vai eksponenciāls utt. Praksē ir ērti izmantot atvasinājumu tabulu.

Elementāro funkciju integrēšana

Liuvila teorēma ir pamats elementāru funkciju simboliskās integrācijas algoritmu izveidei, kas realizēti, piemēram,

Limitu aprēķins

Liouville teorija neattiecas uz ierobežojumu aprēķināšanu. Nav zināms, vai pastāv algoritms, kas, ņemot vērā elementārās formulas doto secību, dod atbildi, vai tai ir ierobežojums vai nav. Piemēram, ir atklāts jautājums, vai secība saplūst.

Literatūra

• J. Liuvils. Mémoire sur l'intégration d'une classe de fonctions transcendantes// J. Reine Anžē. Matemātika. Bd. 13. lpp. 93-118. (1835)
• J.F. Ritt. Integrācija ierobežotos noteikumos. N.-Y., 1949 // http://lib.homelinux.org
• A. G. Khovanskis. Topoloģiskā Galois teorija: vienādojumu atrisināmība un neatrisināmība galīgā formā Ch. 1. M, 2007. gads

Piezīmes

Wikimedia fonds. 2010. gads.

• Elementāra uzbudināšana
• Elementārs iznākums

Skatiet, kas ir “elementārā funkcija” citās vārdnīcās:

elementāra funkcija- Funkcija, kuru, sadalot mazākās funkcijās, nevar unikāli definēt digitālās pārraides hierarhijā. Tāpēc no tīkla viedokļa tas ir nedalāms (ITU T G.806). Tēmas: telekomunikācijas, pamatjēdzieni EN adaptācijas funkcijaA... Tehniskā tulkotāja rokasgrāmata

mijiedarbības funkcija starp tīkla līmeņiem- elementāra funkcija, kas nodrošina raksturīgās informācijas mijiedarbību starp diviem tīkla slāņiem. (ITU T G.806). Tēmas: telekomunikācijas, EN slāņa pamatjēdzieni... ... Tehniskā tulkotāja rokasgrāmata