Kā atrisināt sudoku veidus. Loģiskās mīklas

• pamācība

1. Pamati

Lielākā daļa no mums, hakeriem, zina, kas ir sudoku. Es nerunāšu par noteikumiem, bet nekavējoties pārietu pie metodēm.
Lai atrisinātu mīklu, neatkarīgi no tā, cik sarežģīta vai vienkārša, sākotnēji tiek meklētas šūnas, kuras ir acīmredzami jāaizpilda.

1.1 "Pēdējais varonis"

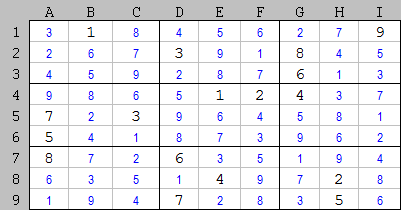
Apsveriet septīto kvadrātu. Tikai četras brīvas šūnas, lai kaut ko varētu ātri aizpildīt.
"8 " uz D3 bloku polsterējums H3 un J3; līdzīgi" 8 " uz G5 aizveras G1 un G2
Ar tīru sirdsapziņu mēs liekam " 8 " uz H1

1.2 "Pēdējais varonis" pēc kārtas

Kad esat apskatījis kvadrātus, lai atrastu acīmredzamus risinājumus, pārejiet uz kolonnām un rindām.
Apsveriet " 4 " laukumā. Skaidrs, ka tas būs kaut kur ierindā A .
Mums ir " 4 " uz G3 kas aptver A3, tur ir " 4 " uz F7, tīrīšana A7. Un vēl vienu" 4 " Otrajā laukumā aizliedz tā atkārtošanu A4 un A6.
"Pēdējais varonis" mūsu " 4 "Šo A2

1.3 “Nav izvēles”

Dažreiz tam ir vairāki iemesli konkrēta vieta. "4 " iekšā J8 būtu lielisks piemērs.
Zils bultiņas norāda, ka šis ir pēdējais iespējamais skaitlis kvadrātā. sarkans un zils bultiņas dod mums pēdējo numuru kolonnā 8 . Zaļumi bultiņas norāda pēdējo iespējamo numuru rindā Dž.
Kā redzat, mums nav citas izvēles kā ievietot šo " 4 "vietā.

1.4 "Un kurš, ja ne es?"

Ciparu aizpildīšanu ir vieglāk izdarīt, izmantojot iepriekš aprakstītās metodes. Tomēr, pārbaudot skaitli kā pēdējo iespējamo vērtību, tiek iegūti arī rezultāti. Metode jāizmanto, kad šķiet, ka visi cipari ir, bet kaut kā pietrūkst.
"5 " iekšā B1 ir iestatīts, pamatojoties uz faktu, ka visi skaitļi no " 1 "pirms" 9 ", Turklāt " 5 " atrodas rindā, kolonnā un kvadrātā (atzīmēts zaļā krāsā).

Žargonā tas ir " kails vientuļnieks". Ja aizpildīsiet lauku ar iespējamām vērtībām​​(kandidāti), tad šūnā šāds skaitlis būs vienīgais iespējamais. Izstrādājot šo paņēmienu, varat meklēt " slēptie vientuļnieki" - skaitļi, kas ir unikāli konkrētai rindai, kolonnai vai kvadrātam.

2. "Kailā jūdze"

2.1 Kaili pāri

""Kails" pāris" - divu kandidātu kopa, kas atrodas divās šūnās, kas pieder vienam kopējam blokam: rinda, kolonna, kvadrāts.
Ir skaidrs ka pareizos lēmumus mīklas būs tikai šajās šūnās un tikai ar šīm vērtībām, savukārt visus pārējos kandidātus no vispārējā bloka var noņemt.


Šajā piemērā ir vairāki "kaili pāri".
sarkans rindā BETšūnas ir izceltas A2 un A3, abi satur " 1 " un " 6 ". Pagaidām precīzi nezinu, kā tie šeit atrodas, bet visus pārējos varu droši noņemt" 1 " un " 6 "no virknes A(atzīmēts dzeltenā krāsā). Arī A2 un A3 pieder pie kopējā laukuma, tāpēc mēs noņemam " 1 "no C1.

2.2 "Trīsnieks"

"Kaili trijnieki"- sarežģīta "kailu pāru" versija.
Jebkura trīs šūnu grupa vienā blokā, kas satur visā visumā ir trīs kandidāti "kails trio". Kad šāda grupa tiek atrasta, šos trīs kandidātus var noņemt no citām bloka šūnām.

Kandidātu kombinācijas priekš "kails trio" var būt šādi:

// trīs skaitļi trīs šūnās.
// jebkuras kombinācijas.
// jebkuras kombinācijas.

Šajā piemērā viss ir diezgan skaidrs. Šūnas piektajā kvadrātā E4, E5, E6 satur [ 5,8,9 ], [5,8 ], [5,9 ]. Izrādās, ka kopumā šīm trim šūnām ir [ 5,8,9 ], un tur var būt tikai šie skaitļi. Tas ļauj mums tos noņemt no citiem bloķēšanas kandidātiem. Šis triks sniedz mums risinājumu " 3 "šūnai E7.

2.3 "Fab Four"

"Kailais četrinieks"ļoti reta lieta, īpaši iekšā pilna forma, un joprojām rada rezultātus, kad tie tiek atrasti. Risinājuma loģika ir tāda pati kā "kaili trīnīši".

Iepriekš minētajā piemērā šūnas pirmajā kvadrātā A1, B1, B2 un C1 parasti satur [ 1,5,6,8 ], tāpēc šie skaitļi aizņems tikai šīs šūnas, nevis citas. Mēs noņemam dzeltenā krāsā iezīmētos kandidātus.

3. "Viss apslēptais kļūst skaidrs"

3.1 Slēptie pāri

Lielisks veids, kā atvērt lauku, ir meklēt slēptie pāri. Šī metode ļauj noņemt no šūnas nevajadzīgos kandidātus un radīt interesantākas stratēģijas.

Šajā mīklā mēs to redzam 6 un 7 atrodas pirmajā un otrajā lauciņā. Turklāt 6 un 7 atrodas kolonnā 7 . Apvienojot šos nosacījumus, mēs varam apgalvot, ka šūnās A8 un A9 būs tikai šīs vērtības, un mēs noņemam visus pārējos kandidātus.


Interesantāks un sarežģītāks piemērs slēptie pāri. Pāris [ 2,4 ] iekšā D3 un E3, tīrīšana 3 , 5 , 6 , 7 no šīm šūnām. Sarkanā krāsā iezīmēti divi slēpti pāri, kas sastāv no [ 3,7 ]. No vienas puses, tie ir unikāli divām šūnām 7 kolonnu, no otras puses - rindai E. Dzeltenā krāsā iezīmētie kandidāti tiek noņemti.

3.1 Slēptie trīnīši

Mēs varam attīstīties slēptie pāri pirms tam slēptie trīnīši vai pat slēptie četrinieki. Apslēptais trīs sastāv no trim skaitļu pāriem, kas atrodas vienā blokā. Piemēram, un. Tomēr, tāpat kā gadījumā ar "kaili trīnīši", katrā no trim šūnām nav jāsatur trīs skaitļi. strādās Kopā trīs skaitļi trīs šūnās. Piemēram , , . Slēptie trīnīši tiks maskēti no citiem kandidātiem kamerās, tāpēc vispirms jums par to jāpārliecinās trijotne attiecas uz konkrētu bloku.


Tajā sarežģīts piemērs ir divi slēptie trīnīši. Pirmais, kas atzīmēts ar sarkanu, kolonnā BET. Šūna A4 satur [ 2,5,6 ], A7 - [2,6 ] un šūna A9 -[2,5 ]. Šīs trīs šūnas ir vienīgās, kurās var būt 2, 5 vai 6, tāpēc tās būs vienīgās. Tāpēc mēs noņemam nevajadzīgos kandidātus.

Otrkārt, kolonnā 9 . [4,7,8 ] ir unikālas šūnām B9, C9 un F9. Izmantojot to pašu loģiku, mēs noņemam kandidātus.

3.1 Slēptie četrinieki

Ideāls piemērs slēptie četrinieki. [1,4,6,9 ] piektajā kvadrātā var būt tikai četrās šūnās D4, D6, F4, F6. Sekojot mūsu loģikai, mēs noņemam visus pārējos kandidātus (atzīmēti ar dzeltenu).

4. "bez gumijas"

Ja kāds no cipariem parādās divreiz vai trīsreiz vienā blokā (rindā, kolonnā, kvadrātā), mēs varam noņemt šo skaitli no konjugāta bloka. Ir četri savienošanas pārī veidi:

1. Pāris vai Trīs kvadrātā - ja tie atrodas vienā rindā, tad visas pārējās līdzīgās vērtības varat noņemt no atbilstošās rindas.
2. Pāris vai Trīs kvadrātā - ja tie atrodas vienā kolonnā, tad visas pārējās līdzīgās vērtības varat noņemt no attiecīgās kolonnas.
3. Pāris vai Trīs pēc kārtas – ja tie atrodas vienā un tajā pašā laukumā, tad visas pārējās līdzīgās vērtības var noņemt no attiecīgā kvadrāta.
4. Pāris vai Trīs kolonnā - ja tie atrodas vienā kvadrātā, tad visas pārējās līdzīgās vērtības varat noņemt no attiecīgā kvadrāta.

4.1 Rādītāju pāri, trīskārši

Ļaujiet man parādīt jums šo mīklu kā piemēru. Trešajā laukumā 3 "ir tikai iekšā B7 un B9. Pēc paziņojuma №1 , mēs noņemam kandidātus no B1, B2, B3. Tāpat, " 2 " noņem no astotā laukuma iespējamā nozīme no G2.


Īpaša mīkla. Ļoti grūti atrisināt, bet, ja paskatās uzmanīgi, jūs varat redzēt dažus rādītāju pāri. Skaidrs, ka ne vienmēr tie visi ir jāatrod, lai virzītos uz priekšu risinājumā, taču katrs šāds atradums atvieglo mūsu uzdevumu.

4.2. Nereducējamā samazināšana

Šī stratēģija ietver rūpīgu rindu un kolonnu parsēšanu un salīdzināšanu ar kvadrātu saturu (noteikumi №3 , №4 ).
Apsveriet līniju BET. "2 "ir iespējamas tikai A4 un A5. ievērojot noteikumu №3 , noņemt " 2 "viņiem B5, C4, C5.


Turpināsim risināt mīklu. Mums ir viena vieta 4 "viena kvadrātcollas rādiusā 8 kolonna. Saskaņā ar noteikumu №4 , mēs noņemam nevajadzīgos kandidātus un papildus iegūstam risinājumu " 2 " priekš C7.

Pirmā lieta, kas būtu jānosaka problēmu risināšanas metodoloģijā, ir jautājums par reālu izpratni par to, ko mēs sasniedzam un varam sasniegt problēmu risināšanas ziņā. Sapratne parasti tiek uzskatīta par kaut ko pašsaprotamu, un mēs aizmirstam par to, ka izpratnei ir noteikts izpratnes sākumpunkts, tikai attiecībā uz kuru mēs varam teikt, ka izpratne patiešām notiek no konkrēta mūsu noteikta brīža. Sudoku šeit, mūsuprāt, ir ērts ar to, ka tas, izmantojot savu piemēru, ļauj zināmā mērā modelēt problēmu izpratnes un risināšanas jautājumus. Tomēr sāksim ar vairākiem citiem un ne mazāk svarīgiem piemēriem kā Sudoku.

Fiziķis, kurš pēta īpašo relativitāti, varētu runāt par Einšteina "kristāldzidrajiem" priekšlikumiem. Es uzgāju šo frāzi vienā no interneta vietnēm. Bet kur sākas šī "kristāla skaidrības" izpratne? Tas sākas ar mācīšanos matemātiskais apzīmējums postulāti, no kuriem pēc zināmiem un saprotamiem noteikumiem var uzbūvēt visas SRT daudzstāvu matemātiskās konstrukcijas. Bet tas, ko fiziķis, tāpat kā es, nesaprot, kāpēc SRT postulāti darbojas tā, nevis citādi.

Pirmkārt, lielais vairums šo doktrīnu apspriežošo nesaprot, kas īsti slēpjas postulātā par gaismas ātruma nemainīgumu tulkojumā no tā matemātiskā pielietojuma uz realitāti. Un šis postulāts nozīmē gaismas ātruma nemainīgumu visās iedomājamās un neiedomājamās nozīmēs. Gaismas ātrums ir nemainīgs attiecībā pret jebkuriem vienlaicīgi atpūšošiem un kustīgiem objektiem. Gaismas stara ātrums saskaņā ar postulātu ir nemainīgs pat attiecībā pret pretimnākošo, šķērsvirziena un attālināto gaismas staru. Un tajā pašā laikā mums ir tikai tādi mērījumi, kas ir netieši saistīti ar gaismas ātrumu, kas tiek interpretēts kā tā noturība.

Ņūtona likumi fiziķim un pat tiem, kas vienkārši studē fiziku, ir tik pazīstami, ka šķiet tik saprotami kā kaut kas pašsaprotams, un citādi nevar būt. Bet teiksim likuma piemērošanu smagums sākas ar tā matemātisko apzīmējumu, pēc kura var aprēķināt pat kosmosa objektu trajektorijas un orbītu raksturlielumus. Bet kāpēc šie likumi darbojas tā un ne citādi - tādas izpratnes mums nav.

Tāpat ar Sudoku. Internetā jūs varat atrast vairākkārt atkārtotus aprakstus par "pamata" veidiem, kā atrisināt Sudoku problēmas. Ja atceraties šos noteikumus, varat saprast, kā šī vai cita Sudoku problēma tiek atrisināta, piemērojot "pamata" noteikumus. Bet man ir jautājums: vai mēs saprotam, kāpēc šīs "pamata" metodes darbojas tā, nevis citādi.

Tāpēc mēs pārejam pie nākamā atslēgas pozīcija problēmu risināšanas metodoloģijā. Izpratne ir iespējama tikai pamatojoties uz kādu modeli, kas dod pamatu šai izpratnei un spējai veikt kādu dabisku vai domu eksperimentu. Bez tā mums var būt tikai noteikumi apgūto sākumpunktu piemērošanai: SRT postulāti, Ņūtona likumi vai Sudoku "pamata" veidi.

Mums nav un principā nevar būt modeļu, kas atbilstu gaismas ātruma neierobežotās konstantes postulātam. Mēs to nedarām, taču var izgudrot nepierādāmus modeļus, kas atbilst Ņūtona likumiem. Un ir tādi "Ņūtona" modeļi, bet tie kaut kā nepārsteidz ar produktīvām iespējām veikt pilna mēroga vai domu eksperimentu. Taču Sudoku sniedz mums iespējas, ko varam izmantot, lai izprastu faktiskās Sudoku problēmas un ilustrētu modelēšanu kā vispārēju pieeju problēmu risināšanai.

Viens no iespējamiem Sudoku problēmu modeļiem ir darblapa. Tas tiek izveidots, vienkārši aizpildot visas uzdevumā norādītās tabulas tukšās šūnas (šūnas) ar cipariem 123456789. Pēc tam uzdevums tiek reducēts līdz visu lieko ciparu secīgai izņemšanai no šūnām, līdz tiek aizpildītas visas tabulas šūnas. aizpildīts ar atsevišķiem (ekskluzīviem) cipariem, kas apmierina problēmas nosacījumu.

Es veidoju šādu darblapu programmā Excel. Pirmkārt, es atlasu visas tukšās tabulas šūnas (šūnas). Nospiežu F5-"Atlasīt"-"Tukšas šūnas"-"Labi". Vispārīgāks veids, kā atlasīt vēlamās šūnas: turiet nospiestu taustiņu Ctrl un noklikšķiniet ar peli, lai atlasītu šīs šūnas. Pēc tam atlasītajām šūnām es iestatīju zila krāsa, izmērs 10 (oriģināls - 12) un fonts Arial Narrow. Tas viss, lai turpmākās izmaiņas tabulā būtu skaidri redzamas. Tālāk es ieeju tukšas šūnas numuri 123456789. Daru šādi: pierakstu un saglabāju šo numuru atsevišķā šūnā. Tad es nospiežu F2, atlasu un nokopēju šo numuru ar Ctrl + C darbību. Tālāk es dodos uz tabulas šūnām un, secīgi apejot visas tukšās šūnas, ievadu tajās numuru 123456789, izmantojot darbību Ctrl + V, un darblapa ir gatava.

Papildu numurus, kas tiks apspriesti vēlāk, es svītroju šādi. Ar operāciju Ctrl + peles klikšķis - es atlasu šūnas ar papildu numuru. Tad es nospiežu Ctrl + H un atveramā loga augšējā laukā ievadu dzēšamo numuru, un apakšējam laukam jābūt pilnīgi tukšam. Pēc tam atliek noklikšķināt uz opcijas "Aizstāt visu", un papildu numurs tiek noņemts.

Spriežot pēc tā, ka man ierastajos "pamata" veidos parasti izdodas veikt progresīvāku tabulu apstrādi nekā internetā sniegtajos piemēros, tad darblapa ir visvairāk vienkāršs rīks Sudoku problēmu risināšanā. Turklāt daudzas situācijas saistībā ar sarežģītāko tā saukto "pamata" noteikumu piemērošanu manā darblapā vienkārši neradās.

Tajā pašā laikā darblapa ir arī modelis, uz kura var veikt eksperimentus, pēc tam identificējot visus "pamata" noteikumus un dažādas to piemērošanas nianses, kas izriet no eksperimentiem.

Tātad, pirms jums ir darblapas fragments ar deviņiem blokiem, kas numurēti no kreisās puses uz labo un no augšas uz leju. Šajā gadījumā mums ir ceturtais bloks, kas aizpildīts ar numuriem 123456789. Šis ir mūsu modelis. Ārpus bloka mēs sarkanā krāsā iezīmējām "aktivizētos" (galīgi definētos) skaitļus, šajā gadījumā četriniekus, kurus mēs plānojam aizstāt veidojamajā tabulā. Zilie piecinieki ir skaitļi, kas vēl nav noteikti attiecībā uz viņu turpmāko lomu, par ko mēs runāsim vēlāk. Mūsu piešķirtie aktivizētie cipari it kā izsvītro, izstumj, dzēš - kopumā tie blokā izspiež vienus un tos pašus ciparus, tātad tur ir attēloti bālā krāsā, simbolizējot to, ka šie bālie cipari ir bijuši dzēsts. Gribējās šo krāsu padarīt vēl bālāku, bet tad tās varētu kļūt pavisam neredzamas, skatoties internetā.

Rezultātā ceturtajā blokā, šūnā E5, bija viens, arī aktivizēts, bet paslēpts četri. "Aktivizēta", jo viņa, savukārt, var arī noņemt papildu ciparus, ja tie ir ceļā, un "paslēpta", jo viņa ir starp citiem cipariem. Ja šūnai E5 uzbrūk pārējie, izņemot 4, aktivizētie numuri 12356789, tad E5 parādīsies "pliks" vientuļnieks - 4.

Tagad noņemsim vienu aktivizēto četrinieku, piemēram, no F7. Tad četrinieks aizpildītajā blokā var būt jau un tikai šūnā E5 vai F5, paliekot aktivizēts 5. rindā. Ja šajā situācijā ir iesaistīti aktivizētie piecinieki, bez F7=4 un F8=5, tad šūnās E5 un F5 tur ir. būs pliks vai slēpts aktivizēts pāris 45.

Pēc tam, kad esat pietiekami izstrādājis un sapratis dažādi varianti ar plikiem un slēptiem vientuļiem, divniekiem, trijiem utt. ne tikai blokos, bet arī rindās un kolonnās varam pāriet uz citu eksperimentu. Izveidosim tukšu pāri 45, kā to darījām iepriekš, un tad savienosim aktivizētos F7=4 un F8=5. Rezultātā izveidosies situācija E5=45. Līdzīgas situācijas ļoti bieži rodas darba lapas apstrādes procesā. Šī situācija nozīmē, ka vienam no šiem cipariem, šajā gadījumā 4 vai 5, obligāti jābūt blokā, rindā un kolonnā, kas ietver šūnu E5, jo visos šajos gadījumos ir jābūt diviem cipariem, nevis vienam no tiem.

Un pats galvenais, mēs jau zinām, cik bieži rodas situācijas, piemēram, E5=45. Līdzīgā veidā mēs definēsim situācijas, kad vienā šūnā parādās ciparu trīskāršs utt. Un, kad mēs novedam šo situāciju izpratnes un uztveres pakāpi līdz pašsaprotamības un vienkāršības stāvoklim, tad nākamais solis ir, tā sakot, situāciju zinātniska izpratne: tad mēs varēsim veikt statistisku analīzi par šīm situācijām. Sudoku tabulas, identificējiet modeļus un izmantojiet uzkrāto materiālu, lai atrisinātu visvairāk grūtākie uzdevumi.

Tādējādi, eksperimentējot ar modeli, mēs iegūstam vizuālu un pat "zinātnisku" slēptu vai atvērtu singlu, pāru, trīskāršu utt. Ja aprobežojaties ar darbībām ar aprakstīto vienkāršo modeli, dažas jūsu idejas izrādīsies neprecīzas vai pat kļūdainas. Tomēr, kad esat nonācis pie risinājuma konkrēti uzdevumi, tad sākotnējo ideju neprecizitātes ātri vien nāks gaismā, bet modeļi, uz kuriem tika veikti eksperimenti, būs jāpārdomā un jāpilnveido. Tas ir neizbēgams hipotēžu un precizējumu ceļš jebkuru problēmu risināšanā.

Man jāsaka, ka slēptie un atvērtie singli, kā arī atvērtie pāri, trīskārši un pat četrinieki ir izplatītas situācijas, kas rodas, risinot Sudoku problēmas ar darblapu. Slēptie pāri bija reti. Un šeit ir slēptie trīskārši, četrinieki utt. Man kaut kā nesanāca apstrādājot darblapas, tāpat kā internetā vairākkārt aprakstītās “x-wing” un “zobenzivs” kontūru apiešanas metodes, kurās ir “kandidāti” dzēšanai ar kādu no divi alternatīvi kontūru apiešanas veidi. Šo metožu nozīme: ja iznīcinām "kandidātu" x1, tad ekskluzīvais kandidāts x2 paliek un tajā pašā laikā kandidāts x3 tiek dzēsts, un ja iznīcinām x2, tad paliek ekskluzīvais x1, bet šajā gadījumā kandidāts Arī x3 tiek dzēsts, tāpēc jebkurā gadījumā x3 ir jāsvītro , pagaidām neskarot kandidātus x1 un x2. Vairāk ģenerālplāns, Šis īpašs gadījums situācijas: ja divas alternatīvi veidi noved pie tā paša rezultāta, tad šo rezultātu var izmantot, lai atrisinātu Sudoku problēmu. Šajā, vispārīgākā, situācijā es sastapu situācijas, bet ne "x-wing" un "swordfish" variantos, un ne risinot Sudoku problēmas, kurām pietiek ar zināšanām tikai par "pamata" pieejām.

Darblapas izmantošanas iespējas var parādīt šajā netriviālajā piemērā. Vienā no sudoku risinātāju forumiem http://zforum.net/index.php?topic=3955.25;wap2 es saskāros ar problēmu, kas tika pasniegta kā viena no grūtākajām sudoku problēmām, kas nav atrisināma parastajos veidos, neizmantojot uzskaiti ar pieņēmumi par šūnās aizvietotajiem skaitļiem. Parādīsim, ka ar darba tabulu šo problēmu var atrisināt bez šāda uzskaitījuma:

Labajā pusē ir sākotnējais uzdevums, pa kreisi ir darba tabula pēc "dzēšanas", t.i. parastā papildu ciparu noņemšanas darbība.

Pirmkārt, vienosimies par apzīmējumu. ABC4=689 nozīmē, ka šūnās A4, B4 un C4 ir skaitļi 6, 8 un 9 — viens vai vairāki cipari katrā šūnā. Tāpat ir ar stīgām. Tādējādi B56=24 nozīmē, ka šūnās B5 un B6 ir skaitļi 2 un 4. Zīme ">" ir nosacījuma darbības zīme. Tādējādi D4=5>I4-37 nozīmē, ka ziņojuma D4=5 dēļ šūnā I4 jāievieto skaitlis 37. Vēstījums var būt izteikts – “kails” – un slēpts, kas būtu jāatklāj. Ziņojuma ietekme var būt secīga (pārraidīta netieši) pa ķēdi un paralēli (darboties tieši uz citām šūnām). Piemēram:

D3=2; D8=1>A9-1>A2-2>A3-4,G9-3; (D8=1)+(G9=3)>G8-7>G7-1>G5-5

Šis ieraksts nozīmē, ka D3=2, bet šis fakts ir jāatklāj. D8=1 nodod savu darbību uz ķēdi uz A3 un 4 jāraksta uz A3; tajā pašā laikā D3=2 iedarbojas tieši uz G9, kā rezultātā G9-3. (D8=1)+(G9=3)>G8-7 – faktoru (D8=1) un (G9=3) kopējā ietekme noved pie rezultāta G8-7. utt.

Ieraksti var ietvert arī H56/68 tipa kombināciju. Tas nozīmē, ka skaitļi 6 un 8 ir aizliegti šūnās H5 un H6, t.i. tie ir jāizņem no šīm šūnām.

Tātad, sākam strādāt ar tabulu un iesākumam piemērojam labi manifestēto, pamanāmo nosacījumu ABC4=689. Tas nozīmē, ka visās pārējās (izņemot A4, B4 un C4) 4. bloka šūnās (vidū, pa kreisi) un 4. rindā skaitļi 6, 8 un 9 ir jāsvītro:

Uzklājiet B56=24 tādā pašā veidā. Kopā mums ir D4=5 un (pēc D4=5>I4-37) HI4=37, kā arī (pēc B56=24>C6-1) C6=1. Piemērosim šo darblapai:

In I89=68slēpts>I56/68>H56-68: t.i. šūnās I8 un I9 ir slēpts 5. un 6. ciparu pāris, kas aizliedz šiem cipariem atrasties I56, kā rezultātā tiek iegūts rezultāts H56-68. Šo fragmentu varam aplūkot savādāk, tāpat kā to darījām eksperimentos ar darblapas modeli: (G23=68)+(AD7=68)>I89-68; (I89=68)+(ABC4=689)>H56-68. Tas ir, divvirzienu "uzbrukums" (G23=68) un (AD7=68) noved pie tā, ka I8 un I9 var atrasties tikai skaitļi 6 un 8. Tālāk (I89=68) ir savienots ar " uzbrukums" H56 kopā ar iepriekšējiem nosacījumiem, kas noved pie H56-68. Papildus šim "uzbrukumam" ir pieslēgts (ABC4=689), kas in šis piemērs izskatās lieki, bet, ja strādātu bez darblapas, tad ietekmes faktors (ABC4=689) būtu paslēpts, un tam būtu lietderīgi pievērst īpašu uzmanību.

Nākamā darbība: I5=2>G1-2,G6-9,B6-4,B5-2.

Es ceru, ka tas ir skaidrs jau bez komentāriem: aizstājiet ciparus, kas nāk aiz domuzīmes, jūs nevarat kļūdīties:

H7=9>I7-4; D6=8>D1-4,H6-6>H5-8:

Nākamā darbību sērija:

D3=2; D8=1>A9-1>A2-2>A3-4,G9-3;

(D8=1)+(G9=3)>G8-7>G7-1>G5-5;

D5=9>E5-6>F5-4:

I=4>C9-4>C7-2>E9-2>EF7-35>B7-7, F89-89,

tas ir, "izsvītrošanas" - papildu ciparu dzēšanas - rezultātā šūnās F8 un F9 parādās atvērts, "kails" pāris 89, ko kopā ar citiem ierakstā norādītajiem rezultātiem attiecinām uz tabulu:

H2=4>H3-1>F2-1>F1-6>A1-3>B8-3,C8-5,H1-7>I2-5>I3-3>I4-7>H4-3

Viņu rezultāts:

Tam seko diezgan ierastas, acīmredzamas darbības:

H1=7>C1-8>E1-5>F3-7>E2-9>E3-8,C3-9>B3-5>B2-6>C2-7>C4-6>A4-9>B4- astoņi;

B2=6>B9-9>A8-6>I8-8>F8-9>F9-8>I9-6;

E7=3>F7-5,E6-7>F6-3

Viņu rezultāts: problēmas galīgais risinājums:

Tā vai citādi mēs pieņemsim, ka mēs izdomājām "pamata" metodes Sudoku vai citās intelektuālās pielietošanas jomās, pamatojoties uz šim piemērotu modeli un pat iemācījāmies tās pielietot. Bet tā ir tikai daļa no mūsu progresa problēmu risināšanas metodoloģijā. Turklāt, es atkārtoju, tas ne vienmēr tiek ņemts vērā, bet gan neaizstājams posms iepriekš apgūto metožu nogādāšanai līdz to pielietošanas vienkāršībai. Atrisinot piemērus, izprotot šī risinājuma rezultātus un metodes, pārdomājot šo materiālu uz pieņemtā modeļa pamata, vēlreiz pārdomājot visus variantus, nogādājot to izpratnes pakāpi līdz automātiskumam, kad risinājums, izmantojot "pamata" nosacījumus, kļūst par rutīnu. un pazūd kā problēma. Ko tas dod: katram tas jājūt pēc savas pieredzes. Un būtība ir tāda, ka, problēmsituācijai kļūstot par rutīnu, intelekta meklēšanas mehānisms tiek virzīts uz arvien sarežģītāku noteikumu izstrādi risināmo problēmu jomā.

Un kas ir "sarežģītāki noteikumi"? Tie ir tikai jauni "pamata" nosacījumi problēmas risināšanā, kuru izpratni savukārt var novest arī līdz vienkāršības stāvoklim, ja tiek atrasts šim nolūkam piemērots modelis.

Rakstā Vasiļenko S.L. "Numeric Harmony Sudoku" Es atrodu problēmas piemēru ar 18 simetriskiem taustiņiem:

Attiecībā uz šo uzdevumu teikts, ka ar "pamata" metodēm to var atrisināt tikai līdz noteiktam stāvoklim, pēc kura sasniegšanas atliek tikai pielietot vienkāršu uzskaitījumu ar izmēģinājuma aizstāšanu dažu it kā ekskluzīvu (viena, vienota) šūnās. ) cipari. Šis stāvoklis (nedaudz tālāk nekā Vasiļenko piemērā) izskatās šādi:

Ir tāds modelis. Tas ir sava veida rotācijas mehānisms identificētiem un neidentificētiem ekskluzīviem (vieniem) cipariem. Vienkāršākajā gadījumā daži ekskluzīvu ciparu trīskārši griežas labajā vai kreisajā virzienā, ejot garām šai grupai no rindas uz rindu vai no kolonnas uz kolonnu. Kopumā tajā pašā laikā trīs skaitļu trīskāršu grupas griežas vienā virzienā. Vairāk sarežģīti gadījumi, trīs ekskluzīvu skaitļu pāri griežas vienā virzienā, bet trīskārši skaitļu griežas pretējā virzienā. Tātad, piemēram, ekskluzīvie cipari pirmajās trīs aplūkojamās problēmas rindās tiek pagriezti. Un, pats galvenais, šāda veida rotāciju var redzēt, ņemot vērā skaitļu atrašanās vietu apstrādātajā darblapā. Ar šo informāciju pagaidām pietiek, un citas rotācijas modeļa nianses sapratīsim problēmas risināšanas procesā.

Tātad pirmajās (augšējās) trīs rindās (1, 2 un 3) mēs varam pamanīt pāru (3+8) un (7+9), kā arī (2+x1) ar nezināmu x1 un singlu trīskāršs (x2+4+ 1) ar nezināmu x2. To darot, mēs varam secināt, ka katrs no x1 un x2 var būt vai nu 5, vai 6.

4., 5. un 6. rindā aplūkoti pāri (2+4) un (1+3). Jābūt arī trešajam nezināmajam pārim un singlu trīskāršam, no kuriem zināms tikai viens cipars 5.

Līdzīgi mēs aplūkojam 789. rindu, pēc tam kolonnu ABC, DEF un GHI trīskāršus. Apkopoto informāciju pierakstīsim simboliskā un, ceru, visai saprotamā formā:

Pagaidām šī informācija mums ir nepieciešama tikai, lai izprastu vispārējo situāciju. Rūpīgi pārdomājiet to, un tad mēs varam pāriet tālāk pie šādas īpaši šim nolūkam sagatavotas tabulas:

Alternatīvas izcēlu ar krāsām. Zils nozīmē "atļauts", bet dzeltens - "aizliegts". Ja, teiksim, atļauts A2=79 atļauts A2=7, tad C2=7 ir aizliegts. Vai arī otrādi – atļauts A2=9, aizliegts C2=9. Un tad atļaujas un aizliegumi tiek pārraidīti pa loģisku ķēdi. Šī krāsošana tiek veikta, lai būtu vieglāk aplūkot dažādas alternatīvas. Kopumā šī ir zināma līdzība ar "x-wing" un "swordfish" metodēm, kas minētas iepriekš, apstrādājot tabulas.

Apskatot opcijas B6=7 un attiecīgi B7=9, mēs uzreiz varam atrast divus punktus, kas nav savienojami ar šo opciju. Ja B7=9, tad rindās 789 rodas sinhroni rotējošs trīskāršs, kas nav pieļaujams, jo sinhroni (vienā virzienā) var griezties vai nu tikai trīs pāri (un tiem asinhroni trīs singli), vai trīs trīskārši (bez singliem). Turklāt, ja B7=9, tad pēc vairākām darblapas apstrādes soļiem 7. rindā konstatēsim nesaderību: B7=D7=9. Tāpēc mēs aizstājam vienīgo pieņemamo no abiem alternatīva B6=9, un tad problēma ir atrisināta vienkārši līdzekļi parasta apstrāde bez aklās uzskaites:

Tālāk man ir pabeigts piemērs izmantojot rotācijas modeli, lai atrisinātu problēmu no pasaules sudoku čempionāta, bet es izlaižu šo piemēru, lai pārāk neizstieptu šo rakstu. Turklāt, kā izrādījās, šai problēmai ir trīs risinājumi, kas ir slikti piemēroti sākotnējai ciparu rotācijas modeļa izstrādei. Es arī daudz pūžoju no interneta izvilkto Gerija Makgaira 17 taustiņu uzdevumu, lai atrisinātu viņa mīklu, līdz ar vēl lielāku īgnumu uzzināju, ka šai "mīklai" ir vairāk nekā 9 tūkstoši risinājumu.

Tā nu, gribot negribot, nākas pāriet pie Arto Inkala izstrādātās "visgrūtākās pasaulē" Sudoku problēmas, kurai, kā zināms, ir unikāls risinājums.

Pēc divu diezgan acīmredzamu ekskluzīvu skaitļu ievadīšanas un darblapas apstrādes uzdevums izskatās šādi:

Taustiņi iestatīti melnā krāsā un lielākā fontā ir sākotnējā problēma. Lai virzītos uz priekšu šīs problēmas risināšanā, mums atkal jāpaļaujas uz šim nolūkam piemērotu modeli. Šis modelis ir sava veida skaitļu rotācijas mehānisms. Par to jau ir runāts ne reizi vien šajā un iepriekšējos rakstos, taču, lai izprastu tālāko raksta materiālu, šis mehānisms būtu rūpīgi jāpārdomā un jāizstrādā. Apmēram tā, it kā ar šādu mehānismu būtu strādājis desmit gadus. Bet jūs tomēr varēsiet saprast šo materiālu, ja ne no pirmā lasījuma, tad no otrā vai trešā utt. Turklāt, ja jūs neatlaidīsieties, jūs nogādāsit šo "grūti saprotamo" materiālu tā ierastajā un vienkāršības stāvoklī. Šajā ziņā nav nekā jauna: tas, kas sākumā ir ļoti grūti, pamazām kļūst ne tik sarežģīts, un, turpinot nemitīgu pilnveidošanu, viss kļūst visredzamākais un neprasa prāta piepūli savā vietā, pēc kura jūs varat atbrīvot savu garīgo. turpmāka virzība uz risināmo problēmu vai citām problēmām.

Rūpīga Arto Inkala problēmas struktūras analīze parāda, ka visa problēma ir veidota uz trīs sinhroni rotējošu pāru un asinhroni rotējošu singlu pāru trīskārša principa: (x1+x2)+(x3+x4)+(x5+ x6)+(x7+x8+ x9). Rotācijas secība var būt, piemēram, šāda: pirmajās trīs rindās 123 pirmais pāris (x1+x2) iet no pirmā bloka pirmās rindas uz otrā bloka otro rindu, tad uz trešo. trešā bloka līnija. Otrais pāris lec no pirmā bloka otrās rindas uz otrā bloka trešo rindu, tad šajā rotācijā lec uz trešā bloka pirmo rindu. Trešais pāris no pirmā bloka trešās rindas pārlec uz otrā bloka pirmo rindu un pēc tam tajā pašā rotācijas virzienā pārlec uz trešā bloka otro rindu. Vienu trijotne pārvietojas līdzīgā rotācijas shēmā, bet pretējā virzienā nekā pāriem. Situācija ar kolonnām izskatās līdzīgi: ja tabulu garīgi (vai faktiski) pagriež par 90 grādiem, tad rindas kļūs par kolonnām ar tādu pašu singlu un pāru kustības raksturu kā iepriekš rindām.

Pārvēršot šīs rotācijas mūsu prātā saistībā ar Arto Incal problēmu, mēs pakāpeniski saprotam acīmredzamos ierobežojumus šīs rotācijas variantu izvēlei izvēlētajam rindu vai kolonnu trīskāršam:

Nevajadzētu būt sinhroni (vienā virzienā) rotējošiem trīnīšiem un pāriem - šādi trīnīši, atšķirībā no vientuļnieku tripleta, turpmāk tiks saukti par trīnīšiem;

Nedrīkst būt savstarpēji asinhroni pāri vai viens ar otru asinhroni singli;

Nedrīkst būt gan pāriem, gan vieniniekiem, kas rotē vienā (piemēram, pa labi) virzienā – tas ir iepriekšējo ierobežojumu atkārtojums, taču tas var šķist saprotamāk.

Turklāt ir arī citi ierobežojumi:

9 rindās nedrīkst būt neviens pāris, kas atbilst pārim nevienā no kolonnām, un tas pats attiecas uz kolonnām un rindām. Tam vajadzētu būt acīmredzamam: jo pats fakts, ka divi skaitļi atrodas vienā rindā, norāda, ka tie atrodas dažādās kolonnās.

Varat arī teikt, ka ļoti reti ir pāru sakritības dažādās rindu trīskāršās vai līdzīgas sakritības kolonnu trīskāršās, kā arī reti ir singlu trīskāršu atbilstības rindās un/vai kolonnās, bet tās ir, tā sakot. , varbūtības modeļi.

Pētījuma bloki 4,5,6.

4.-6.blokos ir iespējami pāri (3+7) un (3+9). Ja pieņemam (3+9), tad iegūstam nederīgu tripleta sinhrono rotāciju (3+7+9), tātad mums ir pāris (7+3). Pēc šī pāra aizstāšanas un turpmākās tabulas apstrādes ar parastajiem līdzekļiem mēs iegūstam:

Tajā pašā laikā mēs varam teikt, ka 5 B6=5 var būt tikai vientuļnieks, asinhrons (7+3), un 6 I5=6 ir paraģenerators, jo tas atrodas tajā pašā rindā H5=5 sestajā. bloks, un tāpēc tas nevar būt viens un var pārvietoties tikai sinhroni ar (7+3.

un sakārtoja vientuļu kandidātus pēc viņu parādīšanās šajā lomā šajā tabulā:

Ja pieņemam, ka visbiežāk sastopamie 2, 4 un 5 ir vieninieki, tad saskaņā ar rotācijas noteikumiem ar tiem var apvienot tikai pārus: (7 + 3), (9 + 6) un (1 + 8) - a pāris (1 + 9) ir atmests, jo tas noliedz pāri (9 + 6). Tālāk pēc šo pāru un vientuļu aizstāšanas un turpmāka apstrāde tabulas ar parastajām metodēm iegūstam:

Tāda nepaklausīga tabula izrādījās - to negribas apstrādāt līdz galam.

Jums būs smagi jāstrādā un jāpamana, ka kolonnās ABC ir pāris (7 + 4) un ka 6 šajās kolonnās pārvietojas sinhroni ar 7, tāpēc 6 ir pāra savienojums, tāpēc kolonnā ir iespējamas tikai kombinācijas (6 + 3). 4. bloka "C" +8 vai (6+8)+3. Pirmā no šīm kombinācijām nedarbojas, jo tad 7. blokā ailē "B" parādīsies nederīgs sinhronais trīskāršs - triplets (6 + 3 + 8). Nu, pēc opcijas (6 + 8) + 3 aizstāšanas un tabulas apstrādes parastajā veidā mēs nonākam pie veiksmīgas uzdevuma izpildes.

Otrais variants: atgriezīsimies pie tabulas, kas iegūta pēc kombinācijas (7 + 3) + 5 identificēšanas 456. rindā un pārejam pie kolonnu ABC izpētes.

Šeit mēs varam pamanīt, ka pāris (2+9) nevar notikt ABC. Citas kombinācijas (2+4), (2+7), (9+4) un (9+7) dod sinhronu trīskāršu - tripletu A4+A5+A6 un B1+B2+B3, kas ir nepieņemami. Paliek viens pieņemams pāris (7+4). Turklāt 6 un 5 sinhroni pārvietojas 7, kas nozīmē, ka tie ir tvaiku veidojoši, t.i. veido dažus pārus, bet ne 5 + 6.

Izveidosim iespējamo pāru sarakstu un to kombinācijas ar singliem:

Kombinācija (6+3)+8 neder, jo pretējā gadījumā vienā kolonnā (6 + 3 + 8) tiek izveidots nederīgs triple-triplets, kas jau ir apspriests un ko mēs varam vēlreiz pārbaudīt, pārbaudot visas opcijas. No vieninieku kandidātiem visvairāk punktu iegūst 3. numurs, un visticamāk no visām iepriekš minētajām kombinācijām: (6 + 8) + 3, t.i. (C4=6 + C5=8) + C6=3, kas dod:

Turklāt visticamākais kandidāts vieniniekiem ir 2 vai 9 (katrs 6 punkti), bet jebkurā no šiem gadījumiem 1. kandidāts (4 punkti) paliek spēkā. Sāksim ar (5+29)+1, kur 1 ir asinhroni ar 5, t.i. ievietojiet 1 no B5=1 kā asinhronu singlu visās ABC kolonnās:

7. blokā A ailē ir iespējamas tikai opcijas (5+9)+3 un (5+2)+3. Bet labāk pievērsiet uzmanību tam, ka 1.-3. rindā tagad ir parādījušies pāri (4 + 5) un (8 + 9). To aizstāšana noved pie ātra rezultāta, t.i. līdz uzdevuma pabeigšanai pēc tam, kad tabula ir apstrādāta ar parastajiem līdzekļiem.

Nu, tagad, praktizējot iepriekšējās iespējas, mēs varam mēģināt atrisināt Arto Incal problēmu, neiesaistot statistiskās aplēses.

Mēs atkal atgriežamies sākuma pozīcijā:

4.-6.blokos ir iespējami pāri (3+7) un (3+9). Ja mēs pieņemam (3 + 9), mēs iegūstam nederīgu tripleta sinhrono rotāciju (3 + 7 + 9), tāpēc aizvietošanai tabulā mums ir tikai iespēja (7 + 3):

5 šeit, kā redzam, ir vientuļnieks, 6 ir paraformētājs. Derīgās opcijas ABC5: (2+1)+8, (2+1)+9, (8+1)+9, (8+1)+2, (9+1)+8, (9+1) +2. Bet (2+1) ir asinhrons ar (7+3), tāpēc ir (8+1)+9, (8+1)+2, (9+1)+8, (9+1)+2. Jebkurā gadījumā 1 ir sinhrons (7 + 3) un tādējādi paraģenerējošs. Aizstāsim tabulā 1 šajā statusā:

Skaitlis 6 šeit ir paraģenerators bl. 4-6, bet uzkrītošā pāris (6+4) nav derīgo pāru sarakstā. Tādējādi četrstūris A4=4 ir asinhrons 6:

Tā kā D4+E4=(8+1) un saskaņā ar rotācijas analīzi veido šo pāri, mēs iegūstam:

Ja šūnas C456=(6+3)+8, tad B789=683, t.i. iegūstam sinhronu trīskāršu-tripletu, tāpēc mums paliek iespēja (6+8)+3 un tās aizstāšanas rezultāts:

B2=3 šeit ir viens, C1=5 (asinhronais 3) ir savienošana pārī, A2=8 ir arī savienošana pārī. B3=7 var būt gan sinhrons, gan asinhrons. Tagad varam sevi pierādīt sarežģītākos trikos. Ar trenētu aci (vai vismaz pārbaudot datorā) redzam, ka jebkuram statusam B3=7 - sinhrons vai asinhrons - iegūstam tādu pašu rezultātu A1=1. Tāpēc mēs varam aizstāt šo vērtību ar A1 un pēc tam izpildīt mūsu vai drīzāk Arto Incala uzdevumu ar ierastākiem vienkāršiem līdzekļiem:

Tā vai citādi, mēs varējām apsvērt un pat ilustrēt trīs vispārīgas pieejas problēmu risināšanai: noteikt problēmas izpratnes punktu (nevis hipotētisku vai akli deklarētu, bet reālu brīdi, no kura var runāt par problēmas izpratni ), izvēlieties modeli, kas ļauj mums realizēt izpratni, izmantojot dabisku vai mentālu eksperimentu, un, treškārt, šajā gadījumā sasniegto rezultātu izpratnes un uztveres pakāpi novest līdz pašsaprotamības un vienkāršības stāvoklim. Ir arī ceturtā pieeja, ko es personīgi izmantoju.

Katram cilvēkam ir stāvokļi, kad intelektuālie uzdevumi un problēmas, ar kurām viņš saskaras, tiek atrisinātas vieglāk nekā parasti. Šie stāvokļi ir diezgan atkārtojami. Lai to izdarītu, jums jāapgūst domu izslēgšanas tehnika. Sākumā vismaz uz sekundes daļu, pēc tam arvien vairāk stiepjot šo atvienošanas brīdi. Es nevaru pateikt, vai drīzāk ieteikt kaut ko šajā sakarā, jo šīs metodes piemērošanas ilgums ir tīri personisks jautājums. Bet es ķeros pie šīs metodes dažreiz ilgu laiku, kad manā priekšā rodas problēma, kurai es neredzu variantus, kā tai pieiet un atrisināt. Rezultātā agri vai vēlu no atmiņu krātuvēm iznirst piemērots modeļa prototips, kas noskaidro risināmā būtību.

Es atrisināju Inkalas problēmu vairākos veidos, ieskaitot iepriekšējos rakstos aprakstītos. Un vienmēr tā vai citādi es izmantoju šo ceturto pieeju ar izslēgšanos un sekojošu garīgo spēku koncentrēšanu. Es ieguvu ātrāko problēmas risinājumu, izmantojot vienkāršu uzskaitījumu - to, ko sauc par "poke metodi", taču, izmantojot tikai "garās" iespējas: tās, kas ātri varētu novest pie pozitīva vai negatīva rezultāta. Citas iespējas no manis prasīja vairāk laika, jo lielākā daļa laika tika veltīta vismaz aptuvenai šo iespēju izmantošanas tehnoloģijas izstrādei.

Labs risinājums ir arī ceturtās pieejas garā: noskaņojieties Sudoku problēmu risināšanai, problēmas risināšanas procesā aizvietojot tikai vienu ciparu katrā šūnā. Tas ir, lielākā daļa uzdevuma un tā datu tiek "ritināti" prātā. Šī ir galvenā intelektuālo problēmu risināšanas procesa daļa, un šī prasme ir jāapmāca, lai palielinātu spēju risināt problēmas. Piemēram, es neesmu profesionāls Sudoku risinātājs. Man ir citi uzdevumi. Bet tomēr es vēlos izvirzīt sev šādu mērķi: apgūt spēju risināt paaugstinātas sarežģītības Sudoku problēmas bez darblapas un neaizstājot vairāk nekā vienu ciparu vienā tukšā šūnā. Šajā gadījumā ir atļauts jebkurš Sudoku risināšanas veids, ieskaitot vienkāršu opciju uzskaitījumu.

Tā nav nejaušība, ka es šeit atceros iespēju uzskaitījumu. Jebkura pieeja Sudoku problēmu risināšanai ietver noteiktu metožu kopumu savā arsenālā, tostarp viena vai cita veida uzskaitīšanu. Tajā pašā laikā jebkurai no metodēm, kas tiek izmantotas īpaši Sudoku vai citu problēmu risināšanā, ir sava joma. efektīva pielietošana. Tātad, pieņemot lēmumu par vienkāršus uzdevumus Sudoku vienkāršās "pamata" metodes ir visefektīvākās, kas aprakstītas daudzos rakstos par šo tēmu internetā, un sarežģītākā "rotācijas metode" šeit bieži vien ir bezjēdzīga, jo tas tikai sarežģī kursu vienkāršs risinājums un tajā pašā laikā tas nesniedz nekādu jaunu informāciju, kas parādās problēmas risināšanas gaitā. Bet vissarežģītākajos gadījumos, piemēram, Arto Inkala problēmai, "rotācijas metodei" var būt galvenā loma.

Manos rakstos Sudoku ir tikai ilustratīvs piemērs problēmu risināšanas pieejām. Starp manis atrisinātajām problēmām ir arī daudz grūtākas problēmas nekā Sudoku. Piemēram, kas atrodas mūsu vietnē datoru modeļi katlu un turbīnu darbība. Es arī neiebilstu par viņiem runāt. Bet pagaidām es izvēlējos Sudoku, tāpēc pietiek vizuāli parādiet saviem jaunajiem līdzpilsoņiem iespējamie veidi un progresa posmi ceļā uz risināmo problēmu galīgo mērķi.

Tas šodienai viss.

Sveiki! Šajā rakstā mēs detalizēti analizēsim sarežģītā Sudoku risinājumu, izmantojot konkrētu piemēru. Pirms analīzes sākšanas mēs vienojamies nosaukt mazos kvadrātus ar skaitļiem, numurējot tos no kreisās puses uz labo un no augšas uz leju. Visi Sudoku risināšanas pamatprincipi ir aprakstīti šajā rakstā.

Kā parasti, vispirms apskatīsim atklātos singlus. Un tādi b5-5, e6-3 bija tikai divi. Tālāk mēs ievietojam iespējamos kandidātus visos tukšajos laukos.

Kandidāti tiks ievietoti mazā drukā Zaļā krāsa lai atšķirtu no jau stāvošiem cipariem. Mēs to darām mehāniski, vienkārši šķirojot visas tukšās šūnas un ievadot tajās skaitļus, kas tajās var būt.

Mūsu darba augļus var redzēt 2. attēlā. Pievērsīsim uzmanību šūnai f2. Viņai ir divi kandidāti 5 un 9. Mums būs jāizmanto minēšanas metode, un kļūdas gadījumā jāatgriežas pie šīs izvēles. Ieliksim piekto numuru. Noņemsim pieci no f rindas, 2. kolonnas un ceturtā kvadrāta kandidātiem.

Mēs pastāvīgi noņemsim iespējamos kandidātus pēc numura iestatīšanas, un šajā rakstā mēs vairs nekoncentrēsimies uz to!

Mēs skatāmies tālāk uz ceturto kvadrātu, mums ir tee - tās ir šūnas e1, d2, e3, kurās ir kandidāti 2, 8 un 9. Noņemsim tos no pārējām ceturtā kvadrāta neaizpildītajām šūnām. Dodieties tālāk. Sestajā laukumā skaitlis pieci var būt tikai uz e8.

Vairāk par Šis brīdis nav ne pāru, ne teeju, nemaz nerunājot par četriniekiem. Tāpēc iesim citu ceļu. Iziesim cauri visām vertikālēm un horizontālēm, lai noņemtu nevajadzīgos kandidātus.

Un tā otrajā vertikālē skaitlis 8 var būt tikai šūnās -h2 un i2, noņemsim skaitli astoņi no pārējām neaizpildītām septītā kvadrāta šūnām. Trešajā failā skaitlis astoņi var būt tikai e3. Tas, ko mēs ieguvām, ir parādīts 3. attēlā.

Nav vairs pie kā ķerties. Mums ir diezgan ciets rieksts, bet mēs to tik un tā pārplēsim! Un tā, vēlreiz apsveriet mūsu pāri e1 un d2, sakārtojiet to šādā veidā d2-9, e1 -2. Un mūsu kļūdas gadījumā mēs atkal atgriezīsimies pie šī pāra.

Tagad mēs varam droši ierakstīt deuce šūnā d9! Un laukumā ir septiņi, deviņi var būt tikai uz h1. Pēc tam uz vertikāles 1 piecinieks var būt tikai uz i1, kas savukārt dod tiesības ievietot piecinieku uz h9 šūnas.

4. attēlā parādīts mūsu paveiktais. Tagad apsveriet nākamo pāri, tie ir d3 un f1. Viņiem ir kandidāti 7 un 6. Skatoties uz priekšu, teikšu, ka izkārtojuma variants d3-7, f1-6 ir kļūdains un rakstā to neapskatīsim, lai netērētu laiku.

5. attēls ilustrē mūsu darbu. Kas mums atliek darīt tālāk? Protams, vēlreiz izejiet cauri skaitļu iestatīšanas iespējām! Šūnā g1 ievietojam trīskāršu. Saglabājiet kā vienmēr, lai varētu atgriezties. Viens ir iestatīts uz i3. tagad septītajā kvadrātā iegūstam pāri h2 un i2, ar skaitļiem 2 un 8. Tas dod mums tiesības izslēgt šos skaitļus no kandidātiem visai neaizpildītai vertikālei.

Pamatojoties uz pēdējo tēzi, mēs sakārtojam. a2 ir četrinieks, b2 ir trīs. Un pēc tam varam nolikt visu pirmo laukumu. c1 - seši, a1 - viens, b3 - deviņi, c3 - divi.

6. attēlā parādīts, kas notika. Uz i5 mums ir paslēpts vientuļnieks - numurs trīs! Un i2 var būt tikai numurs 2! Attiecīgi h2 - 8.

Tagad pievērsīsimies šūnām e4 un e7, šis ir pāris ar kandidātiem 4 un 9. Sakārtosim tos šādi: e4 četri, e7 deviņi. Tagad sešinieks ir novietots uz f6, un deviņi ir novietoti uz f5! Tālāk uz c4 mēs iegūstam slēpto vientuļnieku - numuru deviņi! Un mēs varam uzreiz likt četrus no 8 un pēc tam aizvērt horizontāli ar: c6 astoņi.

SUDOKU ir populāra atjautības spēle, kas ir skaitļu mīkla, kuru var pārvarēt, tikai veidojot loģiskus secinājumus. Nosaukumā Sudoku, kas tulkots no japāņu valodas, “su” nozīmē “skaitlis”, bet doku “doku” nozīmē “stāvēt atsevišķi”. Tāpēc "SUDOKU" aptuveni nozīmē "viencipara".

Nosaukumu "Sudoku" šai mīklai piešķīra japāņu izdevējs Nicoli 1984. gadā. Sudoku ir saīsinājums vārdam "Suuji wa dokushin ni kagiru", kas japāņu valodā nozīmē "jābūt tikai vienam skaitlim". Izdevējs Nikoli ne tikai nāca klajā ar skanīgu nosaukumu, bet arī pirmo reizi ieviesa simetriju savu mīklu uzdevumos. Puzles nosaukumu deva Nikoli līderis - Kaji Maki. Visa pasaule pieņēma šo jauno japāņu nosaukumu, bet pašā Japānā mīklu sauc par "Nanpure". Nicoli savā valstī ir reģistrējis vārdu "Sudoku" kā preču zīmi.

SUDOKU izcelsme

Indija tiek uzskatīta par šaha dzimteni, Anglija tiek uzskatīta par futbola dzimteni. Sudoku spēlei (sudoku), kas ātri izplatījās visā pasaulē, nav dzimtenes kā tādas. Par Sudoku prototipu var uzskatīt mīklu Magic Square, kas parādījās Ķīnā pirms 2000 gadiem.

Sudoku kā spēles vēsture aizsākās līdz slavenajam Šveices matemātiķim, mehāniķim un fiziķim Leonhardam Eileram (1707–1783).

Viņa arhīva dokumentos, kas datēti ar 1776. gada 17. oktobri, ir piezīmes par to, kā izveidot burvju kvadrātu ar noteiktu skaitušūnas, īpaši 9., 16., 25. un 36. Citā dokumentā ar nosaukumu " Zinātniskie pētījumi jaunas maģiskā kvadrāta šķirnes " Eilers ievietots šūnās vēstules(Latīņu kvadrāts), vēlāk viņš aizpildīja kameras grieķu burti un sauca kvadrātu grieķu-latīņu valodā. Izpēte dažādas iespējas burvju kvadrāts, Eilers vērsa uzmanību uz problēmu, kas saistīta ar simbolu apvienošanu tā, lai neviens no tiem neatkārtotos nevienā rindā un nevienā kolonnā.

AT moderna forma Sudoku mīklas pirmo reizi tika publicētas 1979. gadā žurnālā Word Games. Puzles autors bija Hārvards Gariss no Indiānas. Puzle "Numura vieta" (tulkojumā krievu valodā - "skaitļa vieta") - to var uzskatīt par vienu no pirmajiem mūsdienu Sudoku izlaidumiem. Tas pievienoja 3x3 šūnu blokus, kas bija svarīgs uzlabojums, jo tas ļāva padarīt mīklu interesantāku. Viņš izmantoja Eilera latīņu kvadrāta principu, piemēroja to 9x9 matricā un pievienoja papildu ierobežojumus, skaitļus nevajadzētu atkārtot iekšējos 3x3 kvadrātos.

Tādējādi Sudoku ideja nenāca no Japānas, kā daudzi domā, bet spēles nosaukums patiešām ir japāņu valodā.

Japānā šo mīklu publicēja Nicoly Inc., lielākais dažādu mīklu kolekciju izdevējs, laikrakstā Monthly Nicolist 1984. gada aprīlī ar nosaukumu "Numuru var izmantot tikai vienu reizi". 2004. gada 12. novembrī The Times savās lapās publicēja pirmo Sudoku mīklu. Šī publikācija kļuva par sensāciju, mīkla ātri izplatījās visā Lielbritānijā, Austrālijā, Jaunzēlandē; ieguva popularitāti ASV.

Sudoku varianti

Tātad, kas ir Sudoku? Pašlaik šim populārajam mīklu veidam ir daudz jauninājumu, taču klasiskais Sudoku ir 9 x 9 kvadrāts, kas sadalīts apakšlaukumos ar 3 šūnām katrā. Tādējādi kopējais spēles laukums ir 81 šūna. Pielikumā savam darbam ielikšu dažādi veidi Sudoku un iespējamie risinājumi (man vecāki palīdzēja tos atrisināt).

Sudoku grūtības pakāpes atšķiras atkarībā no laukuma lieluma:

• 1. Mazajiem mīklu cienītājiem Sudoku ir izveidots ar 2x2, 6x6 šūnu laukiem.
• 2. Profesionāļiem ir Sudoku 15x15 un 16x16 šūnas

Ir Sudoku dažādi līmeņi:

• viegli
• vidēji
• sarežģīti
• ļoti sarežģīti
• super komplekss

Lēmuma noteikumi

Sudoku mīklām ir tikai viens noteikums. Brīvās šūnas jāaizpilda tā, lai katrā rindā, katrā kolonnā un katrā mazajā 3X3 kvadrātā katrs skaitlis no 1 līdz 9 parādītos tikai 1 reizi. Dažas Sudoku šūnas jau ir aizpildītas ar cipariem, un pārējās ir jāaizpilda jums. Jo vairāk skaitļu sākotnēji, jo vieglāk ir atrisināt mīklu. Starp citu, pareizi sastādītam Sudoku ir tikai viens risinājums.

Sudoku risinājums

Sudoku risināšanas stratēģija ietver trīs soļus:

• apgūstot skaitļu atrašanās vietu mīklā
• iepriekšēja skaitļu sakārtošana
• analīze

Labākais veids risinājumi - ierakstiet kandidātu numurus šūnas kreisā stūra augšdaļā. Pēc tam jūs varat redzēt tieši tos skaitļus, kuriem vajadzētu aizņemt šo šūnu. Sudoku jāspēlē lēni, jo tā ir relaksējoša spēle. Dažas mīklas var atrisināt dažu minūšu laikā, bet citas var aizņemt stundas vai dažos gadījumos pat dienas.

Matemātiskā bāze. Iespējamo kombināciju skaits 9x9 Sudoku ir 6 670 903 752 021 072 936 960 pēc Bertama Felgenhauera aprēķiniem.

Kas jums palīdzēs viena no svarīgākajiem orgāniem - smadzeņu attīstībā. Protams, viena no tām ir labi zināmās japāņu sudoku mīklas. Ar viņu palīdzību jūs varat diezgan “uzpumpēt smadzenes”, jo papildus tam, ka ir jāaprēķina milzīgs skaits skaitļu izkārtojuma iespēju, jums tas arī jāspēj izdarīt pāris desmitus kustību uz priekšu. Vārdu sakot, šī ir īsta paradīze, ja vēlaties, lai jūsu neironi neizžūtu. Un šodien mēs apskatīsim galvenos trikus, ko izmanto Sudoku eksperti. Noderēs gan iesācējiem, gan jau seniem šo mīklu cienītājiem. Galu galā kādam ir jāsper pirmie soļi Sudoku mākslā, un kādam ir jāuzlabo savu lēmumu efektivitāte!

noteikumiem

Ja jūs vēl neesat iepazinies ar noteikumiem, vispirms jums vajadzētu iepazīties ar noteikumiem. Ticiet man, tie ir ļoti vienkārši.

Spēles laukums ir kvadrāts, kura izmēri ir 9 × 9. Tajā pašā laikā tas ir sadalīts mazākos kvadrātos ar izmēriem 3 × 3. Tas ir, viss lauks sastāv no 81 šūnas.

Problēmas nosacījums ir skaitļi, kas jau ir ievietoti šajās šūnās.

Bloks (šūnu bloks) - mazs kvadrāts, līnija vai līnija.

Kas jums jādara: sakārtojiet visus pārējos numurus, ievērojot dažus noteikumus. Pirmkārt, katrā mazajā kvadrātā nevajadzētu būt atkārtojumiem. Otrkārt, visās kolonnās un rindās nedrīkst būt arī atkārtojumu. Tas nozīmē, ka katram skaitlim katrā no šiem blokiem ir jāatrodas tikai vienu reizi. Lai viss būtu vēl skaidrāks, pievērsiet uzmanību atrisinātajam Sudoku:

Pamata risinājums

Parasti, ja jūs atrisinat vienkāršu Sudoku, tad viss, kas jums jādara, ir jāpieraksta visas iespējamās iespējas katrai no 81 šūnām un pakāpeniski jāizsvītro nepiemērotās iespējas. Tas ir ļoti vienkārši.

Bet, ja paceļaties par līmeni uz sarežģītāku Sudoku, lietas kļūst interesantākas. Bieži gadās, ka nav iespējas ievietot jaunus skaitļus, un jums būs jāiziet cauri pieņēmumiem: “Lai ir tāds skaitlis”, pēc kura jums būs jāapsver šī hipotēze un vai nu jārod risinājums. problēma vai jūsu pieņēmuma pretruna.

Taču, protams, ir īpaši triki, kas palīdzēs to visu paveikt efektīvāk.

triki

1. Kailie pāri/trīs/četrinieki

Ja vienā blokā (kvadrāts, rinda vai kolonna) ir divas šūnas, kurās var ievietot tikai 2 skaitļus, tad ir acīmredzams, ka šo skaitļu var izņemt no iespējamām opcijām citām šī bloka šūnām.

Turklāt šo triku var viegli izdarīt gan ar trīskāršiem, gan četriem:

2. Slēptie pāri

Ļoti noderīgs paņēmiens, savā ziņā pretējs kailajiem pāriem. Ja kādās divās viena kvadrāta šūnās iespējas” jums ir skaitļi, kas nekur citur neatkārtojas (šajā kvadrātā), tad visus pārējos skaitļus no šīm divām šūnām var noņemt.

Lai padarītu to vēl skaidrāku, pievērsiet uzmanību piemēriem (viens vienkāršs un sarežģītāks):

Par laimi, tas darbojas gan trīskāršiem, gan četriem, taču ir vērts pieminēt ļoti svarīgu un ļoti foršu funkciju. Nav nepieciešams, lai trīs/četrās šūnās būtu vienādi 3 formas (a;b;c) (a;b;c) (a;b;c) cipari. Jums pietiks ar šo opciju: (a;b) (b;c) (a;c).

3. Bezvārda likums

Ja jums vienā kolonnā/rindā ir pāris vai trīskārši, kas atrodas tajā pašā kvadrātā, varat droši noņemt šos skaitļus no citām šī kvadrāta šūnām.

4. Rādītāju pāri

Ja vienā rindā/kolonnā “opcijās” ir divas opcijas vienādi cipari, tad šādus skaitļus var izņemt no atbilstošās kolonnas/rindas.

Reizēm tas var būt ļoti noderīgi, īpaši, ja atrodat vairākus no šiem pāriem:

Protams, šajā gadījumā šiem skaitļiem nevajadzētu būt citās kvadrāta šūnās, taču saskaņā ar nenosaukto noteikumu tas nav nepieciešams.

Vai jums patīk Sudoku un citas mīklas, spēles, mīklas un testi, kuru mērķis ir attīstīt dažādus domāšanas aspektus? Piekļūstiet visiem vietnes interaktīvajiem materiāliem, lai tos efektīvāk izstrādātu.

Secinājums

Mēs esam pārskatījuši pamata metodes, kas tiek izmantotas Sudoku risināšanā. Es atzīmēju, ka tas ir tikai sākums, un nākamajos rakstos mēs apsvērsim sarežģītākas un interesantākas mikroshēmas, pateicoties kurām šādu problēmu risināšana kļūs vēl interesantāka un vienkāršāka.

Kā apmācību 4brain izdevums aicina jūs iepazīties ar failu, kurā ir sudoku dažādi līmeņi grūtības. Veltiet laiku praksei, jo, ja veltīsiet šai nodarbībai pietiekami daudz laika, tad šī rakstu kursa beigās, ticiet man, jūs kļūsiet par īstu dūzi japāņu mīklu risināšanā.

Ja jums ir kādi jautājumi par šīm metodēm vai Sudoku, ko pievienojam rakstam, droši uzdodiet tos komentāros!