REĀLIE SKAITĻI II

§ 44 Reālu skaitļu ģeometriskais attēlojums

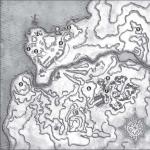
Ģeometriski reāli skaitļi, tāpat kā racionālie skaitļi, tiek attēloti ar punktiem uz taisnas līnijas.

Ļaujiet l - patvaļīga taisne, un O - daži tās punkti (58. att.). Katrs pozitīvs reālais skaitlis α ievietojiet atbilstības punktu A, kas atrodas pa labi no O attālumā no α garuma vienības.

Ja, piemēram, α = 2,1356..., tad

2 < α < 3
2,1 < α < 2,2
2,13 < α < 2,14

utt. Ir skaidrs, ka punktam A šajā gadījumā ir jāatrodas uz taisnes l pa labi no punktiem, kas atbilst skaitļiem

2; 2,1; 2,13; ... ,

bet pa kreisi no skaitļiem atbilstošajiem punktiem

3; 2,2; 2,14; ... .

Var parādīt, ka šie nosacījumi ir definēti uz līnijas l vienīgais punkts A, kuru mēs uzskatām par reāla skaitļa ģeometrisko attēlu α = 2,1356... .

Tāpat katrs negatīvs reālais skaitlis β savietojiet punktu B, kas atrodas pa kreisi no O attālumā | β | garuma vienības. Visbeidzot, mēs piešķiram punktu O skaitlim "nulle".

Tātad skaitlis 1 tiks parādīts taisnā līnijā l punkts A, kas atrodas pa labi no O vienas garuma vienības attālumā (59. att.), skaitlis - √2 - punkts B, kas atrodas pa kreisi no O √2 garuma vienību attālumā utt.

Parādīsim, kā uz taisnas līnijas l izmantojot kompasu un lineālu, jūs varat atrast punktus, kas atbilst reālajiem skaitļiem √2, √3, √4, √5 utt. Lai to izdarītu, vispirms parādīsim, kā izveidot segmentus, kuru garumus izsaka ar šie skaitļi. Lai AB ir segments, kas ņemts par garuma vienību (60. att.).

Punktā A mēs atjaunojam perpendikulu šim segmentam un uz tā novietojam segmentu AC, kas vienāds ar segmentu AB. Tad, pielietojot Pitagora teorēmu taisnleņķa trijstūrim ABC, iegūstam; BC \u003d √AB 2 + AC 2 \u003d √1 + 1 \u003d √2

Tāpēc segmenta BC garums ir √2. Tagad atjaunosim nogriežņa BC perpendikulu punktā C un izvēlēsimies tajā punktu D, lai segments CD būtu vienāds ar vienu AB garums. Tad no taisnleņķa trīsstūris BCD atradums:

ВD \u003d √BC 2 + CD 2 \u003d √2 + 1 \u003d √3

Tāpēc segmenta BD garums ir √3. Turpinot aprakstīto procesu tālāk, varētu iegūt segmentus BE, BF, ..., kuru garumus izsaka ar skaitļiem √4, √5 utt.

Tagad uz līnijas l ir viegli atrast tos punktus, kas kalpo kā skaitļu √2, √3, √4, √5 utt. ģeometrisks attēlojums.

Noliekot, piemēram, pa labi no punkta O nogriezni BC (61. att.), iegūstam punktu C, kas kalpo kā skaitļa √2 ģeometrisks attēlojums. Tādā pašā veidā, atliekot nogriezni BD pa labi no punkta O, iegūstam punktu D", kas ir skaitļa √3 ģeometriskais attēls utt.

Tomēr nevajadzētu domāt, ka ar kompasa un lineāla palīdzību uz skaitļu līnijas l var atrast punktu, kas atbilst jebkuram reālam skaitlim. Piemēram, ir pierādīts, ka, ja jūsu rīcībā ir tikai kompass un lineāls, nav iespējams izveidot segmentu, kura garums ir izteikts ar skaitli π = 3,14 ... . Tātad uz skaitļu līnijas l Izmantojot šādas konstrukcijas, nav iespējams norādīt šim skaitlim atbilstošu punktu, tomēr šāds punkts pastāv.

Tātad katram reālajam skaitlim α ir iespējams saistīt kādu precīzi definētu līnijas punktu l . Šis punkts tiks atdalīts no sākuma punkta O attālumā | α | garuma vienībām un jābūt pa labi no O, ja α > 0 un pa kreisi no O, ja α < 0. Очевидно, что при этом двум неравным действительным числам будут соответствовать две dažādi punkti taisni l . Patiešām, ļaujiet skaitlim α atbilst punktam A un skaitlim β - punkts B. Tad, ja α > β , tad A būs pa labi no B (62. att., a); ja α < β , tad A atradīsies pa kreisi no B (62. att., b).

Runājot 37. § par racionālu skaitļu ģeometrisko attēlojumu, mēs uzdevām jautājumu: vai jebkuru taisnes punktu var uzskatīt par ģeometrisku attēlu racionāls skaitļi? Toreiz mēs nevarējām sniegt atbildi uz šo jautājumu; tagad mēs uz to varam atbildēt pavisam noteikti. Uz taisnas līnijas ir punkti, kas kalpo kā ģeometrisks attēls iracionāli skaitļi(piemēram, √2). Tāpēc ne katrs taisnes punkts ir racionāls skaitlis. Bet šajā gadījumā rodas cits jautājums: vai jebkuru reālās līnijas punktu var uzskatīt par dažu ģeometrisku attēlu derīgs skaitļi? Šis jautājums jau ir pozitīvi atrisināts.

Patiešām, lai A ir patvaļīgs punkts uz taisnes l , kas atrodas pa labi no O (63. att.).

Segmenta OA garumu izsaka ar kādu pozitīvu reālo skaitli α (sk. 41. §). Tāpēc punkts A ir skaitļa ģeometriskais attēls α . Tāpat tiek konstatēts, ka katru punktu B, kas atrodas pa kreisi no O, var uzskatīt par negatīva reālā skaitļa ģeometrisku attēlu - β , kur β - segmenta VO garums. Visbeidzot, punkts O kalpo kā skaitļa nulles ģeometrisks attēlojums. Ir skaidrs, ka divi atšķirīgi līnijas punkti l nevar būt tā paša reālā skaitļa ģeometriskais attēls.

Iepriekš minēto iemeslu dēļ tiek saukta taisne, uz kuras kāds punkts O ir norādīts kā "sākotnējais" punkts (noteiktai garuma vienībai). skaitļa līnija.

Secinājums. Visu reālo skaitļu kopa un visu reālās līnijas punktu kopa atrodas viens pret vienu.

Tas nozīmē, ka katrs reālais skaitlis atbilst vienam, precīzi definētam skaitļu līnijas punktam, un, otrādi, katram skaitļu līnijas punktam ar šādu atbilstību atbilst viens, precīzi definēts reālais skaitlis.

Vingrinājumi

320. Noskaidro, kurš no diviem punktiem atrodas uz skaitļu līnijas pa kreisi un kurš pa labi, ja šie punkti atbilst skaitļiem:

a) 1,454545... un 1,455454...; c) 0 un - 1,56673...;

b) - 12,0003... un - 12,0002...; d) 13.24... un 13.00....

321. Noskaidro, kurš no diviem punktiem atrodas tālāk no skaitļu līnijas sākuma punkta O, ja šie punkti atbilst skaitļiem:

a) 5,2397... un 4,4996...; .. c) -0,3567... un 0,3557... .

d) - 15,0001 un - 15,1000...;

322. Šajā sadaļā tika parādīts, ka konstruēt segmentu ar garumu √ n izmantojot kompasu un taisngriezi, varat rīkoties šādi: vispirms izveidojiet segmentu ar garumu √2, pēc tam segmentu ar garumu √3 utt., līdz mēs sasniedzam segmentu ar garumu √ n . Bet par katru fiksēto P > 3 šo procesu var paātrināt. Kā jūs, piemēram, sāktu veidot segmentu, kura garums ir √10?

323*. Kā izmantot kompasu un lineālu, lai atrastu punktu uz skaitļa līnijas, kas atbilst skaitlim 1 / α , ja skaitlim atbilstošā punkta pozīcija α , zināms?

Skaitļa līnija, skaitļa ass, ir līnija, uz kuras ir attēloti reāli skaitļi. Uz taisnes tiek izvēlēta sākumpunkts - punkts O (punkts O apzīmē 0) un punkts L, kas attēlo vienību. Punkts L parasti atrodas pa labi no punkta O. Nogriezni OL sauc par vienības segmentu.

Punkti pa labi no punkta O apzīmē pozitīvus skaitļus. Punkti pa kreisi no punkta. Ak, attēlojiet negatīvus skaitļus. Ja punkts X apzīmē pozitīvu skaitli x, tad attālums OX = x. Ja punkts X apzīmē negatīvu skaitli x, tad attālums OX = - x.

Skaitli, kas parāda punkta pozīciju uz taisnes, sauc par šī punkta koordinātu.

Attēlā redzamā punkta V koordinātas ir 2, bet punkta H koordinātas ir -2,6.

Reālā skaitļa modulis ir attālums no sākuma līdz punktam, kas atbilst šim skaitlim. Norādiet skaitļa x moduli, tātad: | x |. Acīmredzot, | 0 | = 0.

Ja skaitlis x ir lielāks par 0, tad | x | = x, un, ja x ir mazāks par 0, tad | x | = - x. Uz šīm moduļa īpašībām balstās daudzu vienādojumu un nevienādību risinājums ar moduli.

Piemērs: Atrisiniet vienādojumu | x - 3 | = 1.

Risinājums: Apsveriet divus gadījumus - pirmo gadījumu, kad x -3 > 0, un otro gadījumu, kad x - 3 0.

1. x - 3 > 0, x > 3.

Šajā gadījumā | x - 3 | = x - 3.

Vienādojums ir šādā formā: x - 3 \u003d 1, x \u003d 4. 4\u003e 3 - atbilst pirmajam nosacījumam.

2. x -3 0, x 3.

Šajā gadījumā | x - 3 | = - x + 3

Vienādojums ir x + 3 \u003d 1, x \u003d - 2. -2 3 - atbilst otrajam nosacījumam.

Atbilde: x = 4, x = -2.

Skaitliskās izteiksmes.

Skaitliskā izteiksme ir viena vai vairāku skaitļu un funkciju kopums, kas savienoti ar aritmētiskajiem operatoriem un iekavām.
Skaitlisko izteiksmju piemēri:

Skaitliskās izteiksmes vērtība ir skaitlis.
Darbības skaitliskā izteiksmē tiek veiktas šādā secībā:

1. Darbības iekavās.

2. Funkciju aprēķins.

3. Paaugstināšana

4. Reizināšana un dalīšana.

5. Saskaitīšana un atņemšana.

6. Viena veida darbības tiek veiktas no kreisās puses uz labo.

Tātad pirmās izteiksmes vērtība būs pats skaitlis 12.3
Lai aprēķinātu otrās izteiksmes vērtību, mēs veiksim darbības šādā secībā:

1. Iekavās norādītās darbības veiciet šādā secībā — vispirms paaugstinām 2 līdz trešajai pakāpei, pēc tam no iegūtā skaitļa atņemam 11:

3 4 + (23 - 11) = 3 4 + (8 - 11) = 3 4 + (-3)

2. Reiziniet 3 ar 4:

3 4 + (-3) = 12 + (-3)

3. Veiciet darbības secīgi no kreisās puses uz labo:

12 + (-3) = 9.
Izteiksme ar mainīgajiem ir viena vai vairāku skaitļu, mainīgo un funkciju kopums, kas savienots ar aritmētiskajiem operatoriem un iekavām. Izteiksmju vērtības ar mainīgajiem ir atkarīgas no tajā iekļauto mainīgo vērtībām. Darbību secība šeit ir tāda pati kā skaitliskām izteiksmēm. Dažkārt lietderīgi ir vienkāršot izteiksmes ar mainīgajiem, veicot dažādas darbības - iekavas, iekavas paplašināšanu, grupēšanu, daļskaitļu samazināšanu, līdzīgu samazināšanu utt. Tāpat izteiksmju vienkāršošanai bieži tiek izmantotas dažādas formulas, piemēram, saīsinātās reizināšanas formulas, dažādu funkciju īpašības u.c.

Algebriskās izteiksmes.

Algebriskā izteiksme ir viens vai vairāki algebriski lielumi (skaitļi un burti), kas savstarpēji saistīti ar algebrisko darbību zīmēm: saskaitīšanu, atņemšanu, reizināšanu un dalīšanu, kā arī saknes izņemšanu un paaugstināšanu līdz veselam pakāpim (turklāt saknei un eksponentam obligāti jābūt ir veseli skaitļi) un šo darbību secības zīmes (parasti iekavas dažāda veida). Iekļauto daudzumu skaits algebriskā izteiksme jābūt galīgam.

Algebriskās izteiksmes piemērs:

"Algebriskā izteiksme" ir sintaktisks jēdziens, tas ir, kaut kas ir algebrisks izteiksme tad un tikai tad, ja tas atbilst noteiktiem gramatikas noteikumiem (skat. Formālā gramatika). Ja algebriskās izteiksmes burtus uzskata par mainīgajiem, tad algebriskā izteiksme iegūst algebriskās funkcijas nozīmi.

No plašā daudzveidības komplektiīpaši interesanti ir tā sauktie numuru komplekti, tas ir, kopas, kuru elementi ir skaitļi. Skaidrs, ka ērtam darbam ar viņiem ir jāprot tās pierakstīt. Mēs sāksim šo rakstu ar apzīmējumiem un ciparu kopu rakstīšanas principiem. Un tad mēs apsvērsim, kā skaitļu kopas tiek attēlotas uz koordinātu līnijas.

Lapas navigācija.

Ciparu kopu rakstīšana

Sāksim ar pieņemto apzīmējumu. Kā zināms, kopu apzīmēšanai tiek izmantoti latīņu alfabēta lielie burti. Ciparu kopas, piemēram īpašs gadījums kopas ir arī apzīmētas. Piemēram, var runāt par skaitļu kopām A , H , W u.c. Īpaši svarīgas ir dabisko, veselo skaitļu, racionālo, reālo, komplekso skaitļu utt. kopas, kurām tika pieņemti paši apzīmējumi:

• N ir visu naturālo skaitļu kopa;
• Z ir veselu skaitļu kopa;
• Q ir racionālo skaitļu kopa;
• J ir iracionālo skaitļu kopa;
• R ir reālo skaitļu kopa;
• C ir komplekso skaitļu kopa.

No tā ir skaidrs, ka kopu, kas sastāv, piemēram, no diviem skaitļiem 5 un -7, nav nepieciešams apzīmēt kā Q, šis apzīmējums būs maldinošs, jo burts Q parasti apzīmē visu racionālo skaitļu kopu. Lai apzīmētu norādīto ciparu kopu, labāk ir izmantot kādu citu "neitrālu" burtu, piemēram, A.

Tā kā mēs runājam par apzīmējumu, šeit mēs atgādinām arī tukšas kopas apzīmējumu, tas ir, kopu, kas nesatur elementus. To apzīmē ar zīmi ∅.

Atcerēsimies arī kopas elementa piederības un nepiederības apzīmējumu. Lai to izdarītu, izmantojiet zīmes ∈ - pieder un ∉ - nepieder. Piemēram, ieraksts 5∈N nozīmē, ka skaitlis 5 pieder naturālu skaitļu kopai, bet 5.7∉Z - decimāldaļdaļa 5.7 nepieder veselu skaitļu kopai.

Atcerēsimies arī apzīmējumu, kas pieņemts, lai iekļautu vienu kopu citā. Ir skaidrs, ka visi kopas N elementi ir iekļauti kopā Z, tādējādi, numuru komplekts N ir iekļauts Z , tas tiek apzīmēts kā N⊂Z . Var izmantot arī apzīmējumu Z⊃N , kas nozīmē, ka visu veselo skaitļu kopa Z ietver kopu N . Neiekļautās un neiekļautās attiecības tiek apzīmētas attiecīgi ar zīmēm ⊄ un . Tiek izmantotas arī formas ⊆ un ⊇ nestingrās iekļaušanas zīmes, kas nozīmē attiecīgi iekļauts vai atbilst un ietver vai atbilst.

Mēs runājām par apzīmējumu, pāriesim pie skaitlisko kopu apraksta. Šajā gadījumā mēs pieskarsimies tikai galvenajiem gadījumiem, kas visbiežāk tiek izmantoti praksē.

Sāksim ar skaitliskām kopām, kas satur ierobežotu un nelielu elementu skaitu. Skaitliskās kopas, kas sastāv no ierobežota elementu skaita, var ērti aprakstīt, uzskaitot visus to elementus. Visi skaitļu elementi ir rakstīti, atdalot tos ar komatiem un ievietoti , kas atbilst kopējam noteikt apraksta noteikumus. Piemēram, kopu, kas sastāv no trim skaitļiem 0 , -0,25 un 4/7, var aprakstīt kā (0, -0,25, 4/7) .

Dažkārt, kad skaitliskās kopas elementu skaits ir pietiekami liels, bet elementi pakļaujas kādam modelim, aprakstīšanai izmanto elipsi. Piemēram, visu nepāra skaitļu kopu no 3 līdz 99 ieskaitot var uzrakstīt kā (3, 5, 7, ..., 99) .

Tātad mēs gludi tuvojāmies skaitlisko kopu aprakstam, kuru elementu skaits ir bezgalīgs. Dažreiz tos var aprakstīt, izmantojot visu to pašu elipsi. Piemēram, aprakstīsim visu naturālo skaitļu kopu: N=(1, 2. 3, …) .

Viņi izmanto arī skaitlisko kopu aprakstu, norādot tā elementu īpašības. Šajā gadījumā tiek izmantots apzīmējums (x| īpašības). Piemēram, apzīmējums (n| 8 n+3, n∈N) definē tādu naturālu skaitļu kopu, kurus dalot ar 8, paliek 3. To pašu kopu var raksturot kā (11,19, 27, ...) .

Īpašos gadījumos skaitliskās kopas ar bezgalīgu elementu skaitu ir zināmas kopas N , Z , R u.c. vai skaitļu atstarpes. Un kopumā skaitliskās kopas tiek attēlotas kā asociācija atsevišķi skaitliskie intervāli, kas tos veido, un skaitliskās kopas ar ierobežotu elementu skaitu (par ko mēs runājām nedaudz augstāk).

Parādīsim piemēru. Lai skaitļu kopa ir skaitļi −10 , −9 , −8.56 , 0 , visi intervāla [−5, −1.3] skaitļi un atvērtā skaitļu stara (7, +∞) skaitļi. Pamatojoties uz kopu savienības definīciju, norādīto skaitlisko kopu var uzrakstīt kā {−10, −9, −8,56}∪[−5, −1,3]∪{0}∪(7, +∞) . Šāds apzīmējums faktiski nozīmē kopu, kas satur visus kopu elementus (−10, −9, −8.56, 0) , [−5, −1.3] un (7, +∞) .

Līdzīgi, kombinējot dažādus skaitliskos diapazonus un atsevišķu skaitļu kopas, var aprakstīt jebkuru skaitļu kopu (kas sastāv no reāliem skaitļiem). Šeit kļūst skaidrs, kāpēc tiek atvērti tādi skaitlisko intervālu veidi kā intervāls, pusintervāls, segments skaitļu stars un skaitļu stars: tie visi kopā ar atsevišķu skaitļu kopu apzīmējumiem ļauj aprakstīt jebkuras skaitļu kopas, izmantojot to savienojumu.

Lūdzu, ņemiet vērā, ka, rakstot skaitlisko kopu, tās veidojošie numuri un ciparu intervāli tiek sakārtoti augošā secībā. Tas nav obligāts, bet vēlams nosacījums, jo sakārtotu ciparu kopu ir vieglāk attēlot un attēlot uz koordinātu līnijas. Ņemiet vērā arī to, ka šādos ierakstos netiek izmantoti skaitļu intervāli ar kopīgi elementi, jo šādus ierakstus var aizstāt ar ciparu intervālu savienību bez kopīgiem elementiem. Piemēram, skaitlisko kopu savienība ar kopīgiem elementiem [−10, 0] un (−5, 3) ir pusintervāls [−10, 3) . Tas pats attiecas uz ciparu intervālu savienību ar vienādiem robežskaitļiem, piemēram, savienība (3, 5]∪(5, 7] ir kopa (3, 7] ), mēs pie tā pakavēsimies atsevišķi, kad iemācīsimies atrast skaitļu kopu krustpunktu un savienību.

Skaitļu kopu attēls uz koordinātu līnijas

Praksē ir ērti izmantot skaitlisko kopu ģeometriskos attēlus - to attēlus uz . Piemēram, kad nevienlīdzību risināšana, kurā jāņem vērā ODZ, ir jāattēlo ciparu kopas, lai atrastu to krustpunktu un/vai savienību. Tātad būs noderīgi labi izprast visas skaitļu kopu attēlojuma nianses koordinātu taisnē.

Ir zināms, ka starp koordinātu līnijas punktiem un reālajiem skaitļiem ir atbilstība viens pret vienu, kas nozīmē, ka pati koordinātu līnija ir visu reālo skaitļu kopas R ģeometriskais modelis. Tātad, lai attēlotu visu reālo skaitļu kopu, ir jānozīmē koordinātu līnija ar izšķilšanos visā tās garumā:

Un bieži vien tie pat nenorāda izcelsmi un vienu segmentu:

Tagad parunāsim par skaitlisko kopu attēlu, kas ir daži ierobežoti atsevišķi skaitļi. Piemēram, uzzīmēsim skaitļu kopu (−2, −0.5, 1.2) . Šīs kopas ģeometriskais attēls, kas sastāv no trim skaitļiem -2, -0,5 un 1,2, būs trīs koordinātu līnijas punkti ar atbilstošām koordinātām:

Ņemiet vērā, ka parasti prakses vajadzībām nav nepieciešams precīzi veikt zīmējumu. Bieži vien pietiek ar shematisku zīmējumu, kas nozīmē, ka nav nepieciešams saglabāt mērogu, bet ir svarīgi tikai saglabāt savstarpēja vienošanās punkti viens pret otru: jebkuram punktam ar mazāku koordinātu jāatrodas pa kreisi no punkta ar lielāku koordinātu. Iepriekšējais zīmējums shematiski izskatīsies šādi:

Atsevišķi no visām iespējamām skaitliskām kopām izšķir skaitliskos intervālus (intervālus, pusintervālus, starus u.c.), kas attēlo to ģeometriskos attēlus, sīkāk apskatījām sadaļā. Mēs šeit neatkārtosimies.

Un atliek tikai pakavēties pie skaitļu kopu attēla, kas ir vairāku skaitlisko intervālu un kopu, kas sastāv no atsevišķiem skaitļiem, savienība. Šeit nav nekā sarežģīta: saskaņā ar savienības nozīmi šajos gadījumos uz koordinātu līnijas ir jāattēlo visas dotās skaitliskās kopas kopas sastāvdaļas. Kā piemēru parādīsim skaitļu kopas attēlu (−∞, −15)∪{−10}∪[−3,1)∪ (log 2 5, 5)∪(17, +∞) :

Un pakavēsimies pie diezgan izplatītiem gadījumiem, kad attēlotā skaitliskā kopa ir visa reālo skaitļu kopa, izņemot vienu vai vairākus punktus. Šādas kopas bieži nosaka tādi nosacījumi kā x≠5 vai x≠−1, x≠2, x≠3,7 utt. Šajos gadījumos ģeometriski tie attēlo visu koordinātu līniju, izņemot atbilstošos punktus. Citiem vārdiem sakot, šie punkti ir "jāizsit" no koordinātu līnijas. Tie ir attēloti kā apļi ar tukšu centru. Skaidrības labad uzzīmēsim skaitļu kopu, nosacījumiem (šis komplekts būtībā ir):

Apkopojiet. Ideālā gadījumā iepriekšējo rindkopu informācijai būtu jāveido tāds pats skaitļu kopu ierakstīšanas un attēlojuma skats kā atsevišķu skaitlisko intervālu skatam: skaitļu kopas ierakstam nekavējoties jāsniedz tās attēls uz koordinātu līnijas, bet no attēla tālāk. koordinātu līniju, mums jābūt gataviem viegli aprakstīt atbilstošo skaitļu kopu, izmantojot atsevišķu atstarpju un kopu, kas sastāv no atsevišķiem skaitļiem, savienību.

Bibliogrāfija.

• Algebra: mācību grāmata 8 šūnām. vispārējā izglītība iestādes / [Yu. N. Makaričevs, N. G. Mindjuks, K. I. Neškovs, S. B. Suvorova]; ed. S. A. Teļakovskis. - 16. izd. - M. : Izglītība, 2008. - 271 lpp. : slim. - ISBN 978-5-09-019243-9.
• Mordkovičs A.G. Algebra. 9. klase Plkst.14 1.daļa Skolēna mācību grāmata izglītības iestādēm/ A. G. Mordkovičs, P. V. Semenovs. - 13. izd., Sr. - M.: Mnemosyne, 2011. - 222 lpp.: ill. ISBN 978-5-346-01752-3.

Veidojiet skaitļus

Digitālajās ierīcēs ir divu veidu skaitļu attēli: ar fiksētu і peldošā koma.

Priekšējā rindkopā bija redzami tikai daži pozitīvi skaitļi. Formula (1.14) dod iespēju parādīt dubultskaitli ar veselu un daļskaitli un fiksētu komu. Divciparu skaitļa zīmi ar fiksētu komu piešķir papildu pakāpe, kas tiek novietota skaitļu priekšā. Papildu skaitļiem papildu pasūtījuma vērtība ir vienāda 0 ”, vizuālajiem materiāliem - “ 1 ”.

Pie galda 1.3 ir trīs iespējas kodēt pēdējo un otro numuru ar dubulto kodu.

1.3. tabula.

Pirmajā variantā, kā izrādās no tabulām, kodētajā dubultā secībā var būt papildu un beigu nulles vieta, kas var radīt problēmas ar aritmētisko darbību parādīšanos.

Doto skaitļu attēlojums vārtu kodā arī neatrisina augstāk minēto problēmu. Jūs nekļūdīsities tikai vienu reizi, ja redzat skaitļus papildu kods, ko aprēķina pēc formulas:

Uz att. 1.12 parāda pozitīvo un negatīvo skaitļu attēla grafisku interpretāciju, kas ir līdzīgi nullei tiešo un papildinošo kodu alternatīvām. Kā tiks parādīts vēlāk, šāda desmito skaitļu attēlojuma forma vienkārši vienkāršos aritmētiskās darbības.

Piemērs 1.10. Zināt papildkodu desmitajiem skaitļiem: 0 10 , 17 10 , -127 10 .

Rozvjazanņa. Mēs zinām divus doto skaitļu ekvivalentus:

0 10 = 00000000 2 ; 17 10 = 00010001 2 ; -127 10 = 10000001 2 .

Mēs zinām kodu, zvorotnі dvіykovim - vіdpovіdno: 11111111; 11101110; 01111110.

Ir zināms, ka doto skaitļu kodus var papildināt: 11111111 + 1 = 100000000 2 = 0 10;

11101110 + 1 = 11101111 2 = -17 10 ; 01111110 + 1 = 01111111 2 = 127 10 .

Tagad mēs izskaidrojam skaitļu ierakstīšanas būtību ar fiksētu komu. Neatkarīgi no tā, vai numuru digitālajās sistēmās aizņem īpašas atmiņas ierīces, no noteikta elementu skaita tiek izveidota apvalku rinda. Koma, kas šāvienu skaitā iekļāva daļu no šāvienu skaita, atmiņas rindā ieņem fiksētu pozīciju - vecākā ranga priekšā vai pēc jaunā.

Pirmajam tipam skaitļa absolūtā vērtība ir mazāka par vienu - piemēram, 0,110101 2 . 1.13, galīgajā leviy rangā tiek parādīta skaitļa zīme, bet reshta - moduļa rangs. Viļņu jauniešu izplūdes ir piepildītas ar nullēm. Oskіlki pārskatītajā vipadku rindā atmiņa tiek pārsūtīta, lai ierakstītu tikai daļēju skaitļa daļu, tad visu darbību rezultāti ir saistīti ar absolūtajām vērtībām, kas ir mazākas par vienu. Wikonnannya tsієї noteikti izvēlieties atbilstošos mēroga faktorus, uz kuriem tiek reizināti ārējie dati. Ja vibrāciju skalas koeficients ir nepareizs, tad var notikt izlāžu pārkārtošanās un visas daļas izskats, it kā tā tiks iztērēta, izlādes režģī esošās lauskas netiks pārnestas uz її izskatu. Tomēr es jūs novedu ellē ar rezultātu, kuram trūkst šādas metodes.

Citā noskaņojumā, ja koma ir fiksēta pēc jaunākā pasūtījuma, tas var būt pareizi ar veseliem skaitļiem. Tā, piemēram, skaitlis 10011 2 atmiņas rindā tiek ievietots attēla redzamībā. 1.14, de livy rangs ir zīme, un, sekojot tai labajā pusē, brīvie cipari ir aizpildīti ar nullēm. Tādā veidā moduļa vērtība ir iežogota atmiņas rinda.

Skaitļi ar peldošu komu pārnes skaitļa attēlu uz dievlūdzēju variantu, kas tiek reizināts ar skaitļu sistēmas bāzi stadijā, kas ir sakārtota. Piemēram, skaitlis 200 ir rakstīts kā 0,2 × 10 3, bet skaitlis 0,000312 - kā 0,312 × 10 -3. Vidpovidno zapisyutsya un dvіykovі numuri. Mantis un pasūtījums tiek parādīti dubultā kodā, un pamatā ir divi. Piemēram, skaitlis 0,111 × 2 10 \u003d 11,10 2 desmitajā sistēmā tiek parādīts kā 0,875 × 2 2 \u003d 3,5 10. Atmiņas rindā šādi skaitļi tiek ņemti no divām skaitļu grupām: pirmā grupa - dievlūdzējs - nosaka pašu skaitli, otra - secību - komi vietu skaitļā (1.15. att.).

Pie atmiņas rindas nulles elementa tiek parādīta skaitļa zīme (dotajam dubultskaitlim, kas ierakstīts atmiņas rindā - “ 0 ”). Attālumi tiek iestatīti skaitļu secībā (stowpts 1…8). Ja to dod mazāks rindu skaits, tad skaitļa labajā pusē esošie atmiņas elementi tiek aizpildīti ar nullēm. Devītajā kārtībā tiek parādīta pasūtījuma zīme, bet pēc analoģijas ar mantisu - skaitlis, kas apzīmē pasūtījumu. Ar šādu ierakstu skaitļa vērtība tiek iestatīta tā, lai dievlūdzēja pirmais nozīmīgais cipars nebūtu vienāds 0 ". Šo ieraksta veidu sauc normāli.

Minimālo papildu skaitli, ko var ierakstīt parastā formā atmiņas rindā, nosaka minimālā mantisa 0,1000..0 2 un maksimālā vizuālā secība 111..1 2 . Ar daudzumu k secībā no minimālā desmit pierakstāmo skaitli nosaka pēc formulas:

. (1.15)

Maksimālais matimemo skaits pie maksimālās dievlūdzēju vērtības (0,111 ... 1) 2 un maksimālais papildu pasūtījums (111 ... 1 2) = 2 k- 1, tad

Diapazons D skaitļi, kas attēloti normālā formā, kā izriet no formulām (1.15) un (1.16), apzīmē tikai skaitli k. Piemēram, priekš k= 6 ir zināms:

; .

Numura ierakstīšanas precizitāti nosaka pasūtījumu skaits m mantici. Ja skaitļa rindu skaits apvērš mantiņā ievadīto kārtu skaitu, tad skaitlis tiek noapaļots līdz vajadzīgajam skaitlim. Noteikums divu skaitļu noapaļošanai šādā veidā ir šāds: ja redzamās vārda daļas vecākā secība ir viena, tad vienu pievieno jaunākajai dievlūdzēja secībai. Ar šādu noapaļotu absolūto skaitli mantija attēls nepārsniedz pusi no jauno dievlūdzēju kategorijas koeficienta, kas tiek ņemts, tobto:

Vrakhovuchi, ka parastajā dievlūdzēja ieraksta formā nevar būt mazāks par 0,5, acīmredzama kļūda η:

Piemēram, kad m= 24 maєmo:

.

Mūsdienu digitālajās sistēmās skaitļu attēlošanai ar peldošu komu tiek izmantota dozhinoy chotiri baitu rinda. Ar 23 izlādi iestatiet dievlūdzēju, bet 7 - pasūtījuma lielumu. Parādāmo skaitļu diapazons ir salocīts no ± 2 127 līdz ± 2–127.

Ciparu variācijas ar peldošu komu paplašinās un vienkāršos skaitļu attēlojumu, taču operāciju daudzpusība ar šādiem skaitļiem ir vairāk sadarbības, zemāka skaitļiem ar fiksētu komu.

Racionālo skaitļu sistēmas izteiksmīgu ģeometrisko attēlojumu var iegūt šādi.

Rīsi. 8. Skaitļa ass

Uz kādas taisnes, "skaitliskās ass", mēs atzīmējam segmentu no 0 līdz 1 (8. att.). Tas nosaka vienības segmenta garumu, ko, vispārīgi runājot, var izvēlēties patvaļīgi. Pēc tam pozitīvie un negatīvie veselie skaitļi tiek attēloti kā vienādi izvietotu punktu kopa uz skaitļa ass, proti, pozitīvie skaitļi ir atzīmēti pa labi, bet negatīvie - pa kreisi no punkta 0. Lai attēlotu skaitļus ar saucēju, mēs sadalām katru. no iegūtajiem vienības garuma segmentiem vienādās daļās; dalīšanas punkti attēlos daļskaitļus ar saucēju. Ja to darīsim vērtībām, kas atbilst visiem naturālajiem skaitļiem, tad katrs racionālais skaitlis tiks attēlots ar kādu punktu uz skaitliskās ass. Mēs piekritīsim šos punktus saukt par "racionāliem"; kopumā termini "racionālais skaitlis" un "racionālais punkts" tiks izmantoti kā sinonīmi.

I nodaļas 1. punktā tika definēta naturālo skaitļu nevienlīdzības attiecība. Uz skaitļu ass šī attiecība tiek atspoguļota šādi: ja dabiskais skaitlis A ir mazāks par naturālu skaitli B, tad punkts A atrodas pa kreisi no punkta B. Tā kā norādītā ģeometriskā sakarība ir noteikta jebkuram racionālu punktu pārim, ir dabiski mēģināt vispārināt aritmētisko nevienādības attiecību šādā veids, kā saglabāt šo ģeometrisko secību aplūkotajiem punktiem. Tas ir iespējams, ja pieņemam šādu definīciju: mēs sakām, ka racionālais skaitlis A ir mazāks par racionāls skaitlis vai arī skaitlis B ir lielāks par skaitli, ja starpība ir pozitīva. No šī (par ) izriet, ka punkti (skaitļi) starp ir tie, kas

vienlaicīgi Katrs šāds punktu pāris kopā ar visiem punktiem starp tiem tiek saukts par segmentu (vai segmentu) un tiek apzīmēts (un tikai starppunktu kopu sauc par intervālu (vai intervālu), ko apzīmē ar

Patvaļīga punkta A attālumu no sākuma 0, ko uzskata par pozitīvu skaitli, sauc par A absolūto vērtību un apzīmē ar simbolu

Jēdziens "absolūtā vērtība" tiek definēts šādi: ja , tad ja tad Ir skaidrs, ka, ja skaitļiem ir vienāda zīme, tad vienlīdzība ir patiesa, ja tiem ir dažādas zīmes, tad. Apvienojot šos divus rezultātus kopā, mēs nonākam pie vispārējās nevienlīdzības

kas ir spēkā neatkarīgi no zīmēm

Fundamentāli svarīgu faktu izsaka šāds apgalvojums: racionālie punkti visur ir blīvi uz skaitļu līnijas. Šī apgalvojuma nozīme ir tāda, ka jebkurā intervālā, lai cik mazs tas būtu, ir racionāli punkti. Lai pārbaudītu norādītā apgalvojuma derīgumu, pietiek ņemt tik lielu skaitli, lai intervāls ( būs mazāks par doto intervālu ; tad vismaz viens no formas punktiem atradīsies šajā intervālā. Tātad ir uz skaitļu ass nav tāda intervāla (pat mazākā, ko var iedomāties), kurā nebūtu racionālu punktu. No tā izriet tālāka secība: katrs intervāls satur bezgalīgu skaitu racionālu punktu. Patiešām, ja kāds intervāls saturētu tikai ierobežots skaits racionālu punktu, tad intervālā, ko veido divi blakus esošie šādi punkti, vairs nebūtu racionālu punktu, un tas ir pretrunā ar tikko pierādīto.