Propriétés des angles opposés d'un parallélogramme. Propriété des diagonales d'un parallélogramme

Signes de pa-ral-le-lo-gram-ma

1. Définition et propriétés de base d'un parallélogramme

Commençons par le fait que nous nous souvenons de la définition de pa-ral-le-lo-gram-ma.

Définition. Parallélogramme- quatre-vous-rekh-coal-nick, quelqu'un-ro-go a deux côtés pro-ti-in-on-faux de para-ral-lel-ny (voir Fig. . un).

Riz. 1. Pa-ral-le-lo-gramme

Rappeler nouvelles propriétés fondamentales de pa-ral-le-lo-gram-ma:

Pour pouvoir utiliser toutes ces propriétés, vous devez être sûr que fi-gu-ra, oh quelqu'un -Roy Dans la question, - pa-ral-le-lo-gramme. Pour cela, il est nécessaire de connaître des faits tels que les signes de pa-ral-le-lo-gram-ma. Les deux premiers d'entre eux que nous examinons aujourd'hui.

2. Le premier signe d'un parallélogramme

Théorème. Le premier signe de pa-ral-le-lo-gram-ma. Si dans quatre-vous-rekh-charbon-ni-ke deux côtés pro-ti-en-faux sont égaux et par-ral-lel-na, alors ce surnom de quatre-vous-rekh-charbon - parallélogramme. .

Riz. 2. Le premier signe de pa-ral-le-lo-gram-ma

Preuve. We-we-we-dem in four-rekh-coal-ni-ke dia-go-nal (voir Fig. 2), elle l'a divisé en deux triangles-no-ka. Écrivez ce que nous savons de ces triangles :

selon le premier signe de l'égalité des triangles.

De l'égalité des triangles indiqués, il résulte que, selon le signe du par-ral-lel-no-sti des droites quand re-re-se-che-ni leur se-ku-schey. Nous avons ça :

Avant-pour-mais.

3. Le deuxième signe d'un parallélogramme

Théorème. Le deuxième essaim est un signe de pa-ral-le-lo-gram-ma. Si dans quatre-vous-rekh-coal-ni-ke, tous les deux côtés pro-ti-en-faux sont égaux, alors ce quatre-vous-rekh-coal-nick - parallélogramme. .

Riz. 3. Deuxième signe d'essaim pa-ral-le-lo-gram-ma

Preuve. We-we-we-dem in four-you-rekh-coal-ni-ke dia-go-nal (voir Fig. 3), elle le divise en deux triangles-no-ka. Nous écrivons ce que nous savons de ces triangles, en partant de la théorie for-mu-li-ditch-ki theo-re-we :

selon le troisième signe de l'égalité des triangles.

De l'égalité des triangles, il s'ensuit que, selon le signe du par-ral-lel-no-sti des lignes droites lors de leur re-se-che-ing se-ku-schey. Par-lu-cha-eat :

pa-ral-le-lo-gramme selon la définition-de-le-ny. Q.E.D.

Avant-pour-mais.

4. Un exemple d'utilisation de la première caractéristique d'un parallélogramme

Ras-regardez un exemple d'application des signes de pa-ral-le-lo-gram-ma.

Exemple 1. Dans you-far-scrap-che-you-rex-coal-no-ke Trouver : a) les coins de quatre-you-rex-coal-no-ka ; b) cent puits.

Décision. Image-ra-hiver Fig. 4.

pa-ral-le-lo-gram selon le premier signe-ku pa-ral-le-lo-gram-ma.

MAIS. selon la propriété de para-le-lo-gram-ma sur les pro-ti-en-faux-angles, selon la propriété de para-le-lo-gram-ma sur la somme des angles, at- couché à un côté.

B par la propriété d'égalité des pro-ty-in-on-faux côtés.

re-at-sign pa-ral-le-lo-gram-ma

5. Répétition : définition et propriétés d'un parallélogramme

Rappel que parallélogramme- c'est un four-you-rekh-coal-nick, quelqu'un a un pro-ti-in-on-faux côtés dans une paire-mais-pa-ral-lel-na. Autrement dit, si - pa-ral-le-lo-gram, alors (Voir Fig. 1).

Pa-ral-le-lo-gramme possède toute une gamme de propriétés : pro-ti-en-sur-faux les angles sont égaux (), pro-ti-en-sur-faux cent-ro -we sont égaux ( ). De plus, dia-go-on-si par-ral-le-lo-gram-ma au point de re-se-che-niya de-lyat-by-lam, la somme des angles, at-le- pa-ral-le-lo-gram-ma, égal à n'importe quel côté, égal, etc.

Mais pour utiliser toutes ces propriétés, il faut être ab-so-lu-mais-sûr-nous que les races ri-va-e-my che-you-rekh-coal-nick - pa-ral-le- lo-gramme. Pour cela, et so-s-stu-stu-ut-signs-pa-ral-le-lo-gram-ma: c'est-à-dire ces faits à partir desquels on peut tirer une conclusion à valeur unique , que che-you-rekh -coal-nick yav-la-et-sya pa-ral-le-lo-gram-maman. Dans la leçon précédente, nous avons déjà considéré deux signes. Cette heure, nous regardons le troisième.

6. La troisième caractéristique d'un parallélogramme et sa preuve

Si dans quatre-vous-rekh-coal-ni-ke dia-go-na-li au point de re-se-che-niya de-lyat-by-lam, alors ce quatre-vous-reh-coal-nick yav-la-et-sya pa-ral-le-lo-gram-maman.

Donné:

Che-vous-reh-charbon-nick ; ; .

Prouver:

Parallélogramme.

Preuve:

Afin de prouver ce fait, il est nécessaire de prouver la para-ral-lel-ness des côtés du pa-ral-le-lo-gram-ma. Et la par-ral-lel-ness des lignes droites est le plus souvent jusqu'à-ka-zy-va-et-sya grâce à l'égalité des angles internes à croisés de la croix au niveau de ces lignes droites. De cette façon, na-pra-shi-va-et-sya la voie suivante-du-u-sche vers-ka-pour-tel-stva du troisième signe-de-pa-ral -le-lo-gram- ma : par l'égalité des triangles-ni-kov .

Attendons l'égalité de ces triangles. En effet, de la condition suit :. De plus, comme les angles sont verticaux, ils sont égaux. C'est à dire:

(premier signe d'égalitétriangulaire-ni-kov- deux cents ro-us et l'angle entre eux).

De l'égalité des triangles: (puisque les angles internes sur la croix sont égaux à ces lignes droites et se-ku-schey). De plus, de l'égalité des triangles, il résulte que. Cela signifie que nous sommes, comme, chi-li, que dans four-you-rekh-coal-ni-ke, deux côtés sont égaux et par-ral-lel-na. Selon le premier signe, pa-ral-le-lo-gram-ma : - pa-ral-le-lo-gram.

Avant-pour-mais.

7. Un exemple de problème sur la troisième caractéristique d'un parallélogramme et généralisation

Ras-regardez un exemple d'application du troisième signe du para-ral-le-lo-gram-ma.

Exemple 1

Donné:

- parallélogramme; . - se-re-di-na, - se-re-di-na, - se-re-di-na, - se-re-di-na (voir Fig. 2).

Prouver:- pa-ral-le-lo-gramme.

Preuve:

Ainsi, dans quatre-vous-rekh-charbon-no-ke dia-go-na-li au point de re-se-che-niya de-lyat-sya-by-lam. D'après le troisième signe, pa-ral-le-lo-gram-ma, il en résulte que - pa-ral-le-lo-gram.

Avant-pour-mais.

Si nous analysons le troisième signe du pa-ral-le-lo-gram-ma, alors nous pouvons remarquer que ce signe est co-ot-reply- a la propriété de par-ral-le-lo-gram-ma. C'est-à-dire que le fait que dia-go-na-qu'ils dé-lyat-by-lam, is-la-et-sya ne soit pas seulement une propriété de pa-ral-le-lo-gram-ma, et cela vient de -li-chi-tel-nym, propriété ha-rak-te-ri-sti-che-sky, selon certains-ro-mu, il peut être déversé d'une multitude che-you-reh-charbon-no- cov.

LA SOURCE

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://www.tepka.ru/geometriya/16.1.gif

Dans la leçon d'aujourd'hui, nous répéterons les principales propriétés d'un parallélogramme, puis nous prêterons attention à la considération des deux premières caractéristiques d'un parallélogramme et les prouverons. Au cours de la démonstration, rappelons l'application des signes d'égalité des triangles, que nous avons étudiée l'année dernière et répétée dans la première leçon. A la fin, un exemple sera donné sur l'application des caractéristiques étudiées d'un parallélogramme.

Thème : Quadrilatères

Leçon : Signes d'un parallélogramme

Commençons par rappeler la définition d'un parallélogramme.

Définition. Parallélogramme- un quadrilatère dans lequel tous les deux côtés opposés sont parallèles (voir Fig. 1).

Riz. 1. Parallélogramme

Souvenons-nous propriétés de base d'un parallélogramme:

Pour pouvoir utiliser toutes ces propriétés, vous devez être sûr que la figure en question est un parallélogramme. Pour ce faire, vous devez connaître des faits tels que les signes d'un parallélogramme. Nous examinerons les deux premiers d'entre eux aujourd'hui.

Théorème. La première caractéristique d'un parallélogramme. Si dans un quadrilatère deux côtés opposés sont égaux et parallèles, alors ce quadrilatère est parallélogramme. .

Riz. 2. Le premier signe d'un parallélogramme

Preuve. Traçons une diagonale dans le quadrilatère (voir Fig. 2), elle l'a divisé en deux triangles. Écrivons ce que nous savons de ces triangles :

selon le premier signe d'égalité des triangles.

De l'égalité de ces triangles il résulte que, sur la base du parallélisme des droites à l'intersection de leur sécante. Nous avons ça :

Éprouvé.

Théorème. Le deuxième signe d'un parallélogramme. Si dans un quadrilatère tous les deux côtés opposés sont égaux, alors ce quadrilatère est parallélogramme. .

Riz. 3. Le deuxième signe d'un parallélogramme

Preuve. Traçons une diagonale dans le quadrilatère (voir Fig. 3), elle le divise en deux triangles. Écrivons ce que nous savons de ces triangles, basé sur la formulation du théorème :

selon le troisième critère d'égalité des triangles.

De l'égalité des triangles découle celle du parallélisme des droites à l'intersection de leur sécante. On a:

parallélogramme par définition. Q.E.D.

Éprouvé.

Considérons un exemple d'application des caractéristiques d'un parallélogramme.

Exemple 1. Dans un quadrilatère convexe Trouver : a) les coins du quadrilatère ; b) côté.

Décision. Représentons la Fig. 4.

Riz. 4

parallélogramme selon le premier attribut d'un parallélogramme.

Le concept de parallélogramme

Définition 1

Parallélogramme est un quadrilatère dont les côtés opposés sont parallèles entre eux (Fig. 1).

Image 1.

Un parallélogramme a deux propriétés principales. Considérons-les sans preuve.

Propriété 1 : Les côtés opposés et les angles d'un parallélogramme sont respectivement égaux.

Propriété 2 : Les diagonales tracées dans un parallélogramme sont bissectées par leur point d'intersection.

Caractéristiques du parallélogramme

Considérez trois caractéristiques d'un parallélogramme et présentez-les sous forme de théorèmes.

Théorème 1

Si les deux côtés d'un quadrilatère sont égaux et également parallèles, alors ce quadrilatère sera un parallélogramme.

Preuve.

Donnons-nous un quadrilatère $ABCD$. Où $AB||CD$ et $AB=CD$ Traçons-y une diagonale $AC$ (Fig. 2).

Figure 2.

Considérons les droites parallèles $AB$ et $CD$ et leur sécante $AC$. Puis

\[\angle CAB=\angle DCA\]

comme des coins transversaux.

D'après le critère $I$ d'égalité des triangles,

puisque $AC$ est leur côté commun, et $AB=CD$ par hypothèse. Moyens

\[\angle CAD=\angle ACB\]

Considérons les droites $AD$ et $CB$ et leur sécante $AC$ ; par la dernière égalité des angles croisés, on obtient que $AD||CB$.) Donc, par définition de $1$, ce quadrilatère est un parallélogramme.

Le théorème a été prouvé.

Théorème 2

Si les côtés opposés d'un quadrilatère sont égaux, alors c'est un parallélogramme.

Preuve.

Donnons-nous un quadrilatère $ABCD$. Où $AD=BC$ et $AB=CD$. Traçons-y une diagonale $AC$ (Fig. 3).

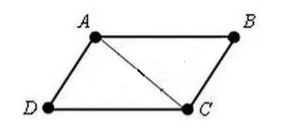
figure 3

Puisque $AD=BC$, $AB=CD$ et $AC$ est un côté commun, alors par le test d'égalité du triangle $III$,

\[\triangle DAC=\triangle ACB\]

\[\angle CAD=\angle ACB\]

Considérons les droites $AD$ et $CB$ et leur sécante $AC$, par la dernière égalité des angles croisés on obtient que $AD||CB$. Donc, par définition de $1$, ce quadrilatère est un parallélogramme.

\[\angle DCA=\angle CAB\]

Considérons les droites $AB$ et $CD$ et leur sécante $AC$, par la dernière égalité des angles croisés on obtient que $AB||CD$. Donc, d'après la définition 1, ce quadrilatère est un parallélogramme.

Le théorème a été prouvé.

Théorème 3

Si les diagonales tracées dans un quadrilatère sont divisées en deux parties égales par leur point d'intersection, alors ce quadrilatère est un parallélogramme.

Preuve.

Donnons-nous un quadrilatère $ABCD$. Traçons-y les diagonales $AC$ et $BD$. Laissez-les se croiser au point $O$ (Fig. 4).

Figure 4

Puisque, par la condition $BO=OD,\ AO=OC$, et les angles $\angle COB=\angle DOA$ sont verticaux, alors, par le test d'égalité du triangle $I$,

\[\triangle BOC=\triangle AOD\]

\[\angle DBC=\angle BDA\]

Considérons les droites $BC$ et $AD$ et leur sécante $BD$, par la dernière égalité des angles croisés on obtient que $BC||AD$. Aussi $BC=AD$. Donc, d'après le théorème $1$, ce quadrilatère est un parallélogramme.

Un parallélogramme est un quadrilatère dont les côtés opposés sont deux à deux parallèles. La figure suivante montre parallélogramme ABCD. Il a le côté AB parallèle au côté CD et le côté BC parallèle au côté AD.

Comme vous l'avez peut-être deviné, un parallélogramme est un quadrilatère convexe. Considérez les propriétés de base d'un parallélogramme.

Propriétés du parallélogramme

1. Dans un parallélogramme, les angles opposés et les côtés opposés sont égaux. Prouvons cette propriété - considérons le parallélogramme illustré dans la figure suivante.

Diagonal BD le divise en deux triangle égal: ABD et CBD. Ils sont égaux du côté BD et de deux angles qui lui sont adjacents, puisque les angles situés à la sécante de BD sont respectivement des droites parallèles BC et AD et AB et CD. Donc, AB = CD et
BC=AD. Et de l'égalité des angles 1, 2, 3 et 4, il s'ensuit que angle A = angle1 + angle3 = angle2 + angle4 = angle C.

2. Les diagonales du parallélogramme sont bissectées par le point d'intersection. Soit le point O le point d'intersection des diagonales AC et BD du parallélogramme ABCD.

Alors le triangle AOB et le triangle COD sont égaux entre eux, le long du côté et de deux angles qui lui sont adjacents. (AB = CD car ce sont des côtés opposés du parallélogramme. Et angle1 = angle2 et angle3 = angle4 comme angles croisés à l'intersection des lignes AB et CD par les sécantes AC et BD, respectivement.) Il s'ensuit que AO = OC et OB = OD, qui devait être prouvé.

Toutes les propriétés principales sont illustrées dans les trois figures suivantes.

Notes IMPORTANTES!
1. Si au lieu de formules vous voyez abracadabra, videz votre cache. Comment le faire dans votre navigateur est écrit ici:
2. Avant de commencer à lire l'article, faites attention à notre navigateur pour le plus ressource utile pour

1. Parallélogramme

Mot composé "parallélogramme" ? Et derrière c'est une figure très simple.

Eh bien, c'est-à-dire que nous avons pris deux lignes parallèles:

Traversé par deux autres :

Et à l'intérieur - un parallélogramme !

Quelles sont les propriétés d'un parallélogramme ?

Propriétés du parallélogramme.

Autrement dit, que peut-on utiliser si un parallélogramme est donné dans le problème ?

Cette question est répondue par le théorème suivant :

Dessinons tout en détail.

Que signifie premier point du théorème? Et le fait que si vous AVEZ un parallélogramme, alors par tous les moyens

Le deuxième paragraphe signifie que s'il y a un parallélogramme, alors, encore une fois, par tous les moyens :

Eh bien, et enfin, le troisième point signifie que si vous AVEZ un parallélogramme, alors assurez-vous :

Voyez quelle richesse de choix? Quoi utiliser dans la tâche ? Essayez de vous concentrer sur la question de la tâche, ou essayez tout à tour de rôle - une sorte de «clé» fera l'affaire.

Et maintenant posons-nous une autre question : comment reconnaître un parallélogramme « en face » ? Que doit-il advenir d'un quadrilatère pour qu'on ait le droit de lui donner le « titre » de parallélogramme ?

Cette question est répondue par plusieurs signes d'un parallélogramme.

Caractéristiques d'un parallélogramme.

Attention! Commencer.

Parallélogramme.

Attention : si vous avez trouvé au moins un signe dans votre problème, alors vous avez exactement un parallélogramme, et vous pouvez utiliser toutes les propriétés d'un parallélogramme.

2. Rectangle

Je ne pense pas que ce sera une nouvelle pour vous.

La première question est : un rectangle est-il un parallélogramme ?

Bien sûr que ça l'est ! Après tout, il a - rappelez-vous, notre signe 3 ?

Et à partir de là, bien sûr, il s'ensuit que pour un rectangle, comme pour tout parallélogramme, et, et les diagonales sont divisées par le point d'intersection en deux.

Mais il y a un rectangle et une propriété distinctive.

Propriété Rectangle

Pourquoi cette propriété est-elle particulière ? Parce qu'aucun autre parallélogramme n'a de diagonales égales. Formulons-le plus clairement.

Attention : pour devenir un rectangle, un quadrilatère doit d'abord devenir un parallélogramme, puis présenter l'égalité des diagonales.

3. Diamant

Et encore une fois la question est : un losange est-il un parallélogramme ou non ?

Avec plein droit - un parallélogramme, car il a et (rappelez-vous notre signe 2).

Et encore une fois, puisqu'un losange est un parallélogramme, alors il doit avoir toutes les propriétés d'un parallélogramme. Cela signifie qu'un losange a des angles opposés égaux, les côtés opposés sont parallèles et les diagonales sont bissectées par le point d'intersection.

Propriétés du losange

Regarde l'image:

Comme dans le cas d'un rectangle, ces propriétés sont distinctives, c'est-à-dire que pour chacune de ces propriétés, nous pouvons conclure que nous avons non seulement un parallélogramme, mais un losange.

Signes d'un losange

Et faites encore attention : il ne devrait pas y avoir qu'un quadrilatère avec des diagonales perpendiculaires, mais un parallélogramme. S'assurer:

Non, bien sûr que non, bien que ses diagonales et soient perpendiculaires, et que la diagonale soit la bissectrice des angles u. Mais ... les diagonales ne se divisent pas, le point d'intersection en deux, donc - PAS un parallélogramme, et donc PAS un losange.

Autrement dit, un carré est à la fois un rectangle et un losange. Voyons ce qui en ressort.

Est-ce clair pourquoi? - losange - la bissectrice de l'angle A, qui est égale à. Donc, il se divise (et aussi) en deux angles le long.

Eh bien, c'est assez clair : les diagonales du rectangle sont égales ; les diagonales de losange sont perpendiculaires et, en général, les diagonales de parallélogramme sont divisées par le point d'intersection en deux.

NIVEAU MOYEN

Propriétés des quadrilatères. Parallélogramme

Propriétés du parallélogramme

Attention! Les mots " propriétés du parallélogramme» signifie que si vous avez une tâche il y a parallélogramme, alors tous les éléments suivants peuvent être utilisés.

Théorème sur les propriétés d'un parallélogramme.

Dans tout parallélogramme :

Voyons pourquoi c'est vrai, en d'autres termes NOUS PROUVERONS théorème.

Alors pourquoi 1) est-il vrai ?

Puisqu'il s'agit d'un parallélogramme, alors :

• comme couché en travers
• comme couché en travers.

Par conséquent, (sur la base II : et - général.)

Eh bien, une fois, alors - c'est tout! - prouvé.

Mais au fait ! Nous avons également prouvé 2) !

Pourquoi? Mais après tout (regardez la photo), c'est-à-dire parce que.

Il en reste 3).

Pour ce faire, il vous reste à tracer une seconde diagonale.

Et maintenant, nous voyons cela - selon le signe II (l'angle et le côté "entre" eux).

Propriétés éprouvées ! Passons aux signes.

Caractéristiques du parallélogramme

Rappelons que le signe d'un parallélogramme répond à la question "comment savoir ?" Que la figure est un parallélogramme.

Dans les icônes c'est comme ça :

Pourquoi? Ce serait bien de comprendre pourquoi - ça suffit. Mais regarde:

Eh bien, nous avons compris pourquoi le signe 1 est vrai.

Eh bien, c'est encore plus simple ! Traçons à nouveau une diagonale.

Ce qui signifie:

Et est aussi facile. Mais différent!

Moyens, . Ouah! Mais aussi - unilatéral interne à une sécante !

Par conséquent, le fait que signifie cela.

Et si vous regardez de l'autre côté, alors ils sont internes à sens unique à une sécante ! Et donc.

Vous voyez comme c'est génial ? !

Et encore tout simplement :

Exactement le même, et.

Faites attention: si vous avez trouvé au moins un signe d'un parallélogramme dans votre problème, alors vous avez exactement parallélogramme et vous pouvez utiliser tout le monde Propriétés d'un parallélogramme.

Pour plus de clarté, regardez le schéma :

Propriétés des quadrilatères. Rectangle.

Propriétés du rectangle :

Le point 1) est assez évident - après tout, le signe 3 () est simplement rempli

Et point 2) - très important. Alors prouvons que

Donc, sur deux jambes (et - général).

Eh bien, puisque les triangles sont égaux, leurs hypoténuses sont également égales.

Prouvé cela!

Et imaginez l'égalité des diagonales - caractéristique exactement un rectangle parmi tous les parallélogrammes. C'est-à-dire que l'énoncé suivant est vrai

Voyons pourquoi ?

Donc, (c'est-à-dire les angles du parallélogramme). Mais encore une fois, rappelez-vous que - un parallélogramme, et donc.

Moyens, . Et, bien sûr, il s'ensuit que chacun d'eux Après tout, dans le montant qu'ils devraient donner!

Ici, nous avons prouvé que si parallélogramme tout à coup (!) seront des diagonales égales, alors ce exactement un rectangle.

Mais! Faites attention! C'est à propos de parallélogrammes! Aucun un quadrilatère avec des diagonales égales est un rectangle, et seul parallélogramme!

Propriétés des quadrilatères. Rhombe

Et encore une fois la question est : un losange est-il un parallélogramme ou non ?

Avec plein droit - un parallélogramme, car il a et (Rappelez-vous notre signe 2).

Et encore une fois, puisqu'un losange est un parallélogramme, il doit avoir toutes les propriétés d'un parallélogramme. Cela signifie qu'un losange a des angles opposés égaux, les côtés opposés sont parallèles et les diagonales sont bissectées par le point d'intersection.

Mais il y a aussi des propriétés spéciales. Nous formulons.

Propriétés du losange

Pourquoi? Eh bien, puisqu'un losange est un parallélogramme, ses diagonales sont divisées en deux.

Pourquoi? Oui, c'est pourquoi !

En d'autres termes, les diagonales et se sont avérées être les bissectrices des coins du losange.

Comme dans le cas d'un rectangle, ces propriétés sont distinctif, chacun d'eux est aussi le signe d'un losange.

Signes de losange.

Pourquoi donc? Et regarde

Dès lors, et tous les deux ces triangles sont isocèles.

Pour être un losange, un quadrilatère doit d'abord "devenir" un parallélogramme, puis déjà démontrer la caractéristique 1 ou la caractéristique 2.

Propriétés des quadrilatères. Carré

Autrement dit, un carré est à la fois un rectangle et un losange. Voyons ce qui en ressort.

Est-ce clair pourquoi? Carré - losange - la bissectrice de l'angle, qui est égale à. Donc, il se divise (et aussi) en deux angles le long.

Eh bien, c'est assez clair : les diagonales du rectangle sont égales ; les diagonales de losange sont perpendiculaires et, en général, les diagonales de parallélogramme sont divisées par le point d'intersection en deux.

Pourquoi? Eh bien, appliquez simplement le théorème de Pythagore à.

RÉSUMÉ ET FORMULE DE BASE

Propriétés du parallélogramme :

1. Les côtés opposés sont égaux : , .
2. Les angles opposés sont : , .
3. Les angles d'un côté totalisent : , .
4. Les diagonales sont divisées par le point d'intersection en deux : .

Propriétés du rectangle :

1. Les diagonales d'un rectangle sont : .
2. Rectangle est un parallélogramme (toutes les propriétés d'un parallélogramme sont remplies pour un rectangle).

Propriétés du losange :

1. Les diagonales du losange sont perpendiculaires : .
2. Les diagonales d'un losange sont les bissectrices de ses angles : ; ; ; .
3. Un losange est un parallélogramme (toutes les propriétés d'un parallélogramme sont remplies pour un losange).

Propriétés carrées :

Un carré est à la fois un losange et un rectangle, donc, pour un carré, toutes les propriétés d'un rectangle et d'un losange sont remplies. Ainsi que:

Bon, le sujet est terminé. Si vous lisez ces lignes, alors vous êtes très cool.

Parce que seulement 5% des gens sont capables de maîtriser quelque chose par eux-mêmes. Et si vous avez lu jusqu'au bout, alors vous êtes dans les 5% !

Maintenant la chose la plus importante.

Vous avez compris la théorie sur ce sujet. Et, je le répète, c'est... c'est juste super ! Vous êtes déjà meilleur que la grande majorité de vos pairs.

Le problème c'est que cela risque de ne pas suffire...

Pour quelle raison?

Pour livraison réussie Examen d'État unifié, pour l'admission à l'institut sur le budget et, SURTOUT, à vie.

Je ne vous convaincrai de rien, je dirai juste une chose...

Les personnes qui ont reçu une bonne éducation, gagnent beaucoup plus que ceux qui ne l'ont pas reçu. Ce sont des statistiques.

Mais ce n'est pas l'essentiel.

L'essentiel est qu'ils soient PLUS HEUREUX (il existe de telles études). Peut-être parce que beaucoup plus d'opportunités s'ouvrent devant eux et que la vie devient plus lumineuse ? Je ne sais pas...

Mais pense par toi-même...

Que faut-il pour être sûr d'être meilleur que les autres à l'examen et d'être finalement... plus heureux ?

REMPLISSEZ VOTRE MAIN, RÉSOLVANT LES PROBLÈMES SUR CE SUJET.

À l'examen, on ne vous demandera pas de théorie.

Tu auras besoin de résoudre les problèmes à temps.

Et, si vous ne les avez pas résolus (BEAUCOUP !), vous ferez certainement une erreur stupide quelque part ou ne le ferez tout simplement pas à temps.

C'est comme dans le sport - vous devez répéter plusieurs fois pour gagner à coup sûr.

Trouvez une collection où vous voulez nécessairement avec des solutions analyse détaillée et décidez, décidez, décidez !

Vous pouvez utiliser nos tâches (pas nécessaire) et nous les recommandons certainement.

Afin d'obtenir un coup de main avec l'aide de nos tâches, vous devez aider à prolonger la durée de vie du manuel YouClever que vous lisez actuellement.

Comment? Il y a deux options :

1. Débloquez l'accès à toutes les tâches cachées dans cet article -
2. Débloquez l'accès à toutes les tâches cachées dans les 99 articles du didacticiel - Acheter un manuel - 499 roubles

Oui, nous avons 99 articles de ce type dans le manuel et l'accès à toutes les tâches et à tous les textes cachés qu'ils contiennent peut être ouvert immédiatement.

L'accès à toutes les tâches cachées est fourni pendant toute la durée de vie du site.

En conclusion...

Si vous n'aimez pas nos tâches, trouvez-en d'autres. Ne vous arrêtez pas à la théorie.

« J'ai compris » et « Je sais résoudre » sont des compétences complètement différentes. Vous avez besoin des deux.

Trouvez des problèmes et résolvez-les!